Rat in a Maze Problem in Java

In this section, we will discuss the rat in a maze problem in Java. The rat in a maze problem is one of the famous backtracking problems asked in the interviews.

Problem Statement: A maze is provided in the form R * C matrix, where R is the total number of rows, and C is the total number of columns present in the matrix (R may or may not become equal to C). The cell m[0][0] is the source (observe the following diagram). From the source, the rat starts its journey. The rat has to reach cell m[R - 1][C - 1], the destination cell. The rat can only move in the rightward (→) or in the downward (↓) direction from the cell where it is currently present. Also, note that the rat can only move to its adjacent cell. For example from the cell m[0][0], it can move to m[0][1] or m[1][0]. From m[0][0] it cannot move to m[0][2] or m[2][0] directly as cells m[0][2] or m[2][0] is not adjacent to m[0][0].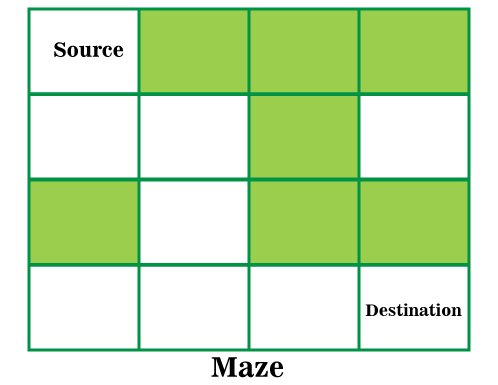

The following is the binary representation of the mentioned maze.

{0, 1, 1, 1} 
{0, 0, 1, 0} 
{1, 0, 1, 1} 
{0, 0, 0, 0}

Here, 0 means that the cell is open, and the rat can enter. 1 means the cell is blocked, and the rat cannot enter.

The following diagram shows the path that the rat can follow to reach the destination.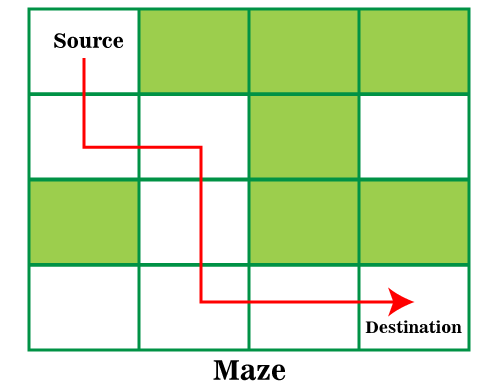

The following is the binary representation of the path shown in the above diagram.

{0, 1, 1, 1} 
{0, 0, 1, 1} 
{1, 0, 1, 1} 
{1, 0, 0, 0}

Only the entries marked using the number 0 represent the path.

Approach

The approach is to create a recursive method. The recursive method will follow a path starting from the source cell and will check whether the path reaches the destination cell or not. If the path is not successful in reaching the destination cell, then backtrack and try out the other paths.

Algorithm

On the basis of the above approach, the following algorithm is written.

Create a result matrix (result[R][C]), and fill each cell of the matrix with 1's.
Create a recursive method that takes the initial matrix, the result matrix, and the current position of the rat (which is (0, 0) initially).
If the position goes out of the matrix or the rat lands in the position is not valid, then return. It is because that path cannot be the correct path. Therefore, no need to proceed further.
Put the value of the cell result[r][c] as 0 and then check whether the current cell is the destination cell or not. If the destination cell is reached, display the result matrix and terminate.
If the destination cell is not reached, then recursively check for the position (r + 1, c) and (r, c + 1).
If the rat cannot reach the destination cell form the position (r, c), then unmark the position or cell (r, c), that is, result[r][c] = 1.

Implementation

Let's see how one can implement the above mathematical formula. Observe the following example.

FileName: RatMazeProblem.java

public class RatMazeProblem 
{

// Size of the maze
static int R;
static int C;

// A utility method to display
// the outcome matrix result[R][C] 
void displaySolution(int result[][])
{
System.out.println("The resultant matrix is: ");
for (int r = 0; r < R; r++) 
{
for (int c = 0; c < C; c++)
{
System.out.print(" " + result[r][c] + " ");
}

System.out.println();
}
}

// A utility method to validate
// whether r, c is the valid index for the R * C maze 
boolean isValid(int maze[][], int r, int c)
{
// if (r, c is outside the maze, then return false
return (r >= 0 && r < R && c >= 0 && c < C && maze[r][c] == 0);
}

// The method solves the rat maze problem with the
// help of Backtracking. It uses the solveMazeUtility()
// method to find the solution to the problem. The method returns false 
// when there is no single valid path from source to destination, otherwise true is 
// returned 

// and displays the path using 0s. Note that there can be more than one path
// from source to destination. However, the method displays one of the feasible ones. 
boolean findPathMaze(int maze[][])
{
int maz[][] = new int[R][C];
for(int r = 0; r < R; r++)
{
for(int c = 0; c < C; c++)
{
maz[r][c] = 1;
}
}


if (solveMazeUtility(maze, 0, 0, maz) == false) 
{
System.out.print("Path from source to destination doesn't exist");
return false;
}

displaySolution(maz);
return true;
}

// A recursive utility method to find the solution of the Maze
// problem 
boolean solveMazeUtility(int maze[][], int r, int c,
		int res[][])
{
// if r, c is the destination, then return true
if (r == R - 1 && c == C - 1 && maze[r][c] == 0) 
{
res[r][c] = 0;
return true;
}

// Check if the maze[r][c] is valid
if (isValid(maze, r, c) == true) 
{
// checking whether the current cell has been the part of the solution path or not
if (res[r][c] == 0)
{
return false;
}

// marking res(r, c) as the part of the solution path
res[r][c] = 0;

// Moving forward in the downward direction 
if (solveMazeUtility(maze, r + 1, c, res))
{
return true;
}
// If moving in downward direction does not provide
// the solution then we move in the rightward direction
if (solveMazeUtility(maze, r, c + 1, res))
{
return true;
}
// If moving in the downward direction does not provide
// the solution then start moving upward 
if (solveMazeUtility(maze, r - 1, c, res))
{
return true;
}
// If moving in the rigtward direction does not provide
// solution then start moving in the left 
if (solveMazeUtility(maze, r, c - 1, res))
{
return true;
}
// if a valid path is not possible from
// the cell (r, c), then mark it as 1
res[r][c] = 1;
return false;
}
return false;
}
// main method
public static void main(String argvs[])
{
// creating an object of the class RatMazeProblem
RatMazeProblem r = new RatMazeProblem();
// creating the maze
int maze[][] = { { 0, 1, 1, 1 },
		       { 0, 0, 1, 0 },
		       { 1, 0, 1, 1 },
		       { 0, 0, 0, 0 } };

R = maze.length;
C = maze[0].length;
r.findPathMaze(maze);
}
}

Output:

The resultant matrix is: 
 0  1  1  1 
 0  0  1  1 
 1  0  1  1 
 1  0  0  0

Time Complexity: The recursion, mentioned in the above example, can run upper-bound 2^(n^2) times. Therefore, the time complexity of the above program is O(2 ^ (n ^ 2)).

Space Complexity: Since we have used an extra matrix (maz[][]). Therefore, the space complexity of the above program is O(n ^ 2).

Next TopicSudoku in Java

← prev next →