Reverse Level Order Traversal in Java

We have already discussed level order traversal here. In this tutorial, we will discuss how to perform the reverse level order traversal in Java. In the input, a binary tree is given to us, and our task is to print the values contained in various children in the reverse level order pattern.

Example 1: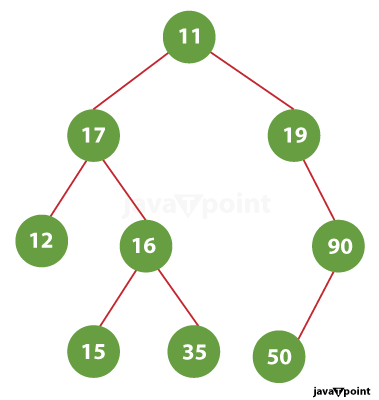

Input:

Output: 15, 35, 50, 12, 16, 90, 17, 19, 11

Example 2:

Input:

Output: 16, 17, 14, 15, 12, 13, 11

Approach: Using Recursion

In the level order traversal, at each level, the values of the nodes are printed from left to right. Now, in this case, we have to recursively traverse all the levels and then print from right to left. However, before doing that, we must know how many levels are there in the binary tree. To find that, all we need to do is to find the height of the tree. The implementation of it is given below.

FileName: ReverseLevelOrderRec.java

Output:

The reverse Level Order traversal of the binary tree is: 
15 35 50 12 16 90 17 19 11 

The reverse Level Order traversal of the binary tree is: 
16 17 14 15 12 13 11

Complexity Analysis: The complexity analysis of the program is O(n²), and the space complexity of the program is O(h), where h is the height of the binary tree.

Approach: Using Queue and Stack

In this approach, we will use a queue and stack. We will first put the root node in the queue, and then its right and left child, if available. After that, pop the parent node and push it into the stack. Now pop the right child, which is now the parent, from the queue and push it into the stack. Push the parent's right child and the left child in the queue. Repeat the above process for the other nodes until the queue becomes empty. Now, using a loop, pop the nodes inserted in the stack and print their value. In this way, we will be able to perform the reverse level order traversal without using recursion.

FileName: BinaryTreeItr.java

Output:

The reverse Level Order traversal of the binary tree is: 
15 35 50 12 16 90 17 19 11 

The reverse Level Order traversal of the binary tree is: 
16 17 14 15 12 13 11

Complexity Analysis: The complexity analysis of the program is O(n²), and the space complexity of the program is O(h), where h is the height of the binary tree.