Tower of Hanoi Program in Java

Three discs with different diameters and a pair of pegs make up the well-known mathematical puzzle known as the Tower of Hanoi. The objective of the puzzle is to move each disc between pegs in accordance with the instructions listed below:

Only move one disc at a time.
We can take the top disc from a stack and place it at the top of another stack.
A smaller disc cannot be stacked on top of another disc.

In this section, we will examine a Java implementation of the Tower of Hanoi issue. We will divide the problem into manageable chunks and offer a thorough description and the related code for each step.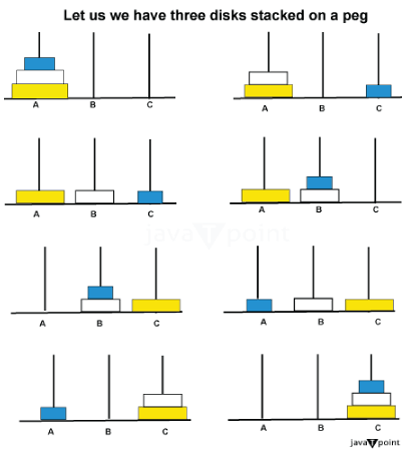

Step 1: Define the Tower of Hanoi Method

Initially, we must develop a recursive solution for the Tower of Hanoi problem. The following parameters should be included in the method:

The number of disks to be moved (n)
The peg or tower from which the disks should be moved (source)
The peg or tower to which the disks should be moved (destination)
An auxiliary peg or tower that can be used during the movement of disks (auxiliary)

Here's the method signature:

public static void towerOfHanoi(int n, char source, char destination, char auxiliary) {
     Main logic
}

Step 2: Define the Base Case

One well-known example of a recursive issue is the Tower of Hanoi problem. For a recursive problem to end, there needs to be a base case. In this case, the base case occurs when there is only one disk to be moved.

if (n == 1) {
    Move disk 1 from " + source + " to " + destination
    return;
}

Step 3: Move n-1 Disks to the Auxiliary Peg

First, we must transfer n-1 discs from the source peg to the auxiliary peg in order to solve the Tower of Hanoi issue for n discs. A recursive call to the towerOfHanoi() method is required for this stage.

Step 4: Move the Largest Disk to the Destination Peg

Once we have moved n-1 disks to the auxiliary peg, we can move the largest disk from the source peg to the destination peg.

Step 5: Move the n-1 Disks from the Auxiliary Peg to the Destination Peg

Finally, we need to move the n-1 disks from the auxiliary peg to the destination peg. Again, this step involves a recursive call to the towerOfHanoi method.

Tower of Hanoi Java Program

TowerOfHanoi.java

public class TowerOfHanoi {
    public static void toh(int n, char source, char destination, char auxiliary) {
        if (n == 1) {
            System.out.println("Move disk 1 from " + source + " to " + destination);
            return;
        }
        toh(n - 1, source, auxiliary, destination);
        System.out.println("Move disk " + n + " from " + source + " to " + destination);
        toh(n - 1, auxiliary, destination, source);
    }
    public static void main(String[] args) {
        // Input: Number of disks
        int n = 3;
        // Define the source, destination, and auxiliary pegs
        char src = 'A';
        char dest = 'C';
        char auxi = 'B';
        // Towers of Hanoi problem main function call
        toh(n, src, dest, auxi);
    }
}

Output:

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

Explanation

The toh() method base case occurs when there's only one disk (n ==1), prompting it to display the action of transferring the disk from the source peg to the destination peg. In the case of more than one disk, the toh() method utilizes recursion to address the Tower of Hanoi problem. It initiates by moving n-1 disks from the source peg to the auxiliary peg, utilizing the destination peg as an auxiliary.

Following that, it transfers the nth disk from the source peg to the destination peg. Finally, the method recursively handles the n-1 disks, moving them from the auxiliary peg to the destination peg while employing the source peg as the auxiliary.

Next TopicTwo Types of Streams Offered by Java

← prev next →