Create A Tree of Coprime in JavaA binary tree is given whose edges are undirected and whose nodes are connected. Also, the tree is not cyclic. The binary tree is made up of t nodes that are numbered from 0 to t - 1 and have exactly t - 1 edge. Every node of the tree contains some value. The 0th node is the root node of the tree. The binary tree is represented using arrays. One array is nodeArr[] which shows the value associated with every node. Another array is edgeArr[][], which is two-dimensional. nodeArr[j] shows the value of the j-th node and edgeArr[j] = [pj, qj] shows that an edge exists between pth node and the qth node. Our task is to create and print an array of the size t, which is ansArr[] in our case, such that ansArr[i] shows the valid ancestor of the ith node. Valid ancestor means an ancestor or node which is nearest to the ith node such that the greatest common factor of the value of the ancestor node and the ith node is 1, i.e., both the values have to be coprime. For simplicity, it is assumed that the value of the nodes of the binary tree is always less than or equal to 50. Example 1:Input: nodeArr[] = {12, 13, 13, 12}, edgeArr[][] = {{0, 1}, {1, 2}, {1, 3}} 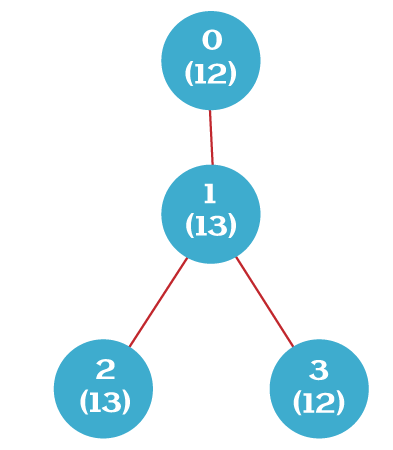
Output: ansArr[] = {-1, 0, 0, 1} Explanation: The node value is mentioned in parentheses (see the above diagram). The root node has no ancestor. Hence, the value of ansArr[0] is -1. The ancestor of node 1 is the root node 0. If we do the gcd of the values of node 0 and node 1, we get gcd(12, 13) = 1, which makes 12 and 13 coprime. Hence, the root node is the valid ancestor of node 1. Therefore, ansArr[1] = 0, as 0th node is the root node. For node 2, the nearest ancestor is node 1, and the gcd of their values are (gcd(13, 13) = 13, which is not 1. Hence, we move one step up, and we reach node 0. Again we compute the gcd of their values. gcd (12, 13) = 1. Hence, 0th node is the valid ancestor of node 2. Therefore, ansArr[2] = 0. For node 3, the nearest ancestor is node 1, and the gcd of their values are coprime as gcd(13, 12) = 1. Thus, the valid ancestor for node 3 is node 1. Hence, ansArr[3] = 1. Example 2:Input: nodeArr[] = {15, 16, 10, 12, 13, 16, 15}, edgeArr[][] = {{0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6}} 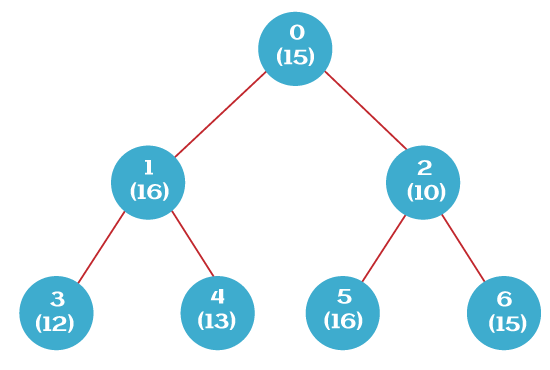
Output: ansArr[] = {-1, 0, -1, 0, 0, 0, -1} Brute Force ApproachThe basic concept is to traverse the whole binary tree. For every node, during the traversal, compute the nearest coprime ancestor. Step 1: Use DFS for traversing the whole binary tree. Step 2: Create a method findGCD() for computing the greatest common divisor of any two numbers. Step 3: For every node, traverse through all of its ancestors from bottom to top to validate whether they are coprime or not. In the worst-case scenario, there will be no ancestor whose gcd (use the method findGCD() for computing the gcd) with the picked node is 1. For those nodes, put -1 in the ansArr. If a valid ancestor is found, put the index of that ancestor in the array ansArr[]. ImplementationObserve the implementation of the above algorithm. FileName: GetCoPrimeSol.java Output: For the first input: For node 0 the valid ancestor is: -1 For node 1 the valid ancestor is: 0 For node 2 the valid ancestor is: 0 For node 3 the valid ancestor is: 1 For the second input: For node 0 the valid ancestor is: -1 For node 1 the valid ancestor is: 0 For node 2 the valid ancestor is: -1 For node 3 the valid ancestor is: -1 For node 4 the valid ancestor is: 1 For node 5 the valid ancestor is: 0 For node 6 the valid ancestor is: -1 Explanation: Since the above program has the nested loop, it has quadratic time complexity. Because of the quadratic time complexity, the above solution is not optimized. We can do the optimization with the help of memorization. Observe the following approach. Optimized ApproachStep 1: Create a graph from the input. Step 2: Precompute the gcd for pair of numbers between 1 and 50 and store them in a (symmetric) matrix: O(50*50). Step 3: Perform a BFS on the graph. While on the BFS, store the parent node of every node encountered in a map, say path, and use the path to perform Backtracking to find the ancestor of the current node that is coprime with the current node using the pre-computed matrix. Step 4: Be sure to use memorization during the Backtracking to avoid the Time Limit being Exceeded. ImplementationObserve the implementation of the above algorithm. FileName: GetCoPrimeSol1.java Output: For the first input: For node 0 the valid ancestor is: -1 For node 1 the valid ancestor is: 0 For node 2 the valid ancestor is: 0 For node 3 the valid ancestor is: 1 For the second input: For node 0 the valid ancestor is: -1 For node 1 the valid ancestor is: 0 For node 2 the valid ancestor is: -1 For node 3 the valid ancestor is: -1 For node 4 the valid ancestor is: 1 For node 5 the valid ancestor is: 0 For node 6 the valid ancestor is: -1 Explanation: Because of the memoization, the time complexity of the above program is O(n * log(n)), where n is the total number of nodes present in the tree. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









