Minimum Lights to Activate Problem in Java

In a Jail, a corridor is provided. The length of the corridor is L units. An array lightArr[] is given, which is also of the size L. The lightArr[] contains only to values 0 & 1. At each unit of the corridor a light is given. If the value at the jth index of the input array lightArr[] is 0, then it means light locate at the jth location is faulty, if the value is 1, then it is not faulty. Note that a faulty light can never be turned on.

All of the lights located in the corridor has the power lightPow. If a light placed is placed at the jth index, then it can illuminate the corridor from (j - lightPow + 1, j + lightPow - 1). The task is to turn on the minimum number of lights that is required to turn onn in order to illuminate the whole corridor. In the beginning all lights are turned off.

Example 1:

Input: lightArr[] = {1, 1, 0, 1, 1}, lightPow = 3

Output: 2

Explanation: Let's see the range of each light.

For the first location light, lightArr[0] is 1. Thus, the range is [0 - 3 + 1, 0 + 3 - 1] = [-2, 2].

For the second location light, lightArr[1] is 1. Thus, the range is [1 - 3 + 1, 1 + 3 - 1] = [-1, 3].

For the third location light, lightArr[2] is 0. Thus, the range can not be computed as the light is faulty.

For the fourth location light, lightArr[3] is 1. Thus, the range is [3 - 3 + 1, 3 + 3 - 1] = [1, 5].

For the fifth location light, lightArr[4] is 1. Thus, the range is [4 - 3 + 1, 4 + 3 - 1] = [2, 6].

The following diagram shows the same.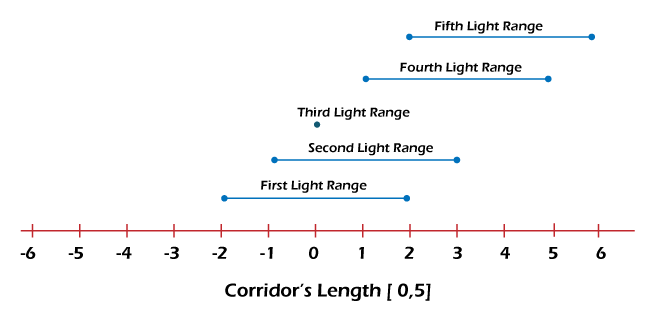

Using the above diagram, it is evident that we can either turn on 1^st and 4^th light, or the 1^st and 5^th light. We can even turn on 2^nd and 4^th light, or 2^nd and 5^th light. Thus, no matter what combination we choose, we atleast need two lights to turn on light up the whole corridor. Hence, the answer is 2.

Example 2:

Input: lightArr[] = {0, 0, 0, 1, 1, 1, 1, 1, 1}, lightPow = 3

Output: Not possible to light the whole corridor

Explanation: It is not possible to light up the first location, even if we turn all the lights.

Using Dyanmic programming

Observe that, when minimum lights are required to illuminate the whole corridor, then minimum lights are also required to illuminate a part of corridor, i.e., minimum lights are required to illuminate the corridor from 0 to 1 unit of corridor, 0 to 2 units of corridor, 0 to 3 units of corridor, and so on. Thus, we can split the bigger problem into smaller problems and find their solution, and use these solution to find the required answer.

Step 1: Create an array (array list will also do) of the size n + 1 (dpArr[] in our case), where n is the total number of elements present in the array lightArr[].

Step 2: Initialize each element with the maximum value of an integer (Integer.MAX_VALUE).

Step 3: Assign 0 value to dpArr[0], as no light is required to illuminate the 0 unit of the corridor.

Step 4: Define dpArr[j] as the value contained in the dpArr[j] is the minimum number of lights required to illuminate the corridor from 0 to j units.

Step 5: Start a loop that iterates over each element of the input array lightArr[]. If the value of an element is 0, then move to the next element. Otherwise, compute the range of the light (say the kth light), and start other loop that iterates on this range. In this range, compute the minimum number of lights that cover the 0 to k units of the corridor. If the value of dpArr[n] is equal to Integer.MAX_VALUE, then it is not possible to illuminate the whole corridor; else it is possible.

Step 6: Return the value of dpArr[n].

Implementation

Observe the implementation of the above algorithm.

FileName: MinLightActivate.java

Output:

For the following lights: 
1 1 0 1 1 
The minimum number of lights to light up the whole corridor is: 2

For the following lights: 
0 0 0 1 1 1 1 1 1 
It is not possible to light up the whole corridor.

Complexity Analysis: We have used nested for-loops for computing the answer. Hence, the time complexity of the program is O(n²). Also, we have used auxiliary array for storing the results, thus the space complexity of the program is O(n), where n is the total number of elements present in the array.

Using Greedy Approach

Every light has the same power B. So, if we greedily start from the left and arrive at a position and pick the rightmost light to cover that position, we will end up getting the minimum no of lights required to cover the whole corridor.

Observe the following algorithm.

Step 1: Take a variable current and consider as the last light from left which is at least covered by one of the tube lights. Initialize current = -1;

Step 2: Start iterating as the following:

For every current position, we find the right most light in the range [ current - lightPow + 1, current + lightPower -1] and then update the current to be this light and repeat the process for other lights.

Implementation: Iterative

Observe the implementation of the above algorithm using the algorithm defined above.

FileName: MinLightActivate1.java

Output:

For the following lights: 
1 1 0 1 1 
The minimum number of lights to light up the whole corridor is: 2

For the following lights: 
0 0 0 1 1 1 1 1 1 
It is not possible to light up the whole corridor.

Complexity Analysis: We have used nested loops for computing the answer. However, the inner for-loop is tweaking the value of the variable i. Thus, the elements of the input array is traversed only once. Hence, the time complexity of the program is O(n). Also, we have not used any extra space for storing the results, thus the space complexity of the program is constant, i.e., O(1).

Implementation: Recursive

We can even use recursion to find the solution. Observe the following program.

FileName: MinLightActivate2.java

Output:

For the following lights: 
1 1 0 1 1 
The minimum number of lights to light up the whole corridor is: 2

For the following lights: 
0 0 0 1 1 1 1 1 1 
It is not possible to light up the whole corridor.

Complexity Analysis: The time complexity is O(n²) and the space complexity is O(n).