Equivalent circuit of an Induction Motor

Stator's Equivalent Circuit:

The stator model of an induction motor consists of a stator phase winding resistance R₁, a stator phase winding leakage reactance X₁. These two components appear to the right of the machine model. The no-load current I₀ is simulated by a pure inductive reactor X₀ taking the magnetizing component I_µ and a non-inductive resistor R₀ carrying the core-loss current I_ω.

Thus,

 I0 = Iµ +Iω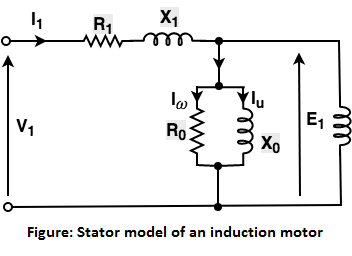

The magnetizing current in the case of the induction motor is higher than the transformer because the air gap of the induction motor causes higher reluctance.

The magnetizing reactance X₀ in an induction motor will have a much smaller value. In a transformer, I₀ is about 2 to 5% of the rated current while in an induction motor it is approximately 25 to 40% of the rated current depending upon the size of the motor.

Rotor's Equivalent Circuit:

It an induction motor, when a 3φ supply is applied to the stator windings, a voltage is induced in the rotor windings of the machine. In general, the higher the relative motion of the rotor and the stator magnetic fields, the higher is the resulting rotor voltage. The maximum relative motion occurs when the rotor is stationary, this condition is called the Standstill condition. This is also known as the locked-rotor or blocked-rotor condition.

If the induced rotor voltage is E₂₀ then the induced voltage at any slip is given by,

  E2s = sE20

The rotor resistance R₂ is constant. It is independent of slip.

The reactance of the induction motor rotor depends upon the inductance of the rotor, voltage frequency, and rotor's current.

If L₂ = inductance of rotor, the rotor reactance is given by

	X2=2πf2 L2
But		f2=sf1
∴		X2=2π sf1 L2=s(2π f1 L2)
Or		X2=sX20

In the above equation, X₂₀ is the standstill reactance of the rotor.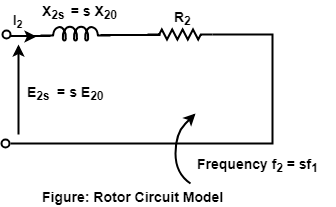

The rotor impedance is given by

Z2s = R2 + jX2s
Or    Z2s = R2 + jsX20

The rotor current per phase is given as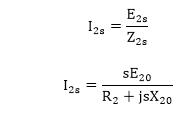

In the circuit drawn above, I₂ is a slip-frequency current produced by a slip-frequency induced voltage sE20 acting in the rotor circuit having an impedance per phase of (R₂ + jsX₂₀).

By dividing both the numerator and the denominator of the above equation by the slip s, we get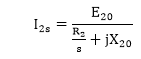

It is to be noted that the magnitude and phase angle of I2s remain the same by this operation.

This equation describes the secondary circuit of a fictitious transformer, one with a constant voltage ratio and with the same frequency of both sides. This fictitious stationary rotor carries the same current as the actual rotating rotor, and, thus produces the same m.m.f wave. This concept of fictitious stationary rotor makes it possible to transfer the secondary impedance to the primary side.