Amortization meaning

What does Amortization mean?

Amortization is defined as a technique used to reduce the debt cost over a period of time. It is primarily used in loan repayments. In case of a loan, it focuses on extending the loan duration to reduce the monthly paid cost.

The Amortization program can be used by financial institutions, moneylenders, etc. to modify the loan schedule based on the specific time and interest rate.

It can also be defined as a method to lower the value of an asset over a period of time.

Let's discuss it in more detail.

Payment structure

Amortization payment is paid regularly. Each payment has two parts: principal and interest; It will always be the sum of principal and interest.

The interest paid every month decreases, while the principal amount increases.

The payment module is quite simple.

Let's consider an example.

Example 1:

Let the loan amount be: 20,000

Rate of Interest: 8%

Tenure to pay the loan amount: 4 months

The payment will be divided into four months (given tenure). The principal and interest for the four months are shown in the below table:

Total interest payable: 334

Total loan amount with interest: 20334

In the beginning, the interest amount is high, while the principal amount is high at the end. It is commonly known as EMI.

Now, let's understand what EMIs are and how to calculate it.

EMI

EMI or Equated Monthly Installment is defined as the lender's monthly amount to a borrower at the specific date of each month. It is the sum of principal and interest so that the loan can be fully paid at the end of the tenure.

According to the personal budget, a person can adjust the money to be paid each month.

The formula to calculate EMI is given below:

The formula to calculate Principal and Amortization are given below: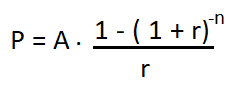

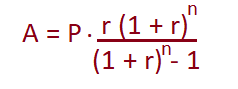
Where,

P = Principle

A = Amortization payment

r = rate of Interest

n = number of payments

The number of payments for 2 years = 2 x 12 months = 24

So, n for 2 years will be 24.

Deferred Interest

The deferred interest is defined as the amount charged for not paying the EMI on time. It is also called as negative Amortization. Such an extra amount is added to the remaining balance, which increases the loan amount. The borrower can also end in a default (failure to meet the loan requirements) mode if he/she cannot immediately pay the installment due to a lack of assets or funds.

Categories

Amortization is based on two categories, which are listed below:

1. Amortization of loans
2. Amortization of Assets

Let's discuss this in detail.

Amortization of loans

Amortization in terms of the loan is defined as the loan payment distribution into monthly installments of EMIs. The total loan amount needs to be paid full until the maturity date. We can calculate amortization using online amortization charts, financial calculators, etc.

The balance left after the first installment is calculated by subtracting the previous month principle amount from the total loan amount. Similarly, the balance after two installments can be calculated by subtracting the sum of the first two principal amounts from the total loan amount.

Let's calculate the balance amount for Example 1.

The table is shown below:

Let's discuss an example to understand the amortization of loans. It is given below:

Example 2:

Let the loan amount be: 400,000

Duration to pay the cost: 5 years

Rate of Interest: 10%

EMI (Equated Monthly Installments): 8499

The Total Interest Payable in five years: 109,929

The total amount with interest: 509,929

Now, let the duration of the same example be 7 years.

Now,

Extended duration: 7 years

EMI: 6640

Total Interest Payable in seven years: 157,800

The total amount with interest: 557,800

Monthly Payments

A particular month's interest payment is calculated by multiplying the outstanding loan balance by the rate of interest and then dividing it by twelve. The formula is given below:

Interest payment = (Outstanding loan balance x rate of interest) /12

The monthly payment due in a particular month is calculated by subtracting the total loan amount by the month's interest payment. The formula is given below:

Monthly payment = Total loan amount - Interest payment.

Monthly payment = Total loan amount - (Outstanding loan balance x rate of interest) /12

Amortization of assets

Amortization is the case of assets is defined as the process of wrapping the cost of an asset throughout the life of that asset. The value of assets is measured in terms of the patent, goodwill, trademarks, or copyright.

The life of assets in which it can be amortized can vary from few years to 40 years. An intangible asset (having no physical value) with indefinite life cannot be amortized.

Let's understand with two examples.

Example 1:

Let's assume that the company ABC has an outstanding loan amount of $4 million. The company ABC repays the principal amount of $400,000 every year. It means that the company has amortized the amount of $400,000 every year.

Example 2:

Let the loan tenure is 3 years.

The loan amount is: $20,000

Rate of Interest is: 6%

Let's calculate the EMI (Equated Monthly Installment) using the formula as discussed above:

EMI = Loan Amount x [r (1 + r) ^n / ((1 + r) ^n - 1)]

Monthly interest rate = Rate of interest/ 12

Monthly interest rate = .06/ 12

Monthly interest rate = 0.005

EMI = $20,000 x [0.005(1.005) ^36 / ((1.005) ^36 - 1)]

EMI = $608.64

Interest payment the first month is calculated using the formula:

Interest payment = (Outstanding loan balance x rate of interest) /12

Interest payment = ($20000 x 0.06) 12

Interest payment = $100

So, the first payment includes:

Interest: $100

Principal: $508.64 = $608.64 - $100

Similarly, further payments are made.