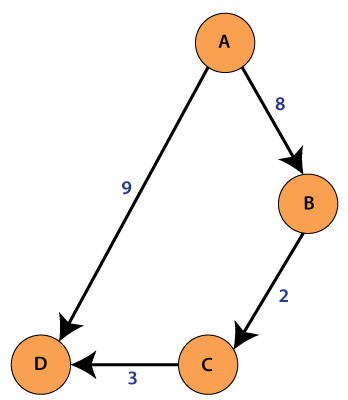
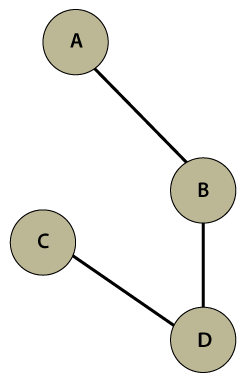
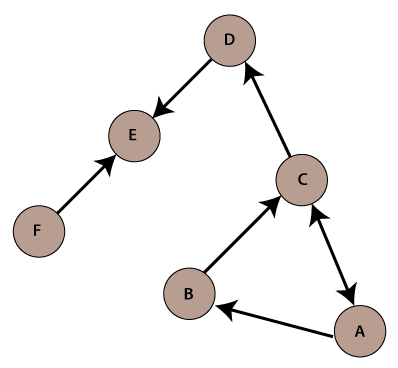
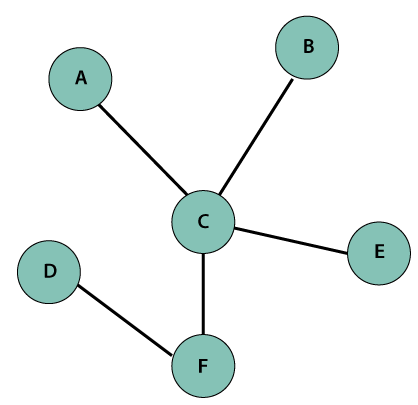
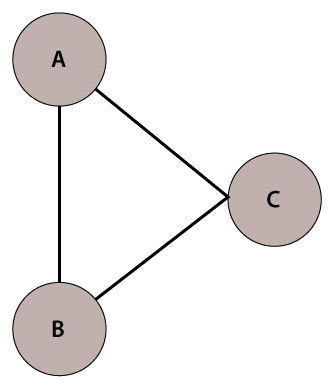
Java Graph

In Java, the Graph is a data structure that stores a certain of data. The concept of the graph has been stolen from the mathematics that fulfills the need of the computer science field. It represents a network that connects multiple points to each other. In this section, we will learn Java Graph data structure in detail. Also, we will learn the types of Graph, their implementation, and traversal over the graph.

Graph

A graph is a data structure that stores connected data. In other words, a graph G (or g) is defined as a set of vertices (V) and edges (E) that connects vertices. The examples of graph are a social media network, computer network, Google Maps, etc.

Each graph consists of edges and vertices (also called nodes). Each vertex and edge have a relation. Where vertex represents the data and edge represents the relation between them. Vertex is denoted by a circle with a label on them. Edges are denoted by a line that connects nodes (vertices).

Graph Terminology

Vertex: Vertices are the point that joints edges. It represents the data. It is also known as a node. It is denoted by a circle and it must be labeled. To construct a graph there must be at least a node. For example, house, bus stop, etc.

Edge: An edge is a line that connects two vertices. It represents the relation between the vertices. Edges are denoted by a line. For example, a path to the bus stop from your house.

Weight: It is labeled to edge. For example, the distance between two cities is 100 km, then the distance is called weight for the edge.

Path: The path is a way to reach a destination from the initial point in a sequence.

Types of Graph

Weighted Graph: In a weighted graph, each edge contains some data (weight) such as distance, weight, height, etc. It denoted as w(e). It is used to calculate the cost of traversing from one vertex to another. The following figure represents a weighted graph.
Unweighted Graph: A graph in which edges are not associated with any value is called an unweighted graph. The following figure represents an unweighted graph.
Directed Graph: A graph in which edges represent direction is called a directed graph. In a directed graph, we use arrows instead of lines (edges). Direction denotes the way to reach from one node to another node. Note that in a directed graph, we can move either in one direction or in both directions. The following figure represents a directed graph.
Undirected Graph: A graph in which edges are bidirectional is called an undirected graph. In an undirected graph, we can traverse in any direction. Note that we can use the same path for return through which we have traversed. While in the directed graph we cannot return from the same path.
Connected Graph: A graph is said to be connected if there exists at least one path between every pair of vertices. Note that a graph with only a vertex is a connected graph.

There are two types of connected graphs.
1. Weekly Connected Graph: A graph in which nodes cannot be visited by a single path is called a weekly connected graph.
2. Strongly Connected Graph: A graph in which nodes can be visited by a single path is called a strongly connected graph.
Disconnected Graph: A graph is said to be disconnected if there is no path between a pair of vertices is called a disconnected graph. A disconnected graph may consist of two or more connected graphs.
Multi Graph: A graph that has multiple edges connecting the same pair of nodes. The following figure represents a multi-graph.
Dense Graph: A graph in which the number of edges is close to the maximal number of edges, the graph is called the dense graph. The following figure represents a dense graph.
Sparse Graph: A graph in which the number of edges is close to the minimal number of edges, the graph is called the sparse graph. It can be a disconnected graph. The following figure represents a sparse graph.

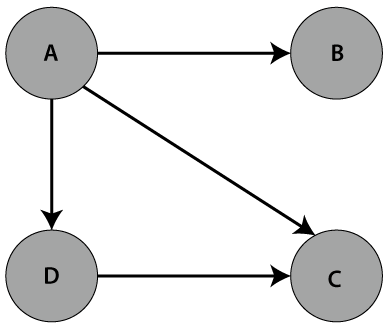
Java Graph Implementation

For the implementation of graphs in Java we will use the Generic class. To create an object of Java Generic class, we use the following syntax:

Remember that, we cannot use primitive type for parameter type.

Let's create a Java program that implements Graph.

GraphImplementation.java

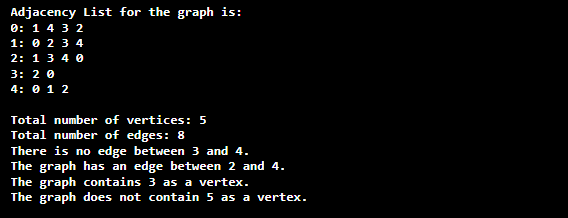
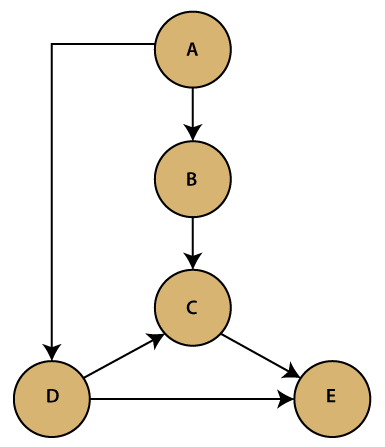
import java.util.*; 
class Graph<T> 
{ 
//creating an object of the Map class that stores the edges of the graph
private Map<T, List<T> > map = new HashMap<>(); 
//the method adds a new vertex to the graph
public void addNewVertex(T s) 
{ 
map.put(s, new LinkedList<T>()); 
} 
//the method adds an edge between source and destination 
public void addNewEdge(T source, T destination, boolean bidirectional) 
{ 
//    
if (!map.containsKey(source)) 
addNewVertex(source); 
if (!map.containsKey(destination)) 
addNewVertex(destination); 
map.get(source).add(destination); 
if (bidirectional == true) 
{ 
map.get(destination).add(source); 
} 
} 
//the method counts the number of vertices
public void countVertices() 
{ 
System.out.println("Total number of vertices: "+ map.keySet().size()); 
} 
//the method counts the number of edges
public void countEdges(boolean bidirection) 
{ 
//variable to store number of edges    
int count = 0; 
for (T v : map.keySet()) 
{ 
count = count + map.get(v).size(); 
} 
if (bidirection == true) 
{ 
count = count / 2; 
} 
System.out.println("Total number of edges: "+ count); 
} 
//checks a graph has vertex or not
public void containsVertex(T s) 
{ 
if (map.containsKey(s)) 
{ 
System.out.println("The graph contains "+ s + " as a vertex."); 
} 
else 
{ 
System.out.println("The graph does not contain "+ s + " as a vertex."); 
} 
} 
//checks a graph has edge or not
//where s and d are the two parameters that represent source(vertex) and destination (vertex)
public void containsEdge(T s, T d) 
{ 
if (map.get(s).contains(d)) 
{ 
System.out.println("The graph has an edge between "+ s + " and " + d + "."); 
} 
else 
{ 
System.out.println("There is no edge between "+ s + " and " + d + "."); 
} 
} 
//prints the adjacencyS list of each vertex
//here we have overridden the toString() method of the StringBuilder class
@Override
public String toString() 
{ 
StringBuilder builder = new StringBuilder(); 
//foreach loop that iterates over the keys
for (T v : map.keySet()) 
{ 
builder.append(v.toString() + ": "); 
//foreach loop for getting the vertices
for (T w : map.get(v)) 
{ 
builder.append(w.toString() + " "); 
} 
builder.append("\n"); 
} 
return (builder.toString()); 
} 
} 
//creating a class in which we have implemented the driver code
public class GraphImplementation
{ 
public static void main(String args[]) 
{ 
//creating an object of the Graph class
Graph graph=new Graph();
//adding edges to the graph
graph.addNewEdge(0, 1, true); 
graph.addNewEdge(0, 4, true); 
graph.addNewEdge(1, 2, true); 
graph.addNewEdge(1, 3, false); 
graph.addNewEdge(1, 4, true); 
graph.addNewEdge(2, 3, true); 
graph.addNewEdge(2, 4, true); 
graph.addNewEdge(3, 0, true); 
graph.addNewEdge(2, 0, true); 
//prints the adjacency matrix that represents the graph
System.out.println("Adjacency List for the graph:\n"+ graph.toString()); 
//counts the number of vertices in the graph 
graph.countVertices(); 
//counts the number of edges in the graph 
graph.countEdges(true); 
//checks whether an edge is present or not between the two specified vertices
graph.containsEdge(3, 4); 
graph.containsEdge(2, 4); 
//checks whether vertex is present or not 
graph.containsVertex(3); 
graph.containsVertex(5); 
} 
}

Output:

Implementation of Directed Graph

DirectedGraph.java

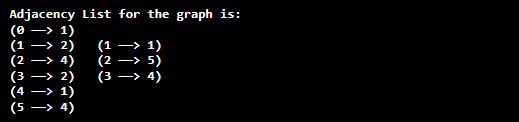
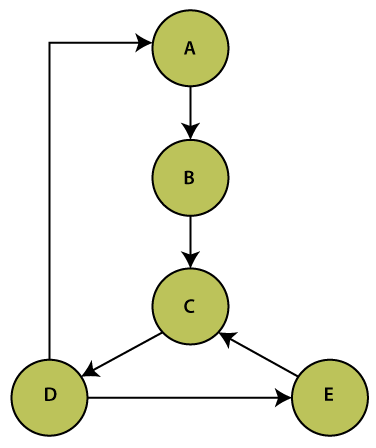
import java.util.*;
//Creating a class named Edge that stores the edges of the graph
class Edge 
{
//the variable source and destination represent the vertices     
int s, d;
//creating a constructor of the class Edge
Edge(int s, int d) 
{
this.s = s;
this.d = d;
}
}
//a class to represent a graph object
class Graph
{
//note that we have created an adjacency list (i.e. List of List)    
List<List<Integer>> adjlist = new ArrayList<>();
//creating a constructor of the class Graph that construct a graph
public Graph(List<Edge> edges)
{
int n = 0;
//foreach loop that iterates over the edge
for (Edge e: edges) 
{
//determines the maximum numbered vertex    
n = Integer.max(n, Integer.max(e.s, e.d));
}
//reserve the space for the adjacency list
for (int i = 0; i <= n; i++) 
{
adjlist.add(i, new ArrayList<>());
}
//adds the edges to the undirected graph
for (Edge current: edges)
{
//allocate new node in adjacency list from source to destination
adjlist.get(current.s).add(current.d);
}
}
//Function to print adjacency list representation of a graph
public static void showGraph(Graph graph)
{
int s = 0;
//determines the size of the adjacency list
int n = graph.adjlist.size();
while (s < n)
{
//prints the neighboring vertices including the current vertex
for (int d: graph.adjlist.get(s)) 
{
System.out.print("Adjacency List for the graph is:");    
//prints the edge between the two vertices    
System.out.print("(" + s + " -- > " + d + ")\t");
}
System.out.println();
//increments the source by 1
s++;
}
}
}
//implementing driver code
public class DirectedGraph
{
public static void main (String args[])
{
//creating a List of edges
List<Edge> edges = Arrays.asList(new Edge(0, 1), new Edge(1, 2), new Edge(2, 4), new Edge(4, 1),new Edge(3, 2), new Edge(2, 5), new Edge(3, 4), new Edge(5, 4), new Edge(1, 1));
// construct a graph from the given list of edges
Graph graph = new Graph(edges);
//prints the adjacency list that represents graph
Graph.showGraph(graph);
}
}

Output:

Implementation of Weighted Graph

WeightedGraph.java

import 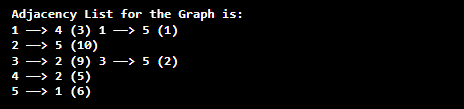java.util.*;
//the class stores the edges of the graph
class Edge 
{
int s, d, w;
//creating a constructor of the class Edge
Edge(int src, int dest, int weight) 
{
this.s = src;
this.d = dest;
this.w = weight;
}
}
//a class to store adjacency list nodes
class Node 
{
int value, weight;
//creating a constructor of the class Vertex
Node(int value, int weight) 
{
this.value = value;
this.weight = weight;
}
//overrides the toString() method
@Override
public String toString() 
{
return this.value + " (" + this.weight + ")";
}
}
//a class to represent a graph object
class Graph
{
//note that we have created an adjacency list (i.e. List of List)    
List<List<Node>> adjlist = new ArrayList<>();
//creating a constructor of the class Graph that creates graph
public Graph(List<Edge> edges)
{
//find the maximum numbered vertex
int n = 0;
//iterates over the edges of the graph
for (Edge e: edges) 
{
//determines the maximum numbered vertex         
n = Integer.max(n, Integer.max(e.s, e.d));
}
//reserve the space for the adjacency list
for (int i = 0; i <= n; i++) 
{
adjlist.add(i, new ArrayList<>());
}
//adds the edges to the undirected graph
for (Edge e: edges)
{
//creating a new node (from source to destination) in the adjacency list 
adjlist.get(e.s).add(new Node(e.d, e.w));
//uncomment the following statement for undirected graph
//adj.get(e.dest).add(new Node(e.src, e.weight));
}
}
//method that prints adjacency list of a graph
public static void printGraph(Graph graph)
{
int src = 0;
int n = graph.adjlist.size();
System.out.printf("Adjacency List for the Graph is: ");    
while (src < n)
{
//for-each loop prints the neighboring vertices with current vertex   
for (Node edge: graph.adjlist.get(src)) 
{
System.out.printf("%d -- > %s\t", src, edge);
}
System.out.println();
//increments the source by 1
src++;
}
}
}
//implementing driver code
public class WeightedGraph
{
public static void main (String args[])
{
//creating a list of edges with their associated weight 
List<Edge> edges = Arrays.asList(new Edge(1, 4, 3), new Edge(4, 2, 5), new Edge(2, 5, 10), new Edge(5, 1, 6), new Edge(3, 2, 9), new Edge(1, 5, 1), new Edge(3, 5, 2));
//creates a graph with the edges declared above
Graph graph = new Graph(edges);
//prints the corresponding adjacency list for the graph
Graph.printGraph(graph);
}
}

Output:

Graph Traversal

Traversal over the graph means visit each and every vertex and edge at least once. To traverse over the graph, Graph data structure provides two algorithms:

Depth-First Search (DFS)
Breadth-First Search (DFS)

Depth-First Search (DFS)

DFS algorithm is a recursive algorithm that is based on the backtracking concept. The algorithm starts from the initial node and searches in depth until it finds the goal node (a node that has no child). Backtracking allows us to move in the backward direction on the same path from which we have traversed in the forward direction.

Let's implement the DFS algorithm in a Java program.

DepthFirstSearch.java

import 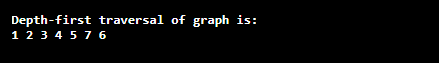java.io.*; 
import java.util.*; 
//creates an undirected graph
class Graph 
{ 
//stores the number of vertices		
private int Vertices;   
//creates a linked list for the adjacency list of the graph 
private LinkedList<Integer> adjlist[]; 
//creating a constructor of the Graph class 
Graph(int count_v) 
{ 
//assigning the number of vertices to the passed parameter	
Vertices = count_v; 
adjlist = new LinkedList[count_v]; 
//loop for creating the adjacency lists
for (int i=0; i<count_v; ++i) 
adjlist[i] = new LinkedList(); 
} 
//method that adds a new edge to the graph
void addNewEdge(int v, int w) 
{ 
adjlist[v].add(w);  // Add w to v's list. 
} 
//logic of the DFS
//traversal starts from the root node 
void traversalDFS(int v, boolean vnodelist[]) 
{ 
//if current node (root node) is visited, add it to the vnodelist 
vnodelist[v] = true; 
System.out.print(v+" "); 
//detrmines the negihboring nodes of the current node
//iterates over the list  
Iterator<Integer> i = adjlist[v].listIterator(); 
while (i.hasNext()) 
{ 
//returns the next element in the iteration and store that element in the variable n	
int n = i.next(); 
if (!vnodelist[n]) 
//calling the function that performs depth first traversal	
traversalDFS(n, vnodelist); 
} 
} 
void DFS(int v) 
{ 
//creates an array of boolean type for visited node 
//initially all nodes are unvisited
boolean visited[] = new boolean[Vertices]; 
//call recursive traversalDFS() function for DFS 
traversalDFS(v, visited); 
} 
}
//implementing driver code
public class DepthFirstSearch
{
public static void main(String args[]) 
{ 
//creates a graph having 10 vertices
Graph g = new Graph(10); 
//add edges to the graph  
g.addNewEdge(1, 2); 
g.addNewEdge(2, 3); 
g.addNewEdge(3, 4); 
g.addNewEdge(4, 5); 
g.addNewEdge(5, 7);
g.addNewEdge(1, 3); 
g.addNewEdge(1, 5); 
g.addNewEdge(5, 5); 
g.addNewEdge(2, 6); 
g.addNewEdge(3, 7);
//print sequencnce in which BFS traversal done 
System.out.println("Depth-first traversal of graph is: ");
//traversal starts from the node 3 (as root node)
g.DFS(1); 
} 
}

Output:

Breadth First Search (BFS)

BFS algorithm is the most common approach to traverse over the graph. The traversal starts from the source node and scans its neighboring nodes (child of the current node). In short, traverse horizontally and visit all the nodes of the current layer. After that, move to the next layer and perform the same.

Let's implement the BFS algorithm in a Java program.

BreadthFirstSearch.java

import java.io.*; 
import java.util.*; 
//creates an undirected graph
class Graph 
{ 
//stores the number of vertices	
private int vertices;  
//creates a linked list for the adjacency list of the graph 
private LinkedList<Integer> adjlist[]; 
//creating a constructor of the Graph class 
Graph(int count_v) 
{ 
//assigning the number of vertices to the passed parameter
vertices = count_v; 
adjlist = new LinkedList[count_v]; 
//loop for creating the adjacency lists
for (int i=0; i<count_v; ++i)         
adjlist[i] = new LinkedList(); 
} 
//method that adds a new edge to the graph
void addNewEdge(int v, int w) 
{ 
adjlist[v].add(w); 
} 
//traversal starts from the root node 
void traversalBFS(int rnode)   
{ 
//creates an array of boolean type for visited node 
//initially all nodes are unvisited
boolean visitednode[] = new boolean[vertices]; 
//creating another list for storing the visited node
LinkedList<Integer> vnodelist = new LinkedList<Integer>(); 
//if current node (root node) is visited, add it to the vnodelist 
visitednode[rnode]=true; 
//inserts the visited node into vnodelist
vnodelist.add(rnode); 
//the while loop executes until we have visited all the nodes
while (vnodelist.size() != 0)  
{ 
//deque an entry from queue and process it  
//the poll() method retrieves and removes the head (first element) of this list
rnode = vnodelist.poll(); 
System.out.print(rnode+" "); 
//detrmines the negihboring nodes of the current node
//iterates over the list 
Iterator<Integer> i = adjlist[rnode].listIterator(); 
while (i.hasNext())
{ 
//returns the next element in the iteration and store that element in the variable n	
int n = i.next(); 
//checks the next node is visited or not
if (!visitednode[n]) 
{ 
//if the above if-statement returns true, visits the node 
visitednode[n] = true; 
//adds the visited node in the vnodelist
vnodelist.add(n); 
} 
} 
} 
} 
}
//implementing driver code
public class BreadthFirstSearch 
{ 
public static void main(String args[]) 
{ 
//creates a graph having 10 vertices
Graph graph = new Graph(10); 
//add edges to the graph  
graph.addNewEdge(2, 5); 
graph.addNewEdge(3, 5); 
graph.addNewEdge(1, 2); 
graph.addNewEdge(2, 4); 
graph.addNewEdge(4, 1); 
graph.addNewEdge(6, 2); 
graph.addNewEdge(5, 6); 
graph.addNewEdge(1, 6); 
graph.addNewEdge(6, 3); 
graph.addNewEdge(3, 1); 
graph.addNewEdge(7, 3); 
graph.addNewEdge(3, 7); 
graph.addNewEdge(7, 5); 
//print sequence in which BFS traversal execute
System.out.println("Breadth-first traversal sequence is: "); 
//root node
graph.traversalBFS(2); 
} 
}

Output:

Next TopicJava Runtime Environment JRE Or JDK Must Be Available

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

Javatpoint Services

JavaTpoint offers too many high quality services. Mail us on h[email protected], to get more information about given services.

Website Designing
Website Development
Java Development
PHP Development
WordPress
Graphic Designing
Logo
Digital Marketing
On Page and Off Page SEO
PPC
Content Development
Corporate Training
Classroom and Online Training
Data Entry

Training For College Campus

JavaTpoint offers college campus training on Core Java, Advance Java, .Net, Android, Hadoop, PHP, Web Technology and Python. Please mail your requirement at [email protected].
Duration: 1 week to 2 week

^{Like/Subscribe us for latest updates or newsletter}