DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
GraphA graph can be defined as group of vertices and edges that are used to connect these vertices. A graph can be seen as a cyclic tree, where the vertices (Nodes) maintain any complex relationship among them instead of having parent child relationship. DefinitionA graph G can be defined as an ordered set G(V, E) where V(G) represents the set of vertices and E(G) represents the set of edges which are used to connect these vertices. A Graph G(V, E) with 5 vertices (A, B, C, D, E) and six edges ((A,B), (B,C), (C,E), (E,D), (D,B), (D,A)) is shown in the following figure. 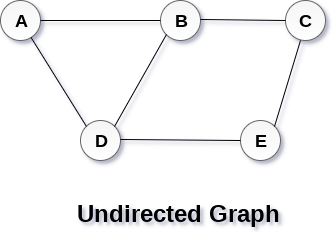
Directed and Undirected GraphA graph can be directed or undirected. However, in an undirected graph, edges are not associated with the directions with them. An undirected graph is shown in the above figure since its edges are not attached with any of the directions. If an edge exists between vertex A and B then the vertices can be traversed from B to A as well as A to B. In a directed graph, edges form an ordered pair. Edges represent a specific path from some vertex A to another vertex B. Node A is called initial node while node B is called terminal node. A directed graph is shown in the following figure. 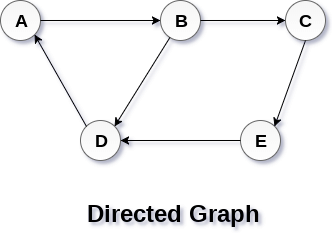
Graph TerminologyPathA path can be defined as the sequence of nodes that are followed in order to reach some terminal node V from the initial node U. Closed PathA path will be called as closed path if the initial node is same as terminal node. A path will be closed path if V0=VN. Simple PathIf all the nodes of the graph are distinct with an exception V0=VN, then such path P is called as closed simple path. CycleA cycle can be defined as the path which has no repeated edges or vertices except the first and last vertices. Connected GraphA connected graph is the one in which some path exists between every two vertices (u, v) in V. There are no isolated nodes in connected graph. Complete GraphA complete graph is the one in which every node is connected with all other nodes. A complete graph contain n(n-1)/2 edges where n is the number of nodes in the graph. Weighted GraphIn a weighted graph, each edge is assigned with some data such as length or weight. The weight of an edge e can be given as w(e) which must be a positive (+) value indicating the cost of traversing the edge. DigraphA digraph is a directed graph in which each edge of the graph is associated with some direction and the traversing can be done only in the specified direction. LoopAn edge that is associated with the similar end points can be called as Loop. Adjacent NodesIf two nodes u and v are connected via an edge e, then the nodes u and v are called as neighbours or adjacent nodes. Degree of the NodeA degree of a node is the number of edges that are connected with that node. A node with degree 0 is called as isolated node.
Next TopicGraph Implementation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









