Count pairs from two BSTs whose sum is equal to given value x
Problem Statement:
Given two BSTs with x1 and x2 distinct nodes and asked to find values of two nodes whose sum is exactly equivalent to value x
Likewise try to implement code for this approach
Approach 1:
To identify pairs in two Binary Search Trees (BSTs), you can perform the following steps without plagiarism concerns:
- For each node value 'a' in BST 1, conduct a search to find the value '(x - a)' in BST 2.
- If the desired value is discovered, increase the count to keep track of the pairs.
Java Implementation of the above mentioned approach
Output:
Explanation:
insert Method:
- The insert method is used to insert a new node with a given value into a BST. It ensures that the nodes are added in the appropriate place based on their values.
countPairsWithSum Method:
- The countPairsWithSum method takes two BSTs (root1 and root2) and a target sum (targetSum) as input.
- It uses a set (valueSet) to store the values from the second BST (root2) and a stack (stack) for iterative traversal.
- The method traverses root2 and populates valueSet with its values, preparing it for later pair counting.
- It then initializes a count to keep track of pairs and traverses root1 to search for values that, when combined with values from valueSet, form pairs with the target sum.
- If a pair is found, the count is incremented.
Approach 2:
- Traverse the first BST (BST 1) from its smallest value to the largest value. This can be accomplished through iterative inorder traversal, which visits nodes in ascending order.
- Simultaneously, traverse the second BST (BST 2) from its largest value to the smallest value. This is achieved through a reverse inorder traversal, visiting nodes in descending order.
- While traversing both BSTs, sum up the values of the corresponding nodes from BST 1 and BST 2 at a given point during the traversal.
- If the sum of these node values equals the target value 'x,' increment a count to keep track of the pairs.
- If the sum is less than 'x,' move to the inorder successor of the current node in BST 1 to potentially increase the sum.
- If the sum is greater than 'x,' move to the inorder predecessor of the current node in BST 2 to potentially decrease the sum.
- Continue these operations until one of the two traversals completes.
This method efficiently finds pairs of nodes in the two BSTs that sum up to the target value 'x' and is a common approach for solving this problem.
Algorithm:
- Initialize count to 0.
- Initialize two empty stacks, stack1 for BST1 and stack2 for BST2.
- Start traversing BST1 in ascending order and BST2 in descending order simultaneously.
- Initialize curr1 to the leftmost node in BST1 (smallest value node).
- Initialize curr2 to the rightmost node in BST2 (largest value node).
- While both curr1 and curr2 are not null or while stack1 and stack2 are not empty, do the following:
- Traverse BST1 in ascending order (inorder) and push nodes onto stack1:
- While curr1 is not null, push curr1 onto stack1, and update curr1 to curr1.left.
- Traverse BST2 in descending order (reverse inorder) and push nodes onto stack2:
- While curr2 is not null, push curr2 onto stack2, and update curr2 to curr2.right.
- Within the loop:
- If stack1 is empty or stack2 is empty, break the loop as one of the traversals is complete.
- Pop the top nodes from stack1 and stack2 (top1 and top2).
- Calculate the sum as sum = top1.value + top2.value.
- If sum is equal to 'x':
- Increment the count by 1.
- If sum is less than 'x':
- Move to the inorder successor of top1 in BST1:
- Set curr1 to top1.right.
- If sum is greater than 'x':
- Move to the inorder predecessor of top2 in BST2:
- Set curr2 to top2.left.
- Return the count as the total number of pairs with a sum equal to 'x' in the two BSTs.
- End of the algorithm.
Java Implementation of the above mentioned approach
Output:
Time Complexity:O(n1+n2)
Space Complexity:O(h1+h2)
Approach 3:
Utilize a recursive strategy to address this problem by traversing BST1, and for each node encountered, calculate the difference (x - root1.data) within BST2, subsequently increasing a counter to keep track of the occurrences.
Java Implementation of the above mentioned approach
Output:
Time Complexity: The code's time complexity is O(n1 * n2) since it involves iterating through each node in BST1 and, for each of those nodes, traversing BST2 to determine if a matching pair with the given difference exists.
Auxiliary Space: The auxiliary space complexity is O(h1 + h2), where h1 represents the height of BST1 and h2 represents the height of BST2. This space is required for the function call stack during the recursive traversal, which increases with the height of the respective trees.
Approach 4: Making use of concept of BST iterator
Two classes InorderSuccessorIterator and InorderPredecessorIterator which serves for inorder and reverseinorder behaviour
Each class will include three functions:
hasNext: Returns true while the traversal is ongoing.
next: Advances the pointer to the next node.
peek: Provides the current node in the ongoing traversal.
After establishing two instances of these classes, execute the iterator while both classes have the next node. Calculate the sum during each iteration. If the sum equals x, proceed by advancing the next pointer of both iterator1 and iterator2. In case the sum is greater than x, increment the next pointer of iterator2; otherwise, increment the next pointer of iterator1 when the sum is less than x.
Java Implementation of the above mentioned approach
Output:
Time Complexity: O(n1 + n2), where n1 and n2 are the total number of nodes in the first and second trees respectively.
Auxiliary Space: O(h1 + h2), where h1 represents the height of the first tree, and h2 represents the height of the second tree.
|
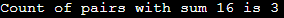
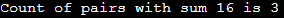
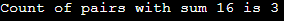
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









