Vertical Traversal of a Binary tree

In this topic, we will see the vertical traversal of a binary tree. For the vertical traversal, we will calculate the horizontal distance. We will assign the horizontal distance to every node, and the horizontal distance could be from any side of the tree. In this case, we will take the left side of the tree from where we will calculate the horizontal distance.

For assigning the horizontal distance to all the node, we will be using the following rules:

For the root node, the value of H_d is equal to 0, i.e., H_d = 0.
For a left child, the value of H_d is equal to the H_d of the parent node minus one, i.e., H_d = H_d - 1.
For the right child, the value of H_dis equal to the H_d of the parent node plus one, i.e., H_d = H_d + 1.

Consider the below tree:

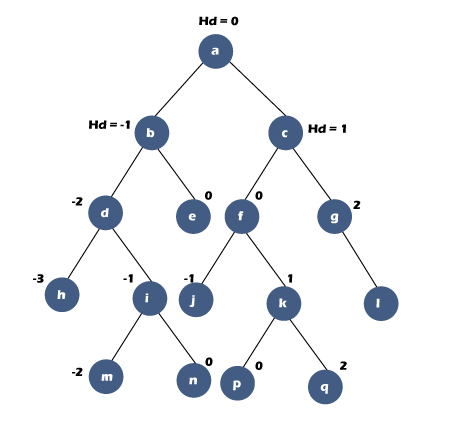
In the above tree, 'a' is the root node, so we will assign the value H_d as 0 to the node. Since 'b' is the left child of node 'a', so rule number 2 will be applied to node 'b'. The H_d value of node 'b' would be equal to 0 minus 1(0-1), i.e., the H_d of node 'b' is equal to -1. The node 'c' is the right child of node 'a', so rule number 3 will be applied to the node 'c'. The H_d value of node 'c' would be equal to 0 plus 1 (0+1), i.e., H_d of node 'c' is equal to 1. The node 'd' is the left child of node 'b', so the H_d value of node 'd' is equal to the H_d value of its parent minus one; therefore, H_d = -1-1 = -2. The node 'e' is the right child of node 'b', so rule number 3 will be applied to this node. The H_d value of 'e' is equal to the H_d value of its parent plus one; therefore, H_d = -1 +1 = 0. The node 'f' is the left child of node 'c'; therefore, the H_d value of 'f' is equal to (1-1) zero. The node 'g' is the right child of node 'c'; therefore, the H_d value of node 'g' is equal to (1+1) = 2. The node 'h' is a left child of node 'd'; therefore, the H_d value of node 'h' is equal to (-2-1) = -3. The node 'i' is the right child of node 'd'; therefore, the H_d value of node 'i' is equal to -1. The node 'j' is the left child of node 'e'; therefore, the H_d value of node 'j' is equal to -1. The node 'k' is the right child of node 'e'; therefore, the H_d value of node 'k' is equal to 1. The node 'l' is the left child of node 'g'; therefore, the H_d value of node 'l' is equal to (2-1) = 1. The node 'm' is the right child of node 'g'; therefore, the H_d value of node 'm' is equal to (2+1) = 3.

The node with the minimum horizontal distance value is 'h', i.e., -3, and the node with a maximum horizontal distance value is 'm', i.e., 3. The nodes that have the same horizontal distance value would exist in the same vertical line.

Now we will create the vertical lines.

The node with a value -3 is 'h', so there exists a vertical line that passes through the node 'h' shown as below:
The node with a value -2 is 'd', so there exists a vertical line that passes through the node 'd' shown as below:
For H_d = -1, there exist three nodes that are 'b', 'i', and 'j', so a vertical line would be created that passes through these three nodes shown as below:
For H_d = 0, there exist two nodes that are 'a', 'e', and 'f', so a vertical line would be created that passes through these three nodes shown as below:
For H_d = 1, there exist three nodes that are 'c', 'k' and 'l', so a vertical line would be created that passes through these three nodes shown as below:
For H_d = 2, there exist a single node, i.e., 'g', so a vertical line passes through the node 'g' shown as below:
For H_d = 3, there exist a single node, i.e., 'm', so a vertical line passes through the node 'm' shown as below:

Algorithm to implement the vertical traversal of a binary tree

This algorithm is a combination of level order traversal and hash table. The following are the steps required for the vertical traversal of a binary tree:

Step 1: Enqueue root.

Step 2: Update H_d distance for root as 0.

Step 3: Add H_d as 0 in a hash table and root as the value.

Step 4: First perform Dequeue operation and then perform the following steps:

Check for the left and right child, and then update H_d in a hash table.
Enqueue the left and right child

Consider the below tree:

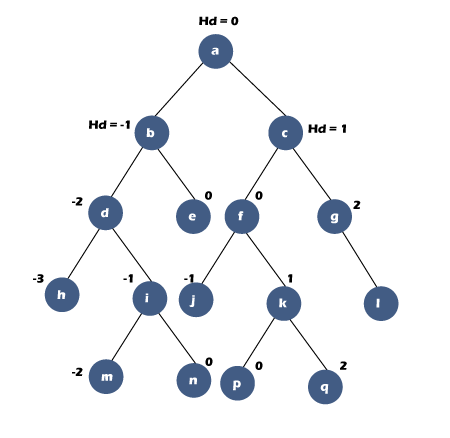
We will use two data structures such as Queue, and hash table to implement the vertical traversal,

We first insert the node 'a' in a queue and update the horizontal distance value of node 'a' as 0. We will also add the H_d of node 'a' and the value in a hash table shown as below:

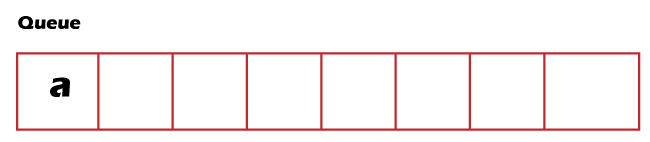
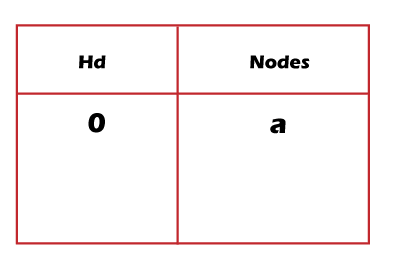
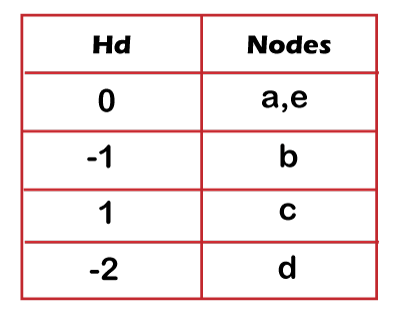
According to Step 4 specified in the algorithm, element 'a' is dequeued from the queue and update the hash table with Hd value of left and right child of node 'a' shown as below:

Once the hash table is updated, we will enqueue the left and right child of node 'a' in a queue shown as below:

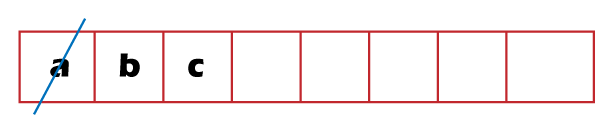
Step 4 is in loop, and it will iterate till the queue does not become empty.

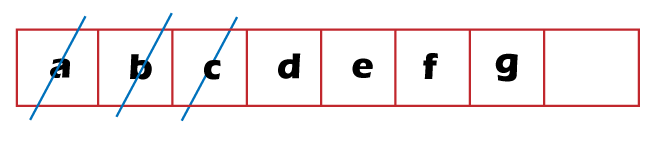
Check whether the queue is empty or not. The queue is not empty, so dequeue the element 'b' from the queue, and check the left and the right child of 'b' node. Since the node 'b' has both left and right child so we will update the hash table with the Hd value of node 'd' and 'e' shown as below:

Once the hash table gets updated, enqueue the nodes 'd' and 'e' in a queue shown as below:

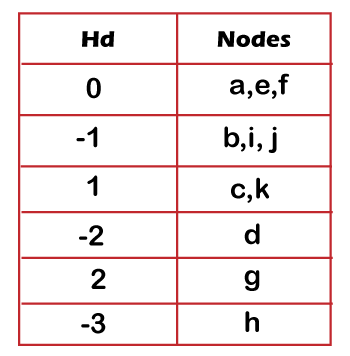
Check whether the queue is empty or not. The queue is not empty so dequeue the element 'c' from the queue, and check the left and right child of 'c' node. Since the node 'c' has both left and right child so we will update the hash table with Hd values of node 'f' and 'g' shown as below:

Once the hash table gets updated, enqueue the nodes 'f' and 'g' in a queue shown as below:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'd' from the queue, and check the left and right child of node 'd'. Since the node 'd' has both left and right child so we will update the hash table with Hd values of 'h' and 'i' shown as below:

Once the hash table gets updated, enqueue the nodes 'h' and 'i' in a queue shown as below:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'e' from the queue, and check the left and right child of node 'e'. Since node 'e' does not have any left and right child so there will be no updation in the hash table:
We will check again whether the queue is empty or not. The queue is not empty so dequeue the element 'f' from the queue, and check the left and right of node 'f'. Since the node 'f' has both left and right child, we will update the hash table with Hd values of 'j' and 'k'.

Once the hash table gets updated, enqueue the nodes 'j' and 'k' in a queue shown as below:

We will check again whether the queue is empty or not. The queue is not empty so dequeue the element 'g' from the queue, and check the left and right of node 'l'. Since the node 'g' has the only right child, we will update the hash table with Hd values of 'l'.

Once the hash table gets updated, enqueue the node 'g' in a queue shown as below:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'h' from the queue, and check the left and right child of node 'h'. Since node 'h' does not have any left and right child so there will be no updation in the hash table:

We will check again whether the queue is empty or not. The queue is not empty so dequeue the element 'i' from the queue, and check the left and right of node 'i'. Since the node 'i' has both left and right child so we will update the hash table with Hd values of 'm' and 'n'.

Once the hash table gets updated, enqueue the nodes 'm' and 'n' in a queue shown as below:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'j' from the queue, and check the left and right child of node 'j'. Since node 'j' does not have any left and right child so there will be no updation in the hash table:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'k' from the queue, and check the left and right child of node 'k'. Since node 'k' has both left and right child so we will update the hash table with Hd values of 'p' and 'q'.

Once the hash table gets updated, enqueue the nodes 'p' and 'q' in a queue shown as below:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'l' from the queue, and check the left and right child of node 'l'. Since node 'l' does not have any left and right child so there will be no updation in the hash table:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'm' from the queue, and check the left and right child of node 'm'. Since node 'm' does not have any left and right child so there will be no updation in the hash table:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'n' from the queue, and check the left and right child of node 'n'. Since node 'n' does not have any left and right child so there will be no updation in the hash table:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'p' from the queue, and check the left and right child of node 'p'. Since node 'p' does not have any left and right child so there will be no updation in the hash table:

Check again whether the queue is empty or not. The queue is not empty so dequeue the element 'q' from the queue, and check the left and right child of node 'q'. Since node 'q' does not have any left and right child so there will be no updation in the hash table: