Merge two binary Max Heaps.Heaps are tree-based data structures that are commonly used to implement priority queues. They allow efficient access to the maximum or minimum element. Sometimes, we must combine two heaps into a single merged heap containing all elements from both. This allows for implementation priority queues that span multiple heaps. This article will examine how to merge two binary max heaps. A max heap has the property that the value of each node is greater than or equal to its children. Merging two such heaps involves recombining their elements into a new max heap containing nodes from both original heaps. We will use a simple O(n) algorithm that optimally merges the structure and elements to create the combined heap. What are Heaps?A heap is a specialized tree data structure that satisfies the "heap property" - the key or value of each node is greater than or equal to (or less than or equal to) the keys of its child nodes. One way to think about a heap is as a "partially ordered binary tree". This means the tree is binary (each node has up to two children), and the order of nodes is based on the heap property, but the overall structure is not fully ordered from top to bottom. Heaps are often implemented using arrays by mapping the tree structure onto index positions. The root node is stored at array index 1, and the children of node i are held at indexes 2i and 2i+1. Unlike a binary search tree, a heap does not guarantee ordering among "siblings" - nodes at the same level. The only guarantee is between parent and child. Heaps are very useful for implementing priority queues because they allow quick access to the minimum or maximum element while also being able to quickly insert and remove parts. So, in summary, a heap is a partially ordered binary tree stored in an array that provides efficient access to the extremum element and flexible insertion/removal. The loose structure, coupled with the heap property, gives heaps their power and popularity. Binary and Binary Max Heap?A binary heap is a heap data structure with two additional constraints - the tree is a complete binary tree, and all levels of the tree are filled except possibly the last level. Being a complete binary tree means that every tree level is filled except for the last level. All nodes are filled in from left to right on the previous level. This property of complete binary trees allows a binary heap to be compactly represented using an array, as described earlier. The first node is stored at array index 1, and a node's left and right children at index i are stored at 2i and 2i+1, respectively. A binary max heap is a binary heap with the additional max-heap property - the key of each node is greater than or equal to the keys of its children. So, in a binary max heap, the largest key is always at the root. The subtree rooted at any node also follows max heap properties. This enables fast access to the maximum value and efficient operations like extract-max, insert, etc. Binary max heaps are a popular way to implement priority queues. In summary, a binary max heap combines three properties:
This combination allows the implementation of efficient priority queues. The max element is easily accessible, inserts and extracts take O(log n) time, and memory usage is compact. Merging two Binary Max HeapsThe goal is to combine two separate binary max heaps into a new binary max heap containing all elements from both heaps. We want to merge both the structure as well as the values. The merged heap should follow max heap properties - its elements should be ordered based on value, with the maximum element at the root. The algorithm involves recursively merging pairs of root nodes:
By recursively comparing and fixing order whenever two nodes are merged, we can combine both the structure and node values to preserve the max heap ordering in the final merged heap. The time complexity is O(n) to merge two heaps containing n elements. This algorithm is asymptotically optimal. 
Output: 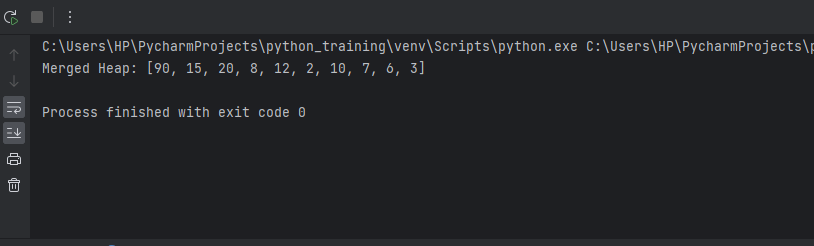
Explanation
More Efficient ApproachThis approach uses a PriorityQueue as an intermediate data structure while merging. A PriorityQueue acts as a max or min heap (by default, min heap). By pushing negative elements, we flip all values so that the PriorityQueue now acts as a max heap, always keeping the maximum element at the top. We use the heap insert and extract-max operations of the PriorityQueue to merge the two input max heaps efficiently, element by element. Finally, we pop elements from the PriorityQueue into a list to return the merged max heap with the proper ordering of elements. The time complexity is O(n) to merge two heaps with total n elements. Using a PriorityQueue avoids writing a custom heapify procedure on the merged array. This makes the logic simpler. The space complexity is O(n) for the merged array of n elements and O(n) for the intermediate PriorityQueue. Output: 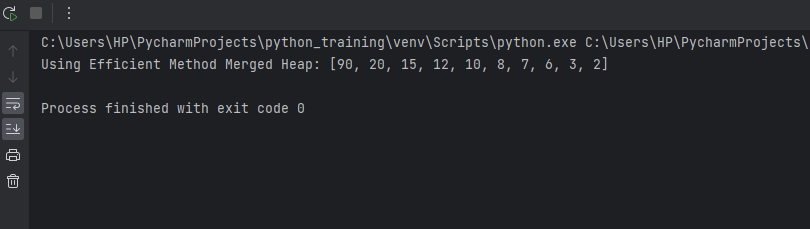
Explanation
10-12. Define input heaps and print merged heap
Next TopicSecure Message Encoding
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









