Segment Tree - Range Minimum Query

In the previous post, we described segment trees with a straightforward example. Another application of Segment Tree is explained in this post when it comes to the Range Minimum Query problem. The issue at hand is as follows:

We have an array called arr[0, 1, n]. Where 0 = qs = qe = n-1, we should be able to efficiently identify the least value from index qs (query start) to qe (query end) 0 <= qs <= qe <= n-1.

Finding the least element in the provided range by running a loop from qs to qe is a straightforward solution. In the worst situation, this solution takes O(n) time.

Making a 2D array with an entry I j] that saves the smallest value in the range arr[i..j] is another option. Preprocessing takes O(n2) time, however it is now possible to find the minimum of a given range in O(1) time. Additionally, this method requires O(n2) additional space, which could be very expensive for big input arrays.

Querying and preprocessing can be done quickly using segment trees. Preprocessing time with a segment tree is O(n), while a range minimum query has an O time complexity (Logn). The additional storage needed for the segment tree is O(n).

Segment tree representation

The elements of the input array are called Leaf Nodes.
Every internal node indicates at least one leaf below it.

Segment Trees are shown as an array representation of a tree. The left child of each node at index I is at index 2*i+1, the right child is at index 2*i+2, and the parent is at index( I - 1) / 2.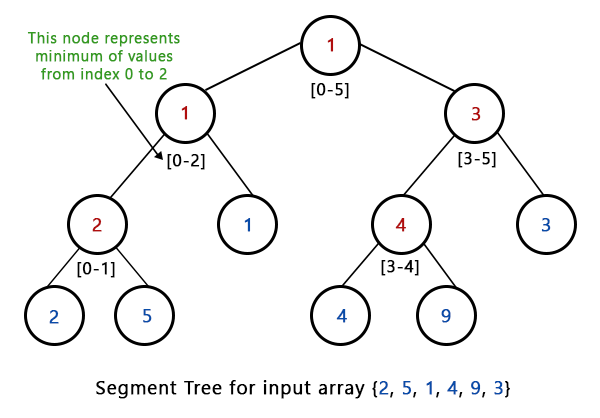

Building a segment tree from an array

We begin by examining the segment arr[0,... n-1]. the current segment is split in half each time (assuming it hasn't already become a segment of length 1), the identical operation is then run on both halves, and we store the minimum value for each such segment in a segment tree node.

Except for the last level, every level of the created segment tree will be fully filled. Additionally, since we consistently split segments into two halves at every level, the tree will be a full binary tree. There will be n-1 internal nodes because the created tree is always a full binary tree with n leaves. Consequently, there will be 2*n - 1 nodes overall.

The segment tree will be log2n in height. Given that the tree is represented using an array and that the relationship between parent and child indexes must be preserved, 2 * 2 log2n - 1 of memory will be allocated for the segment tree.

Find the least value of the specified range.

How to perform a range minimum query utilising the segment tree once it has been built. The algorithm to find the minimum is as follows.

// qs --> query start index, qe --> query end index
int RMQ(node, qs, qe) 
{
   if range of node is within qs and qe
        return value in node
   else if range of node is completely outside qs and qe
        return INFINITE
   else
    return min( RMQ(node's left child, qs, qe), RMQ(node's right child, qs, qe) )
}

C++ Code

The application of the aforementioned strategy is seen below:

// C++ program for range minimum
// query using segment tree
#include <bits/stdc++.h>
using namespace std;

// A utility function to get minimum of two numbers
int minVal(int x, int y) { return (x < y)? x: y; }

// A utility function to get the
// middle index from corner indexes.
int getMid(int s, int e) { return s + (e -s)/2; }

/* A recursive function to get the
minimum value in a given range
of array indexes. The following
are parameters for this function.

	st --> Pointer to segment tree
	index --> Index of current node in the
		segment tree. Initially 0 is
		passed as root is always at index 0
	ss & se --> Starting and ending indexes
				of the segment represented
				by current node, i.e., st[index]
	qs & qe --> Starting and ending indexes of query range */
int RMQUtil(int *st, int ss, int se, int qs, int qe, int index)
{
	// If segment of this node is a part
	// of given range, then return
	// the min of the segment
	if (qs <= ss && qe >= se)
		return st[index];

	// If segment of this node
	// is outside the given range
	if (se < qs || ss > qe)
		return INT_MAX;

	// If a part of this segment
	// overlaps with the given range
	int mid = getMid(ss, se);
	return minVal(RMQUtil(st, ss, mid, qs, qe, 2*index+1),
				RMQUtil(st, mid+1, se, qs, qe, 2*index+2));
}

// Return minimum of elements in range
// from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
int RMQ(int *st, int n, int qs, int qe)
{
	// Check for erroneous input values
	if (qs < 0 || qe > n-1 || qs > qe)
	{
		cout<<"Invalid Input";
		return -1;
	}

	return RMQUtil(st, 0, n-1, qs, qe, 0);
}

// A recursive function that constructs
// Segment Tree for array[ss..se].
// si is index of current node in segment tree st
int constructSTUtil(int arr[], int ss, int se,
								int *st, int si)
{
	// If there is one element in array,
	// store it in current node of
	// segment tree and return
	if (ss == se)
	{
		st[si] = arr[ss];
		return arr[ss];
	}

	// If there are more than one elements,
	// then recur for left and right subtrees
	// and store the minimum of two values in this node
	int mid = getMid(ss, se);
	st[si] = minVal(constructSTUtil(arr, ss, mid, st, si*2+1),
					constructSTUtil(arr, mid+1, se, st, si*2+2));
	return st[si];
}

/* Function to construct segment tree
from given array. This function allocates
memory for segment tree and calls constructSTUtil() to
fill the allocated memory */
int *constructST(int arr[], int n)
{
	// Allocate memory for segment tree

	//Height of segment tree
	int x = (int)(ceil(log2(n)));

	// Maximum size of segment tree
	int max_size = 2*(int)pow(2, x) - 1;

	int *st = new int[max_size];

	// Fill the allocated memory st
	constructSTUtil(arr, 0, n-1, st, 0);

	// Return the constructed segment tree
	return st;
}

// Driver program to test above functions
int main()
{
	int arr[] = {1, 3, 2, 7, 9, 11};
	int n = sizeof(arr)/sizeof(arr[0]);

	// Build segment tree from given array
	int *st = constructST(arr, n);

	int qs = 1; // Starting index of query range
	int qe = 5; // Ending index of query range

	// Print minimum value in arr[qs..qe]
	cout<<"Minimum of values in range ["<<qs<<", "<<qe<<"] "<<
	"is = "<<RMQ(st, n, qs, qe)<<endl;

	return 0;
}

Output:

Minimum of values in range [1, 5] is = 2

Time complexity: The creation of a tree has an O (n) time complexity. There are 2n-1 nodes overall, and the tree creation process only computes each node's value once.
The query's time complexity is O (Logn). We process no more than two nodes at each level to query a range minimum, and the total number of levels is O (Logn).
Auxiliary Space: n additional room has been taken, therefore,O(N)

Next TopicSegment Tree - Sum of given Range

← prev next →