Properties of tree in data structureIntroductionIn a binary tree, which is a hierarchical data structure consisting of nodes, each node has two children: the left child and the right child. The topmost node of the tree is called the root node and serves as the starting point for traversing the tree. Nodes without any children are known as leaves, while nodes with only one child are called interior nodes. Each node in a binary tree has a value that is greater than or equal to the values in its left subtree and less than or equal to the values in its right subtree. This ordering characteristic facilitates efficient search, insertion, and deletion operations on the tree.The length of the longest path from the root to a leaf determines the depth of the tree, which is used to determine a node's level. A binary tree's balance factor is important for preserving efficiency since balanced trees make sure that the height always remains logarithmic in relation to the number of nodes. These characteristics work together to increase binary trees' adaptability and efficiency in a variety of settings, such as search algorithms, expression parsing, and hierarchical data representation. Basic Tree Concepts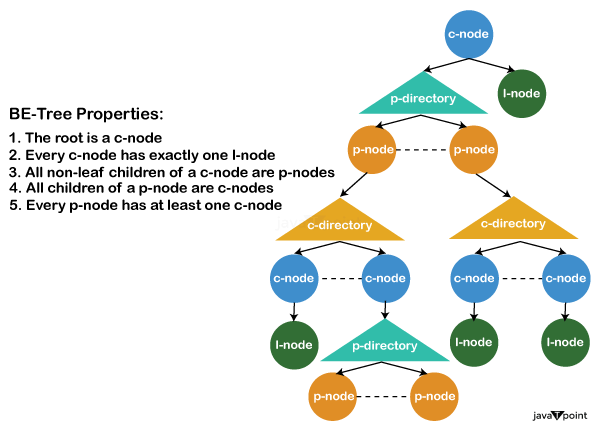
Edges and NodesThe concepts of nodes and edges are the foundation of any tree structure. As the basic building components, think of nodes as intersections in a road network. Each node has data and has the potential to connect to other nodes via edges, producing the tree's branches. Nodes act as storage spaces for information, while edges show the connections or links between these storage spaces. Internal nodes, Leaves, and the RootRoot
Leaves
Internal Nodes
Parent, Child, and SiblingsParent and Child Relationships
Siblings
Types of TreesThere are many kinds of trees in computer science, each suited to particular requirements and uses. For effective problem-solving and algorithm creation, it is crucial to understand the properties and application cases of these various tree architectures. Binary TreeEach node in a binary tree, essentially a data structure, can have at most two children, commonly referred to as a left child and a right child. For more complex tree data structures, this hierarchical structure is proof. Using a straightforward Python function, let's explore the origins of binary trees. Code Output: 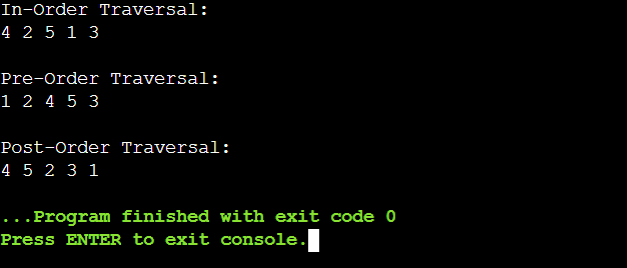
Binary Search Trees (BST)A binary treeis a type of sequencewhere the left subtree of a node consists only of nodes with keys that are smaller than thenode's key, and the right subtree consists only of nodes with keys greater than the node's key. This specific type of binary tree is called a binary search tree (BST). In BSTs, functions like searching, inserting, and deleting nodes are efficient. Code Output: 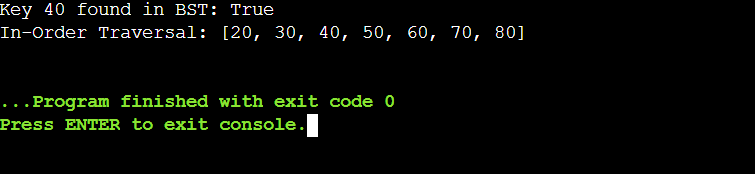
Balancing BSTs: AVL Trees and Red-Black TreesAVL Trees: Self-Balancing Binary Search Trees A particular kind of self-balancing binary search tree is the AVL Tree. The difference in height between any two child subtrees of an AVL Tree is limited to one. Rotations are carried out to restore balance if this property is breached at any point during an insertion or deletion operation. Code Output: 
Balanced Binary Search Trees: Red-Black Trees The red-black tree is another self-balancing binary search tree with unique characteristics. These characteristics guarantee logarithmic time complexity for search, insert, and delete operations while ensuring the tree maintains balance during insertions and removals. Code Output: 
N-ary TreesN-ary Trees are tree architectures in which each node can have multiple offspring. The word "N-ary" denotes that a node can have a maximum of 'N' children, where 'N' is a variable that represents this limit. N-ary trees offer a more adaptable structure than binary trees, which allow just two children per node. Code Output: 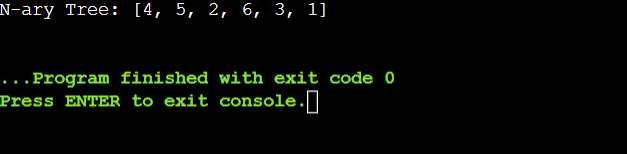
Applications
ConclusionTrees emerge as adaptable tools in the computational toolbox due to their natural capacity to express hierarchical relationships, effectively search and retrieve data, and accommodate specialized applications.The prevalence of trees across numerous fields emphasises how important they are to computer science. Trees are essential for creating effective algorithms and structures, whether used to manage hierarchical relationships in file systems, compress data with Huffman Trees, or optimise search processes. Trees are also essential building blocks in computer science, paving the way for efficient and effective problem-solving due to their adaptability to various applications and their function in preserving balance for optimal performance.
Next TopicRecurrence Relation of Merge Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









