Heap Sort AlgorithmIn this article, we will discuss the Heapsort Algorithm. Heap sort processes the elements by creating the min-heap or max-heap using the elements of the given array. Min-heap or max-heap represents the ordering of array in which the root element represents the minimum or maximum element of the array. Heap sort basically recursively performs two main operations -
Before knowing more about the heap sort, let's first see a brief description of Heap. What is a heap?A heap is a complete binary tree, and the binary tree is a tree in which the node can have the utmost two children. A complete binary tree is a binary tree in which all the levels except the last level, i.e., leaf node, should be completely filled, and all the nodes should be left-justified. What is heap sort?Heapsort is a popular and efficient sorting algorithm. The concept of heap sort is to eliminate the elements one by one from the heap part of the list, and then insert them into the sorted part of the list. Heapsort is the in-place sorting algorithm. Now, let's see the algorithm of heap sort. AlgorithmBuildMaxHeap(arr) MaxHeapify(arr,i) Working of Heap sort AlgorithmNow, let's see the working of the Heapsort Algorithm. In heap sort, basically, there are two phases involved in the sorting of elements. By using the heap sort algorithm, they are as follows -
Now let's see the working of heap sort in detail by using an example. To understand it more clearly, let's take an unsorted array and try to sort it using heap sort. It will make the explanation clearer and easier. 
First, we have to construct a heap from the given array and convert it into max heap. 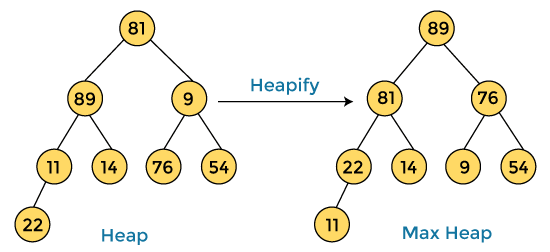
After converting the given heap into max heap, the array elements are - 
Next, we have to delete the root element (89) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap. 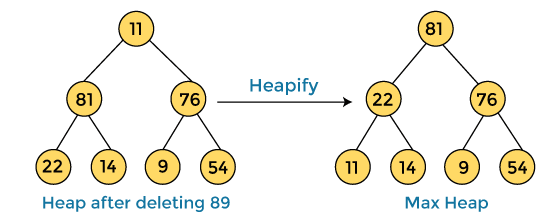
After swapping the array element 89 with 11, and converting the heap into max-heap, the elements of array are - 
In the next step, again, we have to delete the root element (81) from the max heap. To delete this node, we have to swap it with the last node, i.e. (54). After deleting the root element, we again have to heapify it to convert it into max heap. 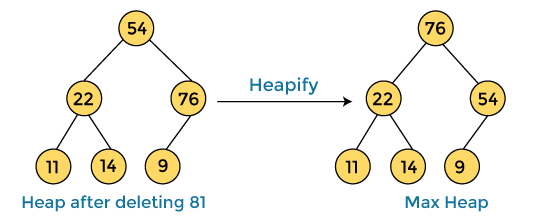
After swapping the array element 81 with 54 and converting the heap into max-heap, the elements of array are - 
In the next step, we have to delete the root element (76) from the max heap again. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap. 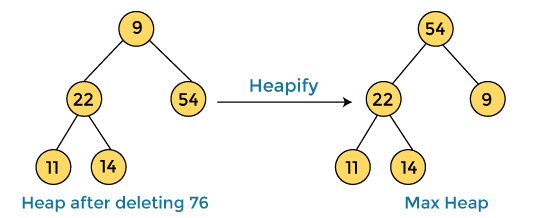
After swapping the array element 76 with 9 and converting the heap into max-heap, the elements of array are - 
In the next step, again we have to delete the root element (54) from the max heap. To delete this node, we have to swap it with the last node, i.e. (14). After deleting the root element, we again have to heapify it to convert it into max heap. 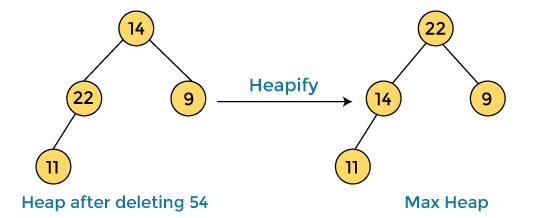
After swapping the array element 54 with 14 and converting the heap into max-heap, the elements of array are - 
In the next step, again we have to delete the root element (22) from the max heap. To delete this node, we have to swap it with the last node, i.e. (11). After deleting the root element, we again have to heapify it to convert it into max heap. 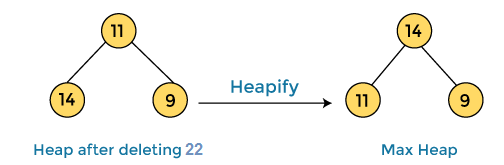
After swapping the array element 22 with 11 and converting the heap into max-heap, the elements of array are - 
In the next step, again we have to delete the root element (14) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap. 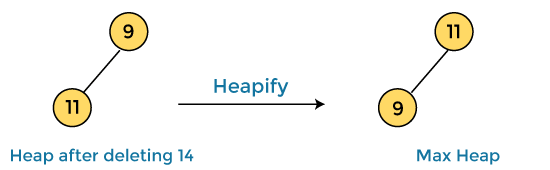
After swapping the array element 14 with 9 and converting the heap into max-heap, the elements of array are - 
In the next step, again we have to delete the root element (11) from the max heap. To delete this node, we have to swap it with the last node, i.e. (9). After deleting the root element, we again have to heapify it to convert it into max heap. 
After swapping the array element 11 with 9, the elements of array are - 
Now, heap has only one element left. After deleting it, heap will be empty. 
After completion of sorting, the array elements are - 
Now, the array is completely sorted. Heap sort complexityNow, let's see the time complexity of Heap sort in the best case, average case, and worst case. We will also see the space complexity of Heapsort. 1. Time Complexity
The time complexity of heap sort is O(n logn) in all three cases (best case, average case, and worst case). The height of a complete binary tree having n elements is logn. 2. Space Complexity
Implementation of HeapsortNow, let's see the programs of Heap sort in different programming languages. Program: Write a program to implement heap sort in C language. Output 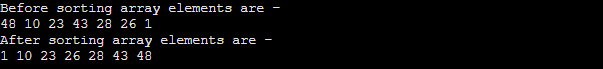
Program: Write a program to implement heap sort in C++. Output 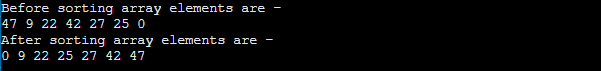
Program: Write a program to implement heap sort in C#. Output 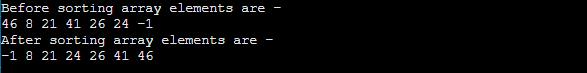
Program: Write a program to implement heap sort in Java. Output 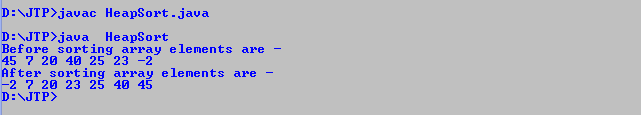
So, that's all about the article. Hope the article will be helpful and informative to you.
Next TopicInsertion Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









