Diameter of a Binary Tree

A tree of binary values is a structure of data that is hierarchical in mathematics and computer science. It consists of nodes, each of which has two children at most, known as the left and right children. These children are binary trees as well. The root is the topmost node in a binary tree, and it serves as the beginning point for navigating the tree.

Following are some key terms and characteristics of binary trees:

1. The root, which is the tree's topmost node, is where all tree traversals start.
2. A node is the name for any component of a binary tree. Data-carrying nodes have a child count of one, two, or zero.
3. Parent: The parent of a child node is a component in the hierarchy which includes a number of children nodes.
4. Child: The node's children are additional nodes that have been intimately associated with it.
5. A leaf node is a node that has never produced any offspring or children.
6. A subtree is a binary hierarchy that is made from a node and every member of its lineage, including children, grandchildren, and so on.
7. The amount of time of the path that extends from the base node through a leaf node determines the circumference of a binary tree. How many edges are there on the steepest downhill route leading to a leaf?
8. Depth: In a binary tree, a node's depth is the distance it takes to get there from the root. The depth of the root node is often defined as 0.

What is a binary search tree (BST)?

It is a binary tree with the extra property that for each node:

1. The values of all nodes in its left subtree are smaller than the node's value.
2. The values of all nodes in its right subtree are greater than the node's value.
3. Binary trees are frequently used in algorithms and data structures such as binary search trees, expression trees, and binary heap storage structures. They are crucial in computer science and programming because they give an efficient way to organize and search data.

Example of Binary Tree

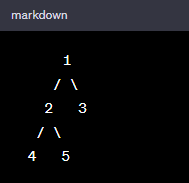
This binary tree contains:

1. The root node's value is 1.
2. The first node is the parent of nodes 2 and 3, which are located on both sides, accordingly.
3. The nodes 4 and 5 are the left and rightmost children of node 2, accordingly.
4. Nodes 4 and 5 are nodes of leaves since they are childless.

This is a straightforward illustration of a binary tree; in actual situations, binary trees can expand and become considerably more complex. Each node can store data, and depending on how nodes are added and organized, the topology of the tree can change. Binary trees are utilized in a variety of applications, such as data storage, searching, and sorting algorithms.

Advantages:

1. Effective Searching: BSTs are great for conducting searches. The binary search property guarantees that the average search time complexity, where n is the number of nodes in the tree, is O(log n).
2. Data that is arranged: BSTs keep data that is arranged. Range queries and ordered data retrieval are made efficient by an in-order traverse of the tree, which results in sorted elements.
3. Effective Insertion and Deletion: Inserting and removing elements is quick and easy with BSTs. These operations typically have a time complexity of O(log n).
4. Balanced Binary Search Trees: Balanced binary search trees like AVL and Red-Black trees make sure that the tree's height stays balanced. It ensures O(log n) time.

Disadvantages:

1. Performance Degradation: In the worst situation, a BST can turn into a linked list when it becomes unbalanced (for example, skewed). In this situation, searching, insertion, and deletion operations are extremely inefficient because of the temporal complexity of O(n).
2. Dependent on Data Order: The order in which the data is inserted affects how effectively BST operations work. When information is added in sorted or nearly sorted order, the tree may become very imbalanced and perform poorly.
3. Lack of Uniqueness: Key uniqueness is not automatically enforced by BSTs. It is possible to insert duplicate keys, and managing duplicates could require further treatment.
4. Balanced BSTs require more complex algorithms to maintain balance despite being effective. Increased coding complexity may result from this complexity.

Binary Tree

A binary tree's diameter is defined as the length of the longest path connecting any two nodes in the tree. This passage may or may not go through the tree's roots. In other terms, it is the number of edges in the longest path in a binary tree between two nodes.

A recursive approach can be used to compute the diameter of a binary tree. A Python code for calculating the diameter of a binary tree is provided below:

This code says:

1. To represent the nodes of the binary tree, we define the TreeNode class.
2. The diameterOfBinaryTree function accepts as input the binary tree's root.
3. We iteratively calculate the height of the left and right subtrees of the current node within the dfs (depth-first search) function.
4. The diameter variable is updated with the largest diameter discovered thus far, which is the sum of the heights of the left and right subtrees.
5. We return the height of the subtree rooted at the current node (1 plus the maximum of the heights of the left and right subtrees) to be utilized in the calculation of the parent node.
6. Finally, we execute the dfs function from the tree's root and return the diameter value, which will be

Conclusion

A binary tree's diameter is defined as the distance between any two of its nodes. This path could pass through the tree's roots or not. How to calculate a binary tree's diameter

1. The left and right subtrees of each node's height (or depth) can be determined recursively.
2. If a longer path passes through a node, the diameter at that node is updated.
3. The binary tree's diameter is the highest possible value among the following:

- The dimension of the opposite subtree. The length of the far left subtree.

- The current component's elevation plus the combined elevations of both the left and right subtrees if this path passes through the current node.

A binary representation of a tree's diameter, a critical statistic for understanding the structure and usefulness of the tree, can be calculated using a recursive method.