Block Swap Algorithm for Array Rotation in Python

Rotating the elements in an array by a given number of positions is an ordinary array operation. The naive way to turn an array is to pop each piece and insert it at the rotated position. However, this requires O(n) swap operations where n is the array length. For large arrays, this is inefficient.

An optimized technique is the block swap algorithm. In this algorithm, the array is divided into blocks, which are swapped as a unit. By swapping contiguous blocks of elements instead of individual components, swap operations can be significantly reduced.

The block swap algorithm utilizes the fact that swapping elements by any multiple of the array length results in the original array. It calculates the greatest common divisor (GCD) of n and r and divides the array into gcd(n,r) blocks. By swapping each block by 1 position gcd(n,r) times, the net result shifts all elements by r positions.

In this article, we will look at how the block swap algorithm works in detail. We will go through the algorithm steps and implement a Python function to rotate an array using the block swap technique.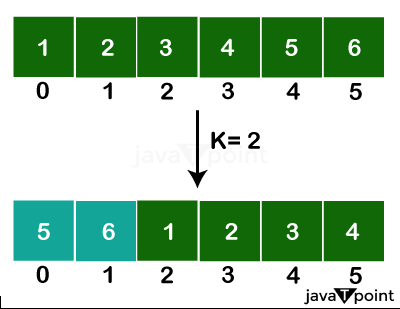

Approach 1: Iterative Approach

Rotating the elements of an array by a given number of positions is an ordinary operation. The naive method of rotating by popping each element and inserting it at the new position requires O(n) swap operations for an array of size n. This can be inefficient for large arrays.

An optimized technique is the block swap algorithm, which divides the array into blocks and swaps the blocks as a unit. By swapping blocks of elements instead of individual components, the algorithm reduces the number of operations needed.

The block swap algorithm works as follows:

1. The array is divided into two blocks - block A from index 0 to d-1 and block B from d to n-1, where d is the rotation amount.
2. The sizes of blocks A and B are compared.
3. The smaller block is swapped with elements from the end of the other block. For example, if A is smaller, it is switched with the last parts of B.
4. The size of the swapped block is decreased, and the process repeats.
5. When the sizes of A and B are equal, the remaining elements are swapped.

This way, the algorithm distributes the swap operations by dividing them into blocks and swapping equal chunks simultaneously.

Python Implementation

Output:

Original Array:
1 2 3 4 5 6 7 
Array after rotating by 2 positions:
3 4 5 6 7 1 2

Explanation

1. swap() function:
   • Accepts array, start indices of two blocks (start1, start2), and block size d
   • Swaps d elements between the two blocks pair-wise
2. block_rotate() function:
   • Check if rotation d is 0 or n; no rotation is needed
   • Initializes i as left block size and j as right block size
   • Enters loop while i not equal to j
     • If i < j, the left block is smaller
       • Call swap() from d-i to d+j-i with size i
       • Reduce j by i
     • Else right block is smaller
       • Call swap() on right block of size j
       • Reduce i by j
     • Final swap() on remaining left block

3. print_array() function:
   • Prints the array elements
4. Main driver code:
   • Define array
   • Take rotation amount d
   • Calculate array size n
   • Print original array
   • Call block_rotate() to rotate the array by d positions
   • Print rotated array

In summary:

• swap() swaps two blocks of size d
• block_rotate() divides the array into two blocks
• Swaps smaller blocks each time
• Reduces the size of the swapped side
• Continues until i = j
• Final swap for remaining elements
• Original and rotated arrays printed

So, the blocks are swapped efficiently by dividing the array into two and swapping equal chunks.

Approach 2: Recursive Approach

The block swap algorithm rotates an array by dividing it into blocks and swapping them. This minimizes the number of swap operations needed compared to rotating elements individually.

An iterative approach was discussed earlier, where the array is split into two blocks, which are swapped in a loop till the blocks are equal in size. However, recursion provides an alternative formulation to implement the same optimized swapping of blocks.

In recursion, a function calls itself to solve more minor instances of the same problem. For array rotation, we can recursively divide the array into smaller blocks, rotate those blocks, and swap the elements to achieve the process.

The recursive approach works as follows:

1. The array is divided into two blocks - block A of size d (rotation positions) and block B of size n-d.
2. These two blocks are swapped to partially rotate the array.
3. The problem is reduced by recurring on either block A or B depending on which one is smaller.
4. In each recursive call, the swapped block is further divided into blocks and swap-recursed until base case is reached.
5. The base cases are when d is 0 or n (no rotation needed) or when n-d = d (array split into two equal halves).
6. By cleverly choosing the block sizes and swapping them recursively, the array is rotated by d positions optimally.

Recursion provides an elegant way to break the problem into smaller subproblems and build the solution bottoms-up. No additional memory is needed as the function stack is used for the recursion. The time complexity remains O(n). We will look at the recursive implementation in detail next.

Output:

Original Array:
1 2 3 4 5 6 7 
Array after rotating by 2 positions:
3 6 4 5 7 1 2

Explanation

1. swap() function is defined to swap the elements between two subarrays within the array. It swaps d elements starting from start with d elements starting from start+end.
2. block_rotate() is the recursive function that performs the rotation.
3. Base cases:
   • If d is 0 or equal to n, no rotation needed so return.
   • If n-d = d, array is split in two equal halves. Swap the halves.
4. If d < n-d:
   • Swap first d elements with last n-d elements.
   • Recursively rotate the first n-d elements.
5. Else if d > n-d:
   • Swap first n-d elements with last d elements.
   • Recursively rotate the last d elements.
6. print_array() function prints the array.
7. Driver code:
   • Creates sample array arr.
   • Calls block_rotate() to rotate arr by d positions.
   • Prints original and rotated array.
8. block_rotate() divides the array in different sized blocks based on d and recursively swaps the blocks while reducing the problem size in each recursion call.

Conclusion

The block swap algorithm provides an efficient way to rotate an array by dividing it into blocks and swapping iteratively. This distributes the swap operations evenly by switching equal-sized chunks at a time. The algorithm reduces the number of swaps from O(n) to O(n/gcd), which can significantly improve large arrays.

In this article, we looked at the detailed working of the iterative block swap approach. The algorithm was implemented in Python by dividing the array into two blocks and swapping the smaller block each time in a loop. This minimizes the number of swap operations while still retaining a linear time complexity. The block swap technique can be applied to rotate arrays in various applications efficiently.