How to insert Strings into an AVL Tree

AVL trees are an advantageous data structure for organizing strings and enabling quick searches, inserts, and deletes. Balancing an AVL tree ensures no branch becomes much longer than others, allowing these operations to be completed in O(log n) time. However, inserting strings presents unique challenges compared to numeric data since string comparison relies on lexicographic rather than numeric order. Correctly inserting strings in an AVL tree requires using the correct comparison logic when searching for the insertion point and then leveraging tree rotations to rebalance the structure. This article will provide clear guidelines on best leveraging AVL trees' self-balancing capabilities to insert strings while maintaining optimal efficiency. We will cover the vital topics of string comparison, insertion logic, height updating, and tree rotations - mastering these techniques is critical to keeping your string AVL tree balanced even after frequent inserts.

What are AVL Trees?

AVL trees are height-balanced binary search trees, allowing efficient search, insertion, and deletion operations. The critical characteristic of an AVL tree is that, for each node, the heights of the left and right subtrees differ by at most 1. This ensures the tree remains roughly balanced during insertions and deletions.

To understand why balancing is necessary, consider a regular binary search tree. As elements are inserted, the tree can become skewed so that one branch becomes much longer. In the worst case, the tree essentially becomes a linked list, requiring O(n) time for search, insert, and delete.

An AVL tree maintains balance through tree rotations after inserts or deletes. Rotation is an operation that rearranges nodes in a tree while maintaining the binary search tree property - left subtree values ≤ current node < right subtree values. Rotations ensure the tree only needs to grow downward by one node before rebalancing resumes.

The operations needed to balance an AVL tree add a slight overhead to insertion and deletion. But they allow these operations to complete in O(log n) time on average. Searches in a balanced AVL tree also take O(log n) time.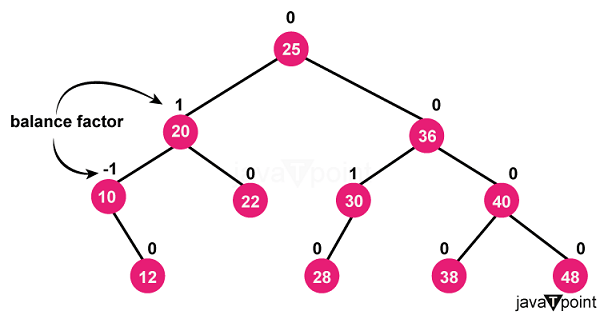

Factors Affecting the Insertion in AVL Trees

Here are the key factors to consider when inserting an element/string into an AVL tree in a point-wise format:

1. Insertion Point

• Traverse the tree comparing each node's value to the insertion value
• Strings use lexicographic ordering for comparison
• Numbers use standard less-than/greater-than comparison
• Traverse left or right based on comparison result
• Reach empty spot for insertion

2. Insert Element

• Insert the new element at the empty node reached

3. Update Heights

• Start from the insertion node and traverse back to the root
• At each node along the path, update its height
• Height = max depth of left and right subtrees + 1

4. Check Balance Factors

• Calculate the balance factor at each node
• Balance factor = height of left subtree - height of right subtree

5. Perform Rotations

• If the balance factor is now -1, 0 or +1 after insertion, rotate to balance
• Rotation types:
  • Left Rotate
  • Right Rotate
  • Left-Right Rotate
  • Right-Left Rotate
• Pick rotation based on the structure of that subtree.

6. Repeat Up the Tree

• Keep checking/fixing the balance going up until the root is reached
• The tree is now rebalanced with the insertion element added

The key challenges are properly comparing strings vs numbers, updating metadata like heights after insertion, and picking the correct rotation at unbalanced nodes to restore balance. Managing these key steps is essential for keeping an AVL tree's efficiency intact after insertions.

Algorithm to Insert String in AVL Tree

Insertion Algorithm

The main steps to insert a string into an AVL tree are:

• Perform standard BST insertion
• Update heights of nodes from updated node to root node
• Rebalance any sub-tree that becomes unbalanced

To insert, start at the root and traverse the tree, comparing the string lexicographically at each node. Keep traversing left/right based on comparison until a null spot is found, and insert the new string there.

After insertion, the tree may need rebalancing. Each node maintains a height property - the max depth of subtrees under it + 1. Update heights and check "balance factors" from the new node towards the root.

The balance factor is: left subtree height - right subtree height

For AVL trees, this must be 1, 0 or -1. If not, rotate that sub-tree.

There are 4 rotation types:

• Left Rotate
• Right Rotate
• Left-Right Rotate
• Right-Left Rotate

Pick rotation based on the structure of the sub-tree at that point.

Example:

Consider inserting "dog" into the tree:

1. Traverse left at cat (d comes before c)

2. Traverse right at the ball (dog comes after b)

3. Insert dog at null node

4. Update heights from the dog up the tree

5. No rotations are needed. The tree is still AVL!

Python Implementation

Output:

Explanation:

1. TreeNode Class
   • Represents a node in the tree
   • Contains key, height, left child and right child pointers
   • key = data being stored
   • height = max depth of subtrees under this node + 1
   • left / right = pointers to the left and right children
2. AVLTree Class
   • Wrapper class to represent the full AVL Tree
   • Contains root node pointer and utility functions
3. get_height()
   • Accepts a TreeNode
   • Returns its height property (max depth of subtrees under it + 1)
   • Used to calculate balance factors
4. get_balance()
   • Accepts a TreeNode
   • Calculates the height difference of its left & right subtrees
   • Formula is: height(left subtree) - height(right subtree)
   • Returns calculated balance factor
5. left_rotate() & right_rotate()
   • These perform the rotations on a subtree
   • Take in the TreeNode that is the root of an unbalanced subtree
   • Return the new root of the subtree after rotation
   • Also, update heights for rotated nodes accordingly
6. insert()
   • The initial public insert method
   • Just calls the private _insert() method doing actual insertion
7. _insert()
   • Handles full insertion logic recursively
   • Base cases: inserts new node when a None node is reached
   • Recursively traverses left/right based on new key
   • After insertion, updates heights & checks balance factors up the path
   • Calls left_rotate(), right_rotate() to fix imbalances
   • Returns final root node pointer back to parent
8. inorder_traversal()
   • Prints keys in sorted ascending order
   • Calls _inorder_traversal() recursively

The core logic lies in the _insert() function and how it leverages the rotate functions to balance subtrees when needed after new keys are inserted. This enables efficient inserts.

Conclusion:

Inserting strings into an AVL tree requires careful handling to maintain balance and efficiency, which are the hallmarks of AVL data structures. Following proper string comparison to locate the insertion point, adding the new node, updating metadata, and performing any necessary rotations ensures strings can be added while keeping the tree optimization intact. When collisions lead to rebalancing, left, right, left-right, or right-left rotations can strategically rearrange nodes to restore balance across all branches. By mindfully accounting for the unique properties of strings and leveraging rotations to counterbalance new additions, AVL trees can support efficient search, insert and delete even with increasingly lengthy strings. Ultimately, combining string handling fundamentals with understanding AVL balanced trees allows your application to scale and perform regardless of the text-based data it absorbs.