Tango Tree Data Structure
Introduction:
In the world of computer science, data structures play a crucial role in organizing and managing information efficiently. Over the years, numerous data structures have been developed to cater to specific needs and challenges. One such innovative addition to this landscape is the Tango Tree data structure. Combining the strengths of two well-known data structures, the Tango Tree introduces a unique approach to solving problems that involve both range queries and point updates.
Understanding Tango Tree:
The Tango Tree is a binary search tree that incorporates two distinct types of nodes: Tango nodes and Leaf nodes. This duality forms the foundation of its structure and balancing mechanism. Tango nodes can have child nodes of both types, while Leaf nodes are the endpoints of the tree with no children. The Tango Tree maintains two primary properties:
- Tango Property: Every internal node (both Tango and Leaf nodes) has at least two children.
- Balancing Property: The height difference between the left and right subtrees of any Tango node is at most one.
The Tango Tree's balancing mechanism is unique: it maintains a balance between Tango and Leaf nodes, ensuring efficient insertion and deletion while avoiding skewed trees. This property contributes to the Tango Tree's logarithmic time complexity for operations.
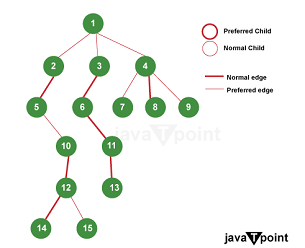
In a Tango tree, each Tango node (internal node) maintains a preferred child and a normal child as part of the Tango view, a virtual structure used to help balance the tree. Each Tango node has a preferred child and a normal child. The choice of preferred and normal child may change during tree operations to maintain the Tango view and the overall balance of the tree.
Leaf nodes (L) do not have preferred or normal child distinctions because they are not involved in maintaining the Tango view or tree balance.
Construction of the Tango Tree:
Constructing a Tango Tree involves a straightforward process that leverages the strengths of the BIT and Segment Tree. It can be broken down into the following steps:
- Initial Data Preparation: Begin by initializing the original data array, which will hold the initial values of the elements you wish to work with.
- Construct BIT and Segment Tree: Build both the Binary Indexed Tree and the Segment Tree based on the given input data array. The BIT will handle point updates, while the Segment Tree will cater to range queries and updates.
- Combine for Tango Tree: The Tango Tree intertwines the BIT and Segment Tree to create a hierarchical structure that allows for efficient querying and updating operations. This is achieved by storing multiple instances of the BIT and Segment Tree, each corresponding to different ranges of elements.
Operations on Tango Tree:
Insertion
The insertion operation in a Tango Tree involves the following steps:
- Locate the appropriate Leaf node for insertion.
- Transform the Leaf node into a Tango node by adding two Leaf children.
- Perform rotations and adjustments to satisfy the Tango and Balancing properties.
Deletion
Deletion in a Tango Tree consists of these steps:
- Locate the node to be deleted.
- If the node is a Tango node, replace it with one of its children and remove the other child.
- If the node is a Leaf node, transform it into a Tango node with two Leaf children.
- Perform rotations and adjustments as necessary to maintain properties.
Searching
Searching in a Tango Tree follows the same principles as a regular binary search tree. Start at the root and traverse left or right based on the comparison between the target value and the current node's value until the target node is found or the traversal reaches a Leaf node.
Implementation:
Now, let's implement the Tango Tree data structure in C++. We'll provide a basic implementation of the Tango Tree operations using classes and methods.
Explanation:
- The tree structure consists of two types of nodes: TangoNode and LeafNode.
- TangoNode represents the internal nodes of the tree, holding an integer value along with pointers to its left and right children. The LeafNode class is a specialized type of node that only holds an integer value.
- The TangoTree class encapsulates the main functionality of the Tango Tree. It contains a private member root, which is a pointer to the root of the tree. The class provides methods for insertion, deletion, and searching of values in the tree.
- The insert method adds a new value to the tree while maintaining the binary search tree property. It includes logic to perform rotations and adjustments, which are fundamental operations in Tango Trees to maintain their balanced structure and improve search efficiency.
- The remove method deletes a value from the tree while ensuring that the tree remains a valid binary search tree. Like the insert method, it also involves rotations and adjustments to maintain balance.
- The search method determines whether a given value exists in the tree. It traverses the tree based on the binary search property, comparing the target value with node values as it traverses down the tree. If the value is found, the method returns true; otherwise, it returns false.
- The main function demonstrates the usage of the TangoTree It creates a TangoTree object and inserts several values into it using the insert method. Then, it searches for specific values using the search method and prints whether each value was found in the tree.
Program Output:

Advantages of the Tango Tree:
- Efficiency: The Tango Tree's primary advantage lies in its efficiency when dealing with problems that require both range queries and point updates. Traditional approaches, such as using only a Segment Tree or a BIT, can lead to suboptimal time complexity for certain operations. The Tango Tree bridges this gap by performing the operations more effectively.
- Versatility: The Tango Tree is a versatile data structure that finds applications in various fields. From solving problems in competitive programming and algorithmic challenges to optimizing database queries, its ability to handle both point updates and range queries makes it a powerful tool.
- Space Optimization: Despite combining two separate data structures, the Tango Tree's memory consumption is often reasonable. This is because it carefully manages the resources required for each substructure and utilizes them only when necessary.
- Elegant Implementation: The Tango Tree's construction might appear complex at first glance, but its elegance lies in how it merges two well-understood concepts into a cohesive whole. Once understood, implementing the Tango Tree becomes straightforward.
Applications of the Tango Tree
The Tango Tree has a wide range of applications across various domains:
- Range-based Queries: Problems involving finding the sum, minimum, maximum, or other statistical measures within a given range benefit from the Tango Tree's combination of efficient range querying from the Segment Tree and point updates from the BIT.
- Offline Queries: In scenarios where you have multiple updates and queries to perform on a set of data, the Tango Tree can handle the problem efficiently, outperforming traditional approaches.
- Dynamic Programming: The Tango Tree's versatility lends itself well to dynamic programming scenarios where you need to maintain some state across multiple iterations or updates.
Conclusion:
The Tango Tree data structure emerges as a remarkable innovation in the realm of computer science, blending the strengths of the Binary Indexed Tree (BIT) and the Segment Tree to create a versatile and efficient solution. Through its elegant combination of these well-established structures, the Tango Tree addresses the limitations of traditional approaches and introduces a new level of efficiency and adaptability to a wide range of computational problems.
In a computing landscape where data structures play a pivotal role in optimizing algorithms and solving complex challenges, the Tango Tree showcases the ingenuity and creativity of researchers and developers.
Its construction, though initially intricate, highlights the potential of merging seemingly disparate concepts into a cohesive whole. This approach not only enhances the capabilities of point updates and range queries but also opens up opportunities for solving novel problems in fields ranging from competitive programming to database management.
One of the Tango Tree's most appealing features is its versatility. By catering to both range queries and point updates, it fills a gap that has often required compromises or intricate workarounds in the past.
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









