Flatten a binary tree into linked list

Introduction

Each node in a binary tree has a maximum of two children, known as the left child and the right child, making it a hierarchical data structure. In order to convert a binary tree into a linked list, the tree nodes must be rearranged in a certain order to make a linear structure. This process is known as "flattening." The objective is to rearrange the nodes of a binary tree so that the tree's structure is maintained while creating a linked list. It is important to create the linked list in a certain order to facilitate simple traversal.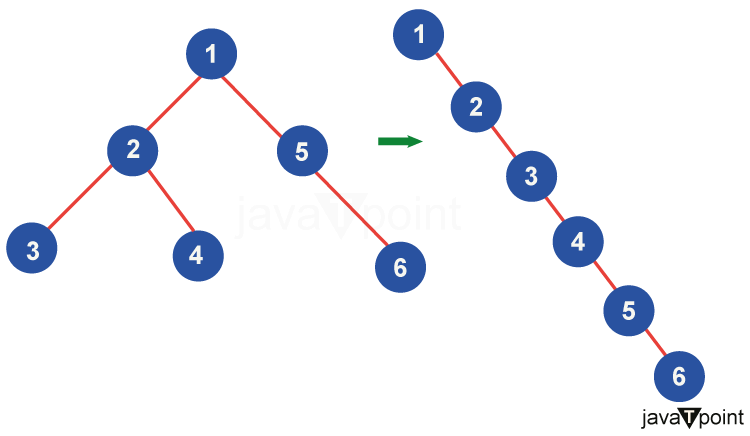

Method 1: Recursion

Using a depth-first traversal approach, the recursive method flattens a binary tree into a linked list by iteratively moving through the tree structure. The function looks for a base case at every stage, making sure to stop when a null node is detected. The approach maintains a reference to the right subtree before flattening the left subtree, which is essential for subsequent reattachment. The procedure is then repeated via a recursive call on the left subtree. The function flattens the left subtree and then moves it to the right of the current node by adjusting pointers. It flattens the original right subtree recursively and proceeds to the end of this new flattened subtree on the right. Because it is recursive, the whole binary tree is inspected, and the nodes are rearranged in a particular sequence to create a linked list. Recursion is elegant because it can decompose a complicated problem into smaller, more manageable subproblems, resulting in more concise and expressive code.

Code

#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};
void flatten(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }
    struct TreeNode* rightSubtree = root->right;
    flatten(root->left);
    root->right = root->left;
    root->left = NULL;
    while (root->right) {
        root = root->right;
    }
    flatten(rightSubtree);
    root->right = rightSubtree;
}
void printList(struct TreeNode* head) {
    while (head != NULL) {
        printf("%d -> ", head->val);
        head = head->right;
    }
    printf("NULL\n");
}
int main() {
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->val = 2;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->val = 5;
    root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->left->val = 3;
    root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->right->val = 4;
    root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->right->val = 6;
    flatten(root);
    printList(root);
    while (root != NULL) {
        struct TreeNode* temp = root;
        root = root->right;
        free(temp);
    }
    return 0;
}

Output:

Code Explanation

Binary Tree Node Definition

Outlines the structure of a binary tree node consisting of three elements: a pointer to the left and right children (left and right) and an integer value (val).

Flatten Function

It is mainly used to convert a binary tree into a linked list.
Accepts as input a pointer to the binary tree's root.

Base Case Verification

The function returns and serves as the recursion's base case if the current node (root) is NULL. By doing this, it is ensured that the recursion ends at the end of each branch.

Save Right Subtree

Retains a reference to the current node's right subtree (root->right). Reattachment at a later time requires this.

Left Flattening Subtree

To flatten the left subtree of the current node, recursively use flatten(root->left) on itself.

Transfer the Left Flattened Subtree to the Right

The flattened left subtree is moved (root->right = root->left) to the right of the current node.
To keep the linked list structure intact, set the left child to NULL.

Proceed to the Right, to the End of the Flattened Subtree

Using a while loop iteratively advances to the right end of the flattened subtree.

Original Right Subtree Flattening

The original right subtree is flattened recursively using flatten(rightSubtree)).

Join the End with the Flattened Right Subtree

(root -> right = rightSubtree) joins the flattened right subtree to the end of the current node.

Print Linked List Function

Defines the printList function, which prints the flattened linked list's values.
Accepts as input a pointer to the linked list's head.

Method 2: Stack

This approach uses an explicit stack to track the nodes as it traverses the graph. The root node is pushed into an empty stack that the algorithm has initialized. A node is removed from the stack at each iteration of a while loop, which runs until the stack is empty. If there is a stack, the right kid is pushed onto it first, and then the left child. Processing of the left child comes first, thanks to this arrangement. The technique simultaneously modifies pointers to link the current node to the appropriate child. The binary tree is flattened depth-first by explicitly managing the traversal order using the stack and modifying pointers accordingly. When recursion is undesirable, this approach is especially helpful because the explicit stack offers an organized approach to handle the traversal and flattening process sequentially.

Code

#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};
struct StackNode {
    struct TreeNode* node;
    struct StackNode* next;
};
struct Stack {
    struct StackNode* top;
};
struct Stack* createStack() {
    struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
    stack->top = NULL;
    return stack;
}
int isEmpty(struct Stack* stack) {
    return stack->top == NULL;
}
void push(struct Stack* stack, struct TreeNode* node) {
    struct StackNode* stackNode = (struct StackNode*)malloc(sizeof(struct StackNode));
    stackNode->node = node;
    stackNode->next = stack->top;
    stack->top = stackNode;
}
struct TreeNode* pop(struct Stack* stack) {
    if (isEmpty(stack)) {
        return NULL;
    }
    struct TreeNode* popped = stack->top->node;
    struct StackNode* temp = stack->top;
    stack->top = stack->top->next;
    free(temp);
    return popped;
}
void flatten(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }
    struct Stack* stack = createStack();
    push(stack, root);
    while (!isEmpty(stack)) {
        struct TreeNode* current = pop(stack);
        if (current->right) {
            push(stack, current->right);
        }
        if (current->left) {
            push(stack, current->left);
        }
        if (!isEmpty(stack)) {
            current->right = stack->top->node;
        }
        current->left = NULL;
    }
}
int main() {
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->val = 2;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->val = 5;
    root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->left->val = 3;
    root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->right->val = 4;
    root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->right->val = 6;
    flatten(root);
    struct TreeNode* current = root;
    while (current != NULL) {
        printf("%d -> ", current->val);
        current = current->right;
    }
    printf("NULL\n");
    while (root != NULL) {
        struct TreeNode* temp = root;
        root = root->right;
        free(temp); }
 return 0;
}

Output:

Code Explanation

Definition of a Binary Tree Node

Outlines the structure of a binary tree node consisting of three elements: a pointer to the left and right children (left and right) and an integer value (val).

Definition of Stack Node

Describes a structure for a stack node that has a pointer to the next stack node (next) and a pointer to a tree node (node).

Definition of Stack

Defines a single component stack structure, which is a pointer to the stack's top (top).

Initialization of Stack

By allocating memory for the stack structure and setting the top pointer to NULL, createStack() initializes an empty stack.

Empty Stack Check

When determining whether a stack is empty, isEmpty() looks to see if the top pointer is NULL.

Push Mechanism

A new node is added to the stack with push(). It creates a new stack node, allocates memory for it, sets its node to the given tree node, and modifies the top pointer appropriately.

Pop Function

pop() takes the top node out of the stack and returns it. It releases memory for the stack node, obtains the tree node of the top node, checks for an empty stack, and modifies the top pointer.

Flattening Mechanism

The primary function flatten() uses an iterative stack-based method to flatten a binary tree's root into a linked list.
After initializing an empty stack and adding the root, iteratively processes nodes while modifying pointers.

Method 3: Iterative without Stack

This technique implicitly simulates the functionality of a stack using a threaded binary tree architecture. It makes use of the Morris Traversal tree traversal method, which threads each node's rightmost child to its successor in the in-order traversal sequence, therefore changing the tree topology. The Morris Traversal is modified for flattening purposes so that it may traverse and flatten the tree at the same time, doing away with the requirement for a stack or other extra data structure. The algorithm moves through the tree quickly and accurately by creating threaded connections between nodes and modifying pointers along the way. This technique is distinguished by its constant space complexity, which renders it a memory-conserving and effective substitute for both recursive and stack-based methods.

Code

#includ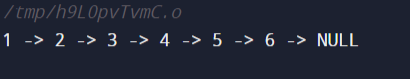e <stdio.h>
#include <stdlib.h>
struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};
void flatten(struct TreeNode* root) {
    while (root != NULL) {
        if (root->left != NULL) {
            struct TreeNode* rightmost = root->left;
            while (rightmost->right != NULL) {
                rightmost = rightmost->right;
            }
            rightmost->right = root->right;
            root->right = root->left;
            root->left = NULL;
        }
        root = root->right;
    }
}
int main() {
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->val = 2;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->val = 5;
    root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->left->val = 3;
    root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->right->val = 4;
    root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->right->val = 6;
    flatten(root);
    struct TreeNode* current = root;
    while (current != NULL) {
        printf("%d -> ", current->val);
        current = current->right;
    }
    printf("NULL\n");
    while (root != NULL) {
        struct TreeNode* temp = root;
        root = root->right;
        free(temp);
    }
    return 0;
}

Output:

Code Explanation

Definition of a Binary Tree Node

Outlines the structure of a binary tree node consisting of three elements: a pointer to the left and right children (left and right) and an integer value (val).

Flatten Function

With the use of the threaded tree traversal method Morris Traversal, the flatten function alters the binary tree in place.
The technique searches the left subtree for the rightmost node for each node that has a left child. This process iterates across the tree nodes.
The left subtree is then attached to the right of the current node, and a threaded connection is formed by moving the right subtree to the right of the rightmost node.
The current node's left child has NULL assigned to it.

Main Function

A sample binary tree is built in the main function.
To use Morris Traversal to flatten the binary tree, the flatten function is called.
Traversing the flattened linked list yields the linearized structure of the original binary tree.

Deallocation of Memory

The allocated memory for the flattened linked list and the binary tree nodes is released by the while loop in the main function. Every node in the linked list is released as it moves through it.

Next TopicGeneral Tree (Each node can have arbitrary number of children) Level Order Traversal

← prev next →