Generating the Maximum Number from Two Arrays

Problem Statement

We are provided with two integer arrays, nums1, and nums2, each representing the digits of two numbers. Additionally, an integer k is given. Our task is to construct the maximum number of length k (where k is less than or equal to the sum of the lengths of nums1 and nums2) from the digits of the two numbers. It is essential to preserve the relative order of the digits within each array.

Java Implementation

Java Approach 1

import java.util.Arrays;
import java.util.Scanner; 
public class MaxNumberGenerator {
    public static int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int n = nums1.length;
        int m = nums2.length;
        int[] ans = new int[k]; 
        for (int i = Math.max(0, k - m); i <= k && i <= n; ++i) {
            int[] candidate = merge(maxArray(nums1, i), maxArray(nums2, k - i), k);
            if (greater(candidate, 0, ans, 0)) ans = candidate;
        }
        return ans;
    }
    private static int[] merge(int[] nums1, int[] nums2, int k) {
        int[] ans = new int[k];
        for (int i = 0, j = 0, r = 0; r < k; ++r)
            ans[r] = greater(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];
        return ans;
    }
    public static boolean greater(int[] nums1, int i, int[] nums2, int j) {
        while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {
            i++;
            j++;
        }
        return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);
    }
    public static int[] maxArray(int[] nums, int k) {
        int n = nums.length;
        int[] ans = new int[k];

        for (int i = 0, j = 0; i < n; ++i) {
            while (n - i + j > k && j > 0 && ans[j - 1] < nums[i]) j--;
            if (j < k) ans[j++] = nums[i];
        }
        return ans;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in); 
        // Input: Lengths of arrays nums1 and nums2, and integer k
        System.out.print("Enter the length of array a: ");
        int len1 = scanner.nextInt();
        int[] nums1 = new int[len1];
        System.out.println("Enter the elements of array a:");
        for (int i = 0; i < len1; i++) {
            nums1[i] = scanner.nextInt();
        }
        System.out.print("Enter the length of array b: ");
        int len2 = scanner.nextInt();
        int[] nums2 = new int[len2];
        System.out.println("Enter the elements of array b:");
        for (int i = 0; i < len2; i++) {
            nums2[i] = scanner.nextInt();
        }
        System.out.print("Enter the value of k: ");
        int k = scanner.nextInt();
        // Calculate and output the max number
        int[] result = maxNumber(nums1, nums2, k);
        System.out.println("The maximum number is: " + Arrays.toString(result)); 
        // Close the scanner
        scanner.close();
    }
}

Output:

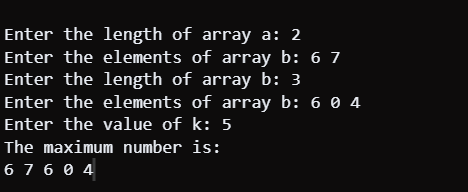
Generating the Maximum Number from Two Arrays

Code Explanation:

The Above Java code implements a Greedy Algorithm to generate the maximum number from two input arrays, nums1 and nums2, with a specified length k.
The maxNumber method explores various combinations of elements from the input arrays, using the merge, maxArray, and greater methods. The merge method merges two subarrays, selecting elements based on the greater method to ensure the resulting array forms the maximum number.
The maxArray method constructs the maximum subarray from a given array, maintaining the highest possible number. The algorithm iteratively makes locally optimal choices at each step, aiming for a globally optimal solution.
The Greedy Algorithm efficiently constructs the maximum number in a manner that is straightforward but may not be the most optimal for large input sizes due to its quadratic time complexity.

Time Complexity:

The time complexity of the algorithm depends on the maxArray, merge, and greater methods.
In the worst case, the maxNumber method iterates over all possible combinations, resulting in a time complexity of O(n^2), where n is the maximum of the lengths of nums1 and nums2.

Space Complexity:

The space complexity is O(k), where k is the specified length of the result array.
Additional space is used for storing candidate arrays and the final result.

Drawbacks:

The drawback of the provided solution lies in its inefficiency for large inputs due to a quadratic time complexity. The algorithm explores all possible combinations of elements from nums1 and nums2, resulting in an O(n^2) time complexity.
As the input sizes increase, the execution time grows significantly, limiting its scalability. There exists a more optimized approach for this problem, suggesting the potential for improved efficiency with alternative algorithms.

Java Approach 2

import java.util.Scanner;
import java.util.Stack;

public class LexicographicallyMax {
    public int[] findLexMax(int[] nums, int k) {
        int n = nums.length;
        Stack<Integer> st = new Stack<>();
        int[] res = new int[k]; 
        int rem = n - k;
        for (int i = 0; i < n; i++) {
            while (!st.isEmpty() && st.peek() < nums[i] && rem > 0) {
                st.pop();
                rem--;
            }
            st.push(nums[i]);
        }
        while (rem > 0) {
            st.pop();
            rem--;
        }
        for (int i = k - 1; i >= 0; i--) {
            res[i] = st.pop();
        }
        return res;
    }
    private static boolean findMax(int[] arr1, int[] arr2, int p1, int p2) {
        while (p1 < arr1.length && p2 < arr2.length) {
            if (arr1[p1] < arr2[p2]) {
                return false;
            } else if (arr1[p1] > arr2[p2]) {
                return true;
            } else {
                p1++;
                p2++;
            }
        }
        return p1 != arr1.length;
    }
    private int[] merge(int[] nums1, int[] nums2, int k) {
        int[] res = new int[k];
        int resIndex = 0;
        int p1 = 0;
        int p2 = 0; 
        while (resIndex < res.length) {
            res[resIndex++] = findMax(nums1, nums2, p1, p2) ? nums1[p1++] : nums2[p2++];
        }
        return res;
    }
    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int[] maxRes = new int[k];
        for (int i = 0; i <= k; i++) {
            int j = k - i;
            if (i <= len1 && (k - i) <= len2) {
                int[] maxLex1 = findLexMax(nums1, i);
                int[] maxLex2 = findLexMax(nums2, j);
                int[] res = merge(maxLex1, maxLex2, k);
                boolean compareRes = findMax(res, maxRes, 0, 0);
                if (compareRes) {
                    maxRes = res;
                }
            }
        }
        return maxRes;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // Input: Lengths of nums1, nums2, and k
        System.out.print("Enter the length of array a: ");
        int len1 = scanner.nextInt();
        int[] nums1 = new int[len1];
        System.out.println("Enter the elements of array a:");
        for (int i = 0; i < len1; i++) {
            nums1[i] = scanner.nextInt();
        }
        System.out.print("Enter the length of array b: ");
        int len2 = scanner.nextInt();
        int[] nums2 = new int[len2];
        System.out.println("Enter the elements of array b:");
        for (int i = 0; i < len2; i++) {
            nums2[i] = scanner.nextInt();
        }
        System.out.print("Enter the value of k: ");
        int k = scanner.nextInt();
        LexicographicallyMax solution = new LexicographicallyMax();
        int[] result = solution.maxNumber(nums1, nums2, k); 
        // Output: Display the result
        System.out.print("The maximum number is: ");
        for (int num : result) {
            System.out.print(num + " ");
        }
        // Close the scanner
        scanner.close();
    }
}

Output:

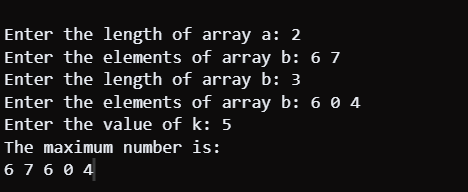
Code Explanation:

The Java code implements a solution to find the lexicographically maximum number by merging subsequences from two arrays, nums1 and nums2, with a specified length k. The algorithm utilizes the findLexMax method to extract the lexicographically maximum subsequence of a given length.
The merge method merges two arrays based on lexicographical comparison, and the maxNumber method explores all possible combinations of subsequences to find the overall lexicographically maximum number.
The algorithm employs a stack to efficiently track the maximum elements. The findMax method compares two subarrays lexicographically. The main method takes user input for array lengths, elements, and k, and then displays the lexicographically maximum result.

Time Complexity:

The maxNumber method explores all possible combinations, leading to a time complexity proportional to the product of k and the sum of array lengths (len1 and len2).
For each combination, the findLexMax method has a time complexity proportional to the sum of array lengths plus k.
The merge and findMax methods contribute additional linear time complexities.

Space Complexity:

The space complexity of the provided solution is O(k). This is primarily attributed to the stack used in the findLexMax method, which grows linearly with the specified length k. Additional constant space is used for variables and temporary arrays..

Drawbacks:

The drawback of the Above solution lies in its reliance on a brute-force approach, exploring all possible combinations to find the lexicographically maximum number. This exhaustive exploration results in a time complexity of O(k * (len1 + len2 + k)), making it inefficient for large inputs.
As the value of k or the lengths of input arrays (nums1 and nums2) increase, the execution time escalates significantly, impacting scalability.
The algorithm lacks optimization techniques that could potentially reduce time complexity. A more sophisticated algorithmic approach or optimization is needed to address the inefficiency and enhance the algorithm's practical usability.

Next TopicHashing and its Applications

← prev next →