Strict Binary Tree

The common non-linear data structure known as a tree. A tree illustrates a hierarchical structure in contrast to other data structures such an array, stack, queue, and linked list, which are linear in nature. A tree's ordering information is irrelevant. Two pointers and nodes make up a tree. The parent node's left and right children are represented by these two pointers. Let's thoroughly comprehend the words used in trees.

The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
Parent Node: A node's parent one is the node that came before it in the tree of nodes.
Child Node: The node that is a node's direct successor is referred to as a node's child node.
Siblings are the children of the same parent node.
Edge: Edge serves as a connecting node between the parent and child nodes.
Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
A node's subtree is the tree that views that specific node as the root node.
Depth: The depth of a node is the separation between it and the root node.
Height: The height of a node is the distance between it and the subtree's deepest node.
The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
Level: In the tree, a level is the number of parents that correspond to a particular node.
Node degree: A node's degree is determined by how many children it has.
A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.

The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
Parent Node: A node's parent one is the node that came before it in the tree of nodes.
Child Node: The node that is a node's direct successor is referred to as a node's child node.
Siblings are the children of the same parent node.
Edge: Edge serves as a connecting node between the parent and child nodes.
Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
A node's subtree is the tree that views that specific node as the root node.
Depth: The depth of a node is the separation between it and the root node.
Height: The height of a node is the distance between it and the subtree's deepest node.
The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
Level: In the tree, a level is the number of parents that correspond to a particular node.
Node degree: A node's degree is determined by how many children it has.
A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.

Binary Tree Representation

Each node in the tree has the following information:

Pointer to the left child
Pointer to the right child

In C, we may use structures to represent a tree node. We may utilise classes as a component of other languages' OOP features. An illustration of a tree node containing integer data is shown below.

// Structure of each node of the tree
struct node {
	int data;
	struct node* left;
	struct node* right;
};

What is Strict Binary Tree?

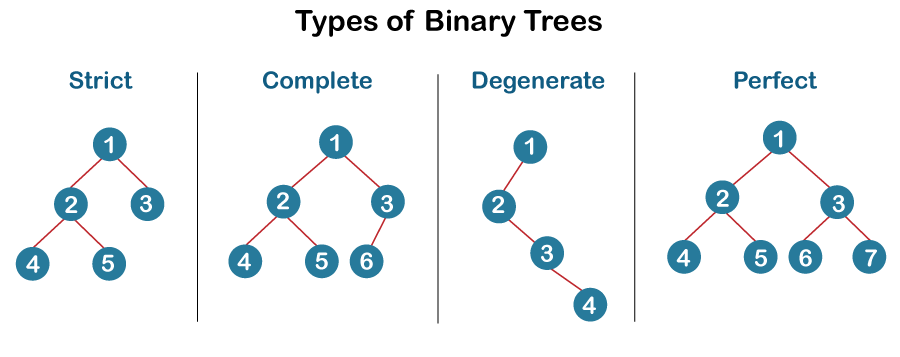
A complete binary tree is another name for the strict binary tree. Only if each node has either 0 or 2 offspring can the tree be regarded as strict binary tree. The term "strict binary tree" can also refer to a tree where all nodes, save the leaf nodes, must have two children.

Let's examine the Full Binary tree as a straightforward example.

The tree shown above is a strict binary tree since each node has either zero or two offspring, as can be seen.

Strict Binary Tree Characteristics

One more than the amount of internal nodes makes up the number of leaf nodes. Given that there are 5 internal nodes in the example above, there are also 6 leaf nodes.
The maximum number of nodes is 2h+1 -1, which corresponds to the number of nodes in the binary tree.
The whole binary tree must have at least 2*h-1 nodes.
The whole binary tree has a minimum height of log2(n+1) - 1.
The entire binary tree's maximum height may be calculated using the formula:
n= 2*h - 1
n+1 = 2*h
h = n+1/2

Complete Binary Tree

Nodes are not added to a new level until the preceding level is fully filled because a Binary tree is known as a Complete Binary tree if all the nodes are added from the left. All of the nodes must be as far to the left as feasible in the final level.

One or two internal nodes may give birth to offspring. However, as the nodes must be inserted starting from the left, only one internal node may have only one child, while the rest will all have 0 or 2 children.
At the bottom level are leaf nodes.
A full binary tree of height h can have up to 2(h+1) - 1 nodes, and it can also have as little as 2 nodes.