How to Check if a Binary Number is Divisible by 3

The problem is to check whether the given binary number is divisible by 3 or a multiple of 3.

This problem is very popular in the programming world and asked in software engineering interviews by none other than Amazon, Microsoft, Adobe, etc.

The binary number can be in the form of a string or an integer. We need to take care of that also before going for the implementation.

Example 1:

binary = "0011"
Output = True

Explanation: The given binary number is 3 in decimal, which is obviously divisible by 3.

Example 2:

binary = "1011"
Output = False

Explanation: The given binary number is 11 in decimal, which is not a multiple of 3.

In this article, we will learn different approaches to solving this problem and discuss the best approach to check if a binary number is a multiple of three.

Method 1 - Converting to Decimal

The simplest approach is to convert the binary number into a decimal equivalent. And check if it is divisible by 3 or not.

To convert the binary number to decimal:

Traverse the number from right to left.
Multiply each digit by 2, raised to the power of its position.
Sum the result on each iteration.

Check if the number is divisible by 3; if yes, the binary number is also divisible by 3.

Below is the Python implementation of the same:

"""
Python program to check if a binary number is
divisible by 3
"""

# Function
def is_divisible_by_three(binary):
    ans = 0
    i = 1

    # Iterating through the binary number digits
    while binary > 0:
        
        # Extracting the rightmost digit and
        # multiplying it by the corresponding power of 2
        ans = ans + i * (binary % 10)
        
        # Removing the rightmost digit
        binary = binary // 10
        
        # Updating the power of 2 for the next digit
        i = i * 2

    # Checking if the sum is divisible by 3
    if ans % 3 == 0:
        return True

    return False

# Binary Numbers
binary1 = 11		# 3 in decimal
binary2 = 1100	# 12 in decimal
binary3 = 1011	# 11 in decimal

# Checking divisibility for binary1
print(f"Is binary1 = {binary1} divisible by 3? {is_divisible_by_three(binary1)}")

# Checking divisibility for binary2
print(f"Is binary2 = {binary2} divisible by 3? {is_divisible_by_three(binary2)}")

# Checking divisibility for binary3
print(f"Is binary3 = {binary3} divisible by 3? {is_divisible_by_three(binary3)}")

Output:

Is binary1 = 11 divisible by 3? True
Is binary2 = 1100 divisible by 3? True
Is binary3 = 1011 divisible by 3? False

Time Complexity = O(n): Where n is the number of digits in the binary number.

Space Complexity - O(1): It uses constant space.

Method 2 - Using DFA (Deterministic Finite Automata) - State Machine Approach

A more efficient approach is to design a DFA that simulates the division process.

The state machine or DFA will have three states: 0, 1, and 2, representing the remainder of the division of the binary number by three.

The diagrammatical representation of the DFA is Given below: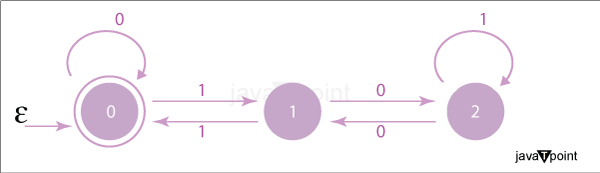

How to Check if a Binary Number is Divisible by 3

We will start from the initial state of 0 and iterate over the binary digits from left to right, updating the state according to the transitions:

If the current state is 0
- If the digit is 0, the state remains 0 - transition: state 0 -> state 0
- If the digit is 1, we move to the next state 1 - transition: state 0 -> state 1
If the current state is 1
- If the digit is 0, we move the state 2 - transition: state 1 -> state 2
- If the digit is 1, we move back to the state 0 - transition: state 1 -> state 0
If the current state is 2
- If the digit is 1, we loop on state 2 - transition: state 2 -> state 2
- if the digit is 0, we move back to the state 1 - transition: state 2 -> state 1

After iterating through all the digits, if the final state is 0, the binary number is divisible by three, and we return True. Otherwise, False.

Below is the Python implementation of the same:

"""
Python program to check if a binary number is
divisible by 3 using DFA
"""

# Function
def is_divisible_by_three(binary):
    state = '0'

    # Iterating through the binary number digits
    for i in binary:
        
        # Using pattern matching to determine the next state
        # based on the current state and the current binary digit
        match state:
            # If the current state is 0
            case '0':
                if i == '1':
                    state = '1'

            # If the current state is 1
            case '1':
                if i == '1':
                    state = '0'
                else:
                    state = '2'

            # If the current state is 2
            case '2':
                if i == '0':
                    state = '1'

    # Checking the final state
    if state == '0':
        return True
    
    return False

# Binary Numbers
binary1 = '11' 	# 3 in decimal
binary2 = '1100' 	# 12 in decimal
binary3 = '1011'	# 11 in decimal

# Checking divisibility for binary1
print(f"Is binary1 = {binary1} divisible by 3? {is_divisible_by_three(binary1)}")

# Checking divisibility for binary2
print(f"Is binary2 = {binary2} divisible by 3? {is_divisible_by_three(binary2)}")

# Checking divisibility for binary3
print(f"Is binary3 = {binary3} divisible by 3? {is_divisible_by_three(binary3)}")

Output:

Is binary1 = 11 divisible by 3? True
Is binary2 = 1100 divisible by 3? True
Is binary3 = 1011 divisible by 3? False

Time Complexity = O(n): Where n is the number of digits in the binary number.

Space Complexity - O(1): It uses constant space for state variables.

But this approach is not the most efficient and also requires prior knowledge of automata.

Method 3 - Bit Manipulation - (|odd bits - even bits|) divisible by 3

This is the most efficient and elegant approach to determining the divisibility of a binary number by three.

We will count the number of ones at odd positions and even positions separately.

If the difference between these counts is divisible by three, then the binary number is divisible by three.

In general, a binary number N can be represented as:

N = b_n 2^n-1+ b_n-1 2^n-2+ b_n-22^n-3+ … + b₂2² + b₁2¹ + b₀2⁰

Where bi represents the binary digit (0 or 1), and n represents the highest power of 2.

Now, let us examine the remainder when each power of 2 is divided by 3:

2^0 % 3 = 1
2^1 % 3 = 2 
2^2 % 3 = 1
2^3 % 3 = 2 
2^4 % 3 = 1
...

We can observe that the remainders alternate between 1 and 2 as the powers of 2 increase.

From the above pattern, the expression (2^k) % 3 can be simplified as follows:

- If k is even, (2^k) % 3 = 1
- If k is odd, (2^k) % 3 = 2

So, for a binary number to be divisible by 3, the difference between the count of ones at an even place and an odd place must be divisible by three.

In a decimal system, if the sum of the digits of a number is divisible by three, then the number is also divisible by 3. Another approach one can follow for ones at even places, we count 2, and ones at odd places, we count 1

If the count is divisible by 3. The binary number would be divisible by 3.

The Python Implementation of Bit Manipulation is given below:

In our approach, we calculate the counts of ones at even and odd positions separately and check if the difference is divisible by 3. If yes, then the binary number is divisible by three. Otherwise, it is not divisible.

"""
Python program to check if a binary number is
divisible by 3 using Bit Manipulation.
"""

# Function
def is_divisible_by_three(binary):

    # Get the length of the binary number
    n = len(binary)

    # Flag to keep track of odd/even positions
    odd_position = True

    # Variables to count the number of ones
    # at even and odd positions
    ones_at_even = 0
    ones_at_odd = 0

    # Iterate through the binary number left-to-right
    for i in range(n-1, -1, -1):

        # If it's an odd position
        if odd_position:
            # Check if the digit is 1 and
            # increment the count of ones at odd positions
            if binary[i] == '1':
                ones_at_odd += 1

            # Set the flag to move to even position
            odd_position = False

            # Skip to the next iteration
            continue

        # If it's an even position
        if not odd_position:
            # Check if the digit is 1 and increment
            # the count of ones at even positions
            if binary[i] == '1':
                ones_at_even += 1

            # Set the flag to move to odd position
            odd_position = True

    # Check if the difference between the counts
    # of ones at even and odd positions is divisible by 3
    return (ones_at_even - ones_at_odd) % 3 == 0

# Binary Numbers
binary1 = '11' # 3 in decimal
binary2 = '1100' # 12 in decimal
binary3 = '1011' # 11 in decimal

# Checking divisibility for binary1
print(f"Is binary1 = {binary1} divisible by 3? {is_divisible_by_three(binary1)}")

# Checking divisibility for binary2
print(f"Is binary2 = {binary2} divisible by 3? {is_divisible_by_three(binary2)}")

# Checking divisibility for binary3
print(f"Is binary3 = {binary3} divisible by 3? {is_divisible_by_three(binary3)}")

Output:

Is binary1 = 11 divisible by 3? True
Is binary2 = 1100 divisible by 3? True
Is binary3 = 1011 divisible by 3? False

Explanation:

In the above example, we iterate over the binary number from right to left (from least significant bit to most significant bit).
The odd_position is initially set to True:
- Once we are at the odd position, we check whether the digit is '1'. If yes, we increment the ones_at_odd by 1.
- And, we set the odd_position to False, indicating that the next index would be even.
If odd_position is set to False means we are at an even index
- We check whether the digit is '1'. If yes, we increment the ones_at_even by 1.
- And, we set the odd_position to True, indicating that the next index would be odd.
Once the loop completes, we calculate the difference between the counts of ones at even and odd positions (ones_at_even - ones_at_odd).
At last, we check if this difference is divisible by 3 ((ones_at_even - ones_at_odd) % 3 == 0).
If the difference is divisible by 3, we return True, indicating that the binary number is divisible by three. Otherwise, we return False.

Time Complexity = O(n), where n is the number of digits in the binary number.

Space Complexity = O(1) as we only need a few variables to store the counters.

Best Approach:

Among the discussed approaches, the Bit Manipulation approach is the most efficient approach to check if a binary number is divisible by three.
This approach is easy to understand, avoids converting to decimal, and directly operates on the binary number.

C++ Implementation:

// C++ program to check if a binary number
// is divisible by 3 using bit manipulation
#include <iostream>
#include <string>
using namespace std;

// Function
bool is_divisible_by_three(string binary) {
    
    // Get the length of the string
    int n = binary.length();
    
    // Falg to keep track of odd/even positions
    bool odd_position = true;
    
    // Variables to count ones at even/odd positions
    int ones_at_even = 0;
    int ones_at_odd = 0;
    
    // Iterate through the binary number left-to-right
    for (int i = n - 1; i >= 0; i--) {
        
        
        // If it's an odd position
        if (odd_position) {
            // Check if the digit is 1 and
            // increment the count of ones at odd positions
            if (binary[i] == '1') {
                ones_at_odd++;
            }
            
            // Set the flag to move to even position
            odd_position = false;
            continue;
        }
        
        // If it's an even position
        if (!odd_position) {
            // Check if the digit is 1 and increment
            // the count of ones at even positions
            if (binary[i] == '1') {
                ones_at_even++;
            }
            
            // Set the flag to move to odd position
            odd_position = true;
        }
    }
    // Check if the difference between the counts
    // of ones at even and odd positions is divisible by 3
    return (ones_at_even - ones_at_odd) % 3 == 0;
}

// Driver function
int main() {
    string binary1 = "11"; // 3 in decimal
    string binary2 = "1100"; // 12 in decimal
    string binary3 = "1011"; // 11 in decimal

    // Checking divisibility for binary1
    cout << "Is binary1 = " << binary1 << " divisible by 3? " << boolalpha << is_divisible_by_three(binary1) << endl;

    // Checking divisibility for binary2
    cout << "Is binary2 = " << binary2 << " divisible by 3? " << boolalpha << is_divisible_by_three(binary2) << endl;

    // Checking divisibility for binary3
    cout << "Is binary3 = " << binary3 << " divisible by 3? " << boolalpha << is_divisible_by_three(binary3) << endl;

    return 0;
}

Output:

C Implementation:

// C program to check if a binary number
// is divisible by 3 using bit manipulation
#include <stdio.h>
#include <stdbool.h>
#include <string.h>

// Function
bool is_divisible_by_three(char* binary) {
    
    // Get the length of the string
    int n = strlen(binary);
    
    // Falg to keep track of odd/even positions
    bool odd_position = true;
    
    // Variables to count ones at even/odd positions
    int ones_at_even = 0;
    int ones_at_odd = 0;
    
    // Iterate through the binary number left-to-right
    for (int i = n - 1; i >= 0; i--) {
        
        // If it's an odd position
        if (odd_position) {
            // Check if the digit is 1 and
            // increment the count of ones at odd positions
            if (binary[i] == '1') {
                ones_at_odd++;
            }
            
            // Set the flag to move to even position
            odd_position = false;
            continue;
        }
        
        // If it's an even position
        if (!odd_position) {
            // Check if the digit is 1 and increment
            // the count of ones at even positions
            if (binary[i] == '1') {
                ones_at_even++;
            }
            
            // Set the flag to move to odd position
            odd_position = true;
        }
    }
    // Check if the difference between the counts
    // of ones at even and odd positions is divisible by 3
    return (ones_at_even - ones_at_odd) % 3 == 0;
}

// Driver Function
int main() {
    char binary1[] = "11"; // 3 in decimal
    char binary2[] = "1100"; // 12 in decimal
    char binary3[] = "1011"; // 11 in decimal

    // Checking divisibility for binary1
    printf("Is binary1 = %s divisible by 3? %s\n", binary1, is_divisible_by_three(binary1) ? "true" : "false");

    // Checking divisibility for binary2
    printf("Is binary2 = %s divisible by 3? %s\n", binary2, is_divisible_by_three(binary2) ? "true" : "false");

    // Checking divisibility for binary3
    printf("Is binary3 = %s divisible by 3? %s\n", binary3, is_divisible_by_three(binary3) ? "true" : "false");

    return 0;
}

Output:

CONCLUSION:

We can use various approaches to check whether a binary number is divisible by three.

We can convert the binary number into its decimal equivalent and then check whether it is divisible by 3 or not.
Another approach is to design a DFA that simulates the division process. The DFA will have three states, 0, 1, and 2 representing the remainder when divided by 3. If we somehow end at state 0. Then we can tell that the binary number is divisible by 3.
The most efficient approach is to determine the difference between the number of ones at odd and even positions. If the difference is divisible by three, the binary number is also divisible by 3.

We can solve the problem in linear time complexity using the last approach. Also, it is the recommended approach for checking binary divisibility by three.

Next TopicStock Buy and Sell Problem

← prev next →