Quick Sort Using Hoare's Partition

In this article, we will discuss how to implement Quick Sort using Hoare's Partition, its applications, and the advantages of Hoare's Partition scheme over the Lomuto partition scheme.

Quick Sort

The idea of this sorting algorithm is to select an element (pivot element) and find its correct position in the array, ensuring that elements left to it must be smaller and elements right to it must be greater. Repeating the same process for the left and right subarrays recursively until the array is sorted.

It is more efficient in terms of memory usage and time and is a widely used search algorithm. It employs the divide and conquer technique to sort an array.

Pseudo Code:

function quickSort(arr, low, high):
	if low < high:
		pivot_index = hoaresPartition(arr, n , low, high)
		quicksort(arr, low, pivot_index-1)
		quicksort(arr, pivot_index+1, high)

Hoare's Partition Scheme:

Sir Charles Antony Richard Hoare developed the Quick Sort algorithm, and both Lomuto and Hoare's partition schemes were proposed by him. Unlike the Lomuto partition, which uses a pivot element and partitions the array based on it, Hoare's partition uses two pointers that traverse the array in opposite directions and makes necessary swaps until the pointer meets.

This partition scheme reduces the number of swaps resulting in a time-efficient performance. Here is how it works:

Pseudo Code:

function hoarePartition(arr, low, high):
    pivot = arr[low]
    i = low - 1 // Initialize left pointer
    j = high + 1 // Initialize right pointer

    while true:
        do:
            i = i + 1
        while arr[i] < pivot // Increment i while arr[i] is less than the pivot

        do
            j = j - 1
        while arr[j] > pivot // Decrement j while arr[j] is greater than the pivot

        if i >= j: // If i and j meet or cross each other
            return j // Return partition index

        swap(arr[i], arr[j])

The elements left to the partition index will be smaller than or equal to the pivot. And elements right to the partition index will be greater or equal to the partition.

Time Complexity Analysis:

Average Case Analysis:

Time Complexity: T(N) = O(N logN)
Recurrence Relation: T(N) = T(N/10) + T(9N/10) + O(N)

In the average case, we consider that the partition is not fairly dividing the array into two halves. We consider 1/10 elements in the first half and 9/10 in the second half.

Worst Case Analysis:

Time Complexity: T(N) = O(N2)
Recurrence Relation: T(N) = T(N-1) + O(N)

It performs worse when we pass an array sorted in ascending or descending order. In the worst case, the partition function selects the smallest or the largest element each time, resulting in poor performance.

Space Complexity Analysis:

The quick sort algorithm is an in-place sorting algorithm and does not require extra space to store elements. It requires auxiliary space for the recursion call stack.

In the worst case, the recursion call stack requires Θ(n) space.

Below is the snapshot of the recursion call stack: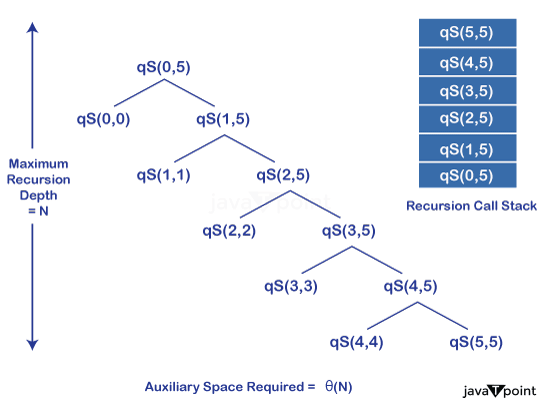

Python Implementation:

# Quick Sort Function
def quickSort(arr, low, high):
    # Base case: if the sub-array has more than one element
    if low < high:
        # Partition the array using Hoare's Partition scheme
        i = hoarePartition(arr, low, high)
        
        # Recursively sort the left sub-array
        quickSort(arr, low, i)
        
        # Recursively sort the right sub-array
        quickSort(arr, i + 1, high)

# Hoare's Partition Function
def hoarePartition(arr, low, high):
    # Choose the first element as the pivot
    pivot = arr[low]
    
    # Initialize pointers:
    left = low - 1 # Left Pointer
    right = high + 1 # Right Pointer

    # Start an infinite loop to traverse the array and rearrange elements
    while True:
        # Move the left pointer to the right until
        # an element greater than or equal to the pivot is found
        left += 1
        while arr[left] < pivot:
            left += 1
        
        # Move the right pointer to the left until
        # an element less than or equal to the pivot is found
        right -= 1
        while arr[right] > pivot:
            right -= 1
        
        # If the left pointer crosses or becomes equal
        # to the right pointer, the partitioning is complete
        if left >= right:
            # Return the right pointer position
            # as the index for the next partition
            return right
        
        # Swap the elements at the left and right pointers
        arr[left], arr[right] = arr[right], arr[left]

# Sample array
arr = [10, 2, 16, 22, 35, 17, 26, 3, 9, 13]
print(f"Unsorted Array: {arr}")

# Call quickSort to sort the array
quickSort(arr, 0, 9)
print(f"Sorted Array: {arr}")

Output:

Explanation:

We have a list: arr = [10, 2, 16, 22, 35, 17, 26, 3, 9, 13], n = 10.

Calling: quickSort(arr, 0, 9)

Here, low = 0 and high = 9, and the low is less than the high:

The quickSort() function calls the hoarePartition(arr, 0, 9). When it returns the partition index, quickSort() calls itself with the following parameters: quickSort(arr, low, i) and quickSort(arr, i+1, high).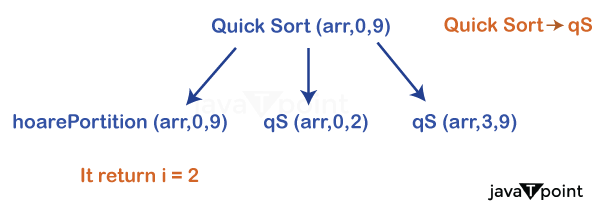

The whole idea resides in the partitioning scheme. So, it is important to understand Hoare's Partition Scheme. You can find the brief explanation of quick sort using Lomuto Partition here.

Lets us now understand the working of the hoarePartition() function.

def hoarePartition(arr, low, high):
    pivot = arr[low]
    left = low - 1 # Left Pointer
    right = high + 1 # Right Pointer

It selects the first element of the subarray as a pivot to compare other elements. Here, pivot = arr[0] = 10, Initializes the left and right pointer as follows:

left = -1

right = 10

It then starts an infinite loop to traverse the array.

left += 1
left = -1 + 1 = 0

It initializes the left = 0 pointer and moves it towards the right until it finds an element greater than or equal to the pivot.

while arr[left] < pivot:
    left += 1

left = 0

arr[left] = 10 equal to the pivot = 10: It breaks the loop at left = 0 as the while condition is unsatisfied.

right -= 1
right = 10 - 1 = 9

It then initializes the right = 9 and moves it toward the left until it finds an element less than or equal to the pivot.

while arr[right] > pivot:
    right -= 1

right = 8

arr[right] = 9 less than the pivot = 10: It breaks the loop at right = 8 as the while condition is unsatisfied.

if left >= right:
    return right

We then check if the left crosses the right or not. Here, the if-condition is unsatisfied.

We then swap the elements at left = 0 and right = 8.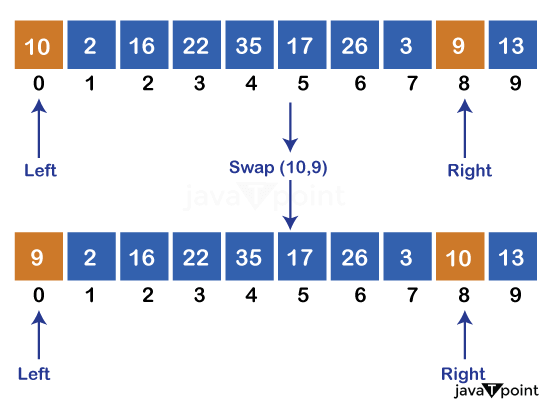

It starts the next iteration as the left pointer is less than the right pointer.

In the second iteration:

It swaps the element at left = 2 and right = 7: swap(arr[left] = 16, arr[right] = 3)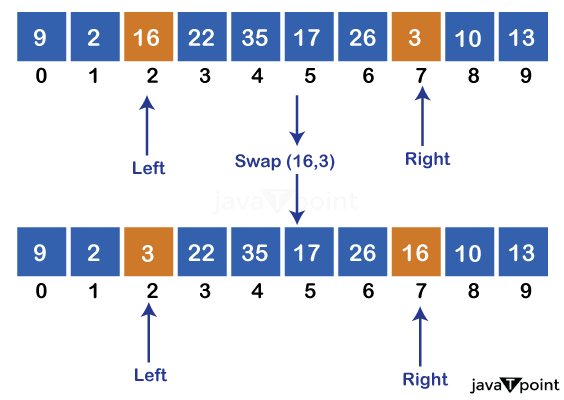

In the third iteration:

The left pointer stops at index 3, arr[left] = 22, and the right pointer stops at 2, arr[right] = 3.

if left >= right:
    return right

In this iteration, the left pointer becomes greater than the right, and hoarePartition() returns right = 2.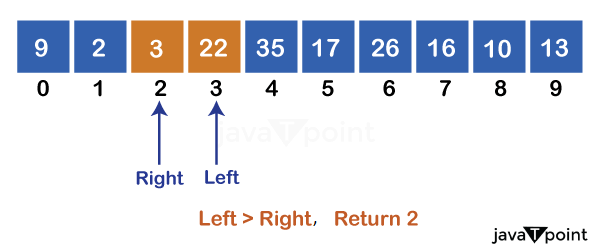

Let us have a quick overview of a few more function calls.

Calling: quicksort(arr, 0, 2)

In this call, the hoarePartition() swaps (9, 3) and returns 1, and function calls are made accordingly.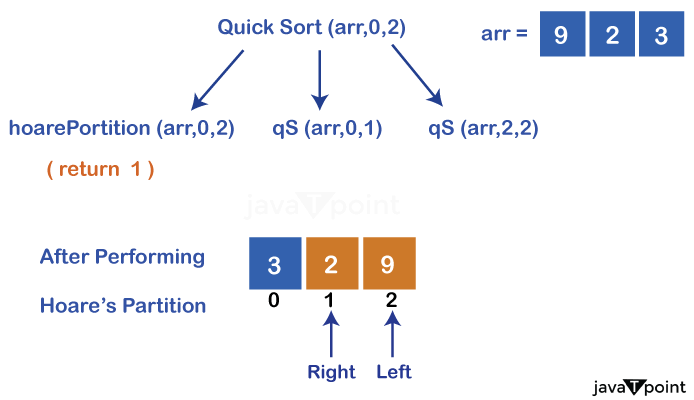

The above recursion tree shows how to proceed with the next function calls.

Calling: quicksort(arr, 3, 9)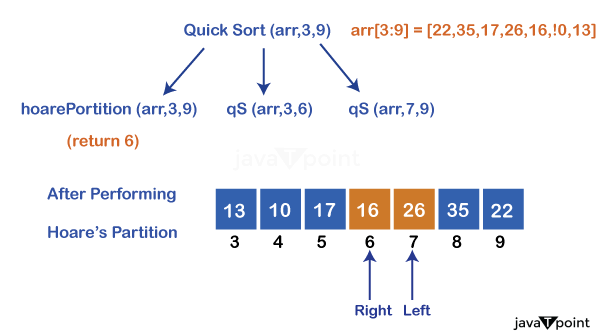

In this call, the hoarePartition() first swaps (22, 13), then swaps(35, 10), lastly swaps(26, 16) and returns 6.

This process is recursively repeated for all possible recursion calls, and ultimately the array gets sorted.

C++ Implementation:

#include <iostream>
using namespace std;

// Function to swap two elements in the array
void swap(int arr[], int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// Function to print the elements of the array
void printArray(int arr[], int n){
    for (int i = 0; i < n; i++){
        cout << arr[i] << " ";
    }
    cout << endl;
}

// Function implementing Hoare's Partition for Quick Sort
int hoarePartition(int arr[], int low, int high){
    // Choose the first element as pivot element
    int pivot = arr[low];
    
    // Initialize two pointers:
    int left = low - 1; // Left Pointer
    int right = high + 1; // Right Pointer

    // Start an infinite loop to traverse the array
    while (1) {
        // Move left pointer to the right until
        // an element greater than or equal to the pivot is found
        left++;
        while (arr[left] < pivot){
            left++;
        }
        
        // Move right pointer to the left until
        // an element less than or equal to the pivot is found
        right--;
        while (arr[right] > pivot){
            right--;
        }
        
        // If the left pointer crosses or becomes equal to the right pointer,
        // the partitioning is complete
        if (left >= right){
            // Return the right pointer position as the index
            // for the next partition
            return right;
        }
        
        // Swap the elements at the left and right pointers
        swap(arr, left , right);
    }
}

// Function implementing Quick Sort using Hoare's Partition
void quickSort(int arr[], int low, int high){
    // Base case: if the sub-array has more than one element
    if (low < high){
        // Partition the array using Hoare's Partition
        // and get the index of the pivot
        int i = hoarePartition(arr, low, high);
        
        // Recursively sort the left sub-array
        // (elements before the pivot)
        quickSort(arr, low, i);
        
        // Recursively sort the right sub-array
        // (elements after the pivot)
        quickSort(arr, i+1, high);
    }
}

int main() {
    // Write C++ code here
    int arr[] = {14, 8, 22, 16, 12, 5, 6, 25, 2, 9};
    int n = 10;
    
    // Print array
    cout << "Unsorted Array: ";
    printArray(arr, 10);
    
    // Call quickSort to sort the array
    quickSort(arr, 0, 9);
    
    // Print array
    cout << "Sorted Array: ";
    printArray(arr, 10);

    return 0;
}

Output:

C Implementation:

 #include <stdio.h>

// Function to swap two elements in the array
void swap(int arr[], int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// Function to print the elements of the array
void printArray(int arr[], int n){
    for (int i = 0; i < n; i++){
        printf("%d ",arr[i]);
    }
    printf("\n");
}

// Function implementing Hoare's Partition for Quick Sort
int hoarePartition(int arr[], int low, int high){
    // Choose the first element as pivot element
    int pivot = arr[low];
    
    // Initialize two pointers:
    int left = low - 1; // Left Pointer
    int right = high + 1; // Right Pointer

    // Start an infinite loop to traverse the array
    while (1) {
        // Move left pointer to the right until
        // an element greater than or equal to the pivot is found
        left++;
        while (arr[left] < pivot){
            left++;
        }
        
        // Move right pointer to the left until
        // an element less than or equal to the pivot is found
        right--;
        while (arr[right] > pivot){
            right--;
        }
        
        // If the left pointer crosses or becomes equal to the right pointer,
        // the partitioning is complete
        if (left >= right){
            // Return the right pointer position as the index
            // for the next partition
            return right;
        }
        
        // Swap the elements at the left and right pointers
        swap(arr, left , right);
    }
}

// Function implementing Quick Sort using Hoare's Partition
void quickSort(int arr[], int low, int high){
    // Base case: if the sub-array has more than one element
    if (low < high){
        // Partition the array using Hoare's Partition
        // and get the index of the pivot
        int i = hoarePartition(arr, low, high);
        
        // Recursively sort the left sub-array
        // (elements before the pivot)
        quickSort(arr, low, i);
        
        // Recursively sort the right sub-array
        // (elements after the pivot)
        quickSort(arr, i+1, high);
    }
}

int main() {
    // Write C++ code here
    int arr[] = {6, 8, 2, 16, 22, 3, 9, 33, 6, 17};
    int n = 10;
    
    // Print array
    printf("Unsorted Array: ");
    printArray(arr, 10);
    
    // Call quickSort to sort the array
    quickSort(arr, 0, 9);
    
    // Print array
    printf("Sorted Array: ");
    printArray(arr, 10);

    return 0;
}

Output:

Advantages of Hoare's Partition over Lomuto Partition:

Hoare's Partition offers several advantages over Lomuto Partition, making it a preferred choice in certain scenarios:

Fewer swaps: It reduces the number of swaps required during partitioning. Swapping elements is a computationally expensive operation, and reducing the number of swaps enhances the overall performance of the algorithm.
Improved efficiency: Due to fewer swaps, it typically exhibits better performance than Lomuto Partition. It takes much faster than the Lomuto, making it a more efficient partitioning scheme.
Better handling of duplicate elements: Lomuto Partition does not handle duplicate elements efficiently. In contrast, it handles duplicates more effectively, resulting in a more balanced partitioning and improved overall performance.

However, like Lomuto Partitioning, it also does not guarantee stability. The order of identical elements may change.

Conclusion:

Quick sort is an in-place sorting algorithm and follows the divide-and-conquer technique. It utilizes Hoare's Partition, which offers excellent and time-efficient partitioning. It improves the performance of the quick sort algorithm, resulting in faster sorting times compared to Lomuto Partition. Quick Sort is a popular choice for efficiently sorting large datasets. When stability is not that important, it is preferred over merge sort. It is cache friendly, as it operates on all the data, and all data can be stored in the cache.

Next TopicLongest common substring

← prev next →