Types of Sparse Matrices?

In this article, we will understand the sparse matrices and their types in detail.

What do you mean by Sparse Matrices?

A wide range of numerical problems in real-life applications such as engineering, scientific, computing, and economic use huge matrices. These matrices often contain many zero elements, and such matrices with high proportions of zero entries are known as sparse matrices.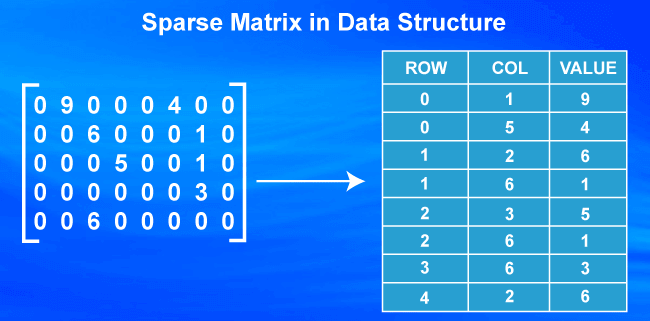

It is called sparse as it has a relatively low density of non-zero elements. If we store Sparse Matrix as a 2-dimension array, a lot of space is wasted to store all those 0's explicit. Moreover, while performing operations on sparse matrices such as addition, subtraction, and multiplication stored as a 2-dimension array, many operations are performed on elements with zero values which results in the amount of wastage in time. So, a better strategy is to explicitly store the non-zero elements, which greatly reduces the required storage space and computations needed to perform various operations.

Types of Sparse Matrices

There are different variations of sparse matrices, which depend on the nature of the sparsity of the matrices. Based on these properties, sparse matrices can be

• Regular sparse matrices
• Irregular sparse matrices / Non - regular sparse matrices

Regular sparse matrices

A regular sparse matrix is a square matrix with a well-defined sparsity pattern, i.e., non-zero elements occur in a well-defined pattern. The various types of regular sparse matrices are:

• Lower triangular regular sparse matrices
• Upper triangular regular sparse matrices
• Tri-diagonal regular sparse matrices

Lower triangular regular sparse matrices

A Lower regular sparse matrix is the one where all elements above the main diagonal are zero value. The following matrix is a lower triangular regular sparse matrix.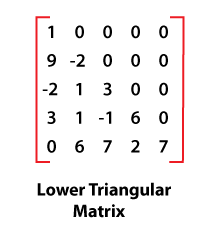

Storing Lower triangular regular sparse matrices

In a lower triangular regular sparse matrix, the non-zero elements are stored in a 1-dimensional array row by row.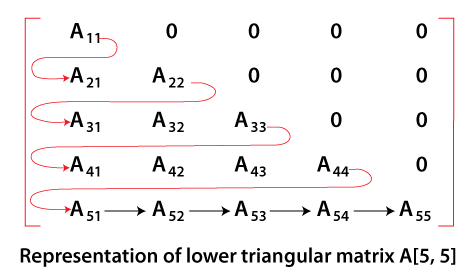

For example: The 5 by 5 lower triangular regular sparse matrix as shown in the above figure is stored in one-dimensional array B is:

B = { A₁₁, A₂₁, A₂₂, A₃₁, A₃₂, A₃₃, A₄₁, A₄₂, A₄₃, A₄₄, A₅₁, A₅₂, A₅₃, A₅₄, A₅₅}

Here B [1] = A₁₁, B [2] = A₂₁, B [3] = A₂₂, ……………………………………… B [14] = A_54, B [15] = A₅₅

To calculate the total number of non-zero elements, we need to know the number of non-zero elements in each row and then add them. Since the number of non-zero elements in an ith row so that the total number of non-zero elements in the lower triangular regular sparse matrix of n rows is:

1 + 2 + ………………… + i + ………………….. + (n-1) + n = n (n+1)/2

Upper triangular regular sparse matrices

The Upper triangular regular sparse matrix is where all the elements below the main diagonal are zero value. Following matrix is the Upper triangular regular sparse matrix.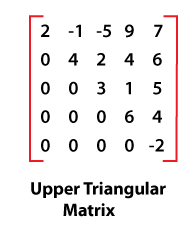

Storing Upper triangular regular sparse matrices

In an upper triangular regular sparse matrix, the non-zero elements are stored in a 1-dimensional array column by column.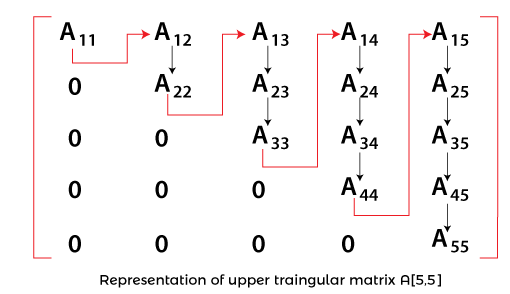

For example, The 5 by 5 lower triangular regular sparse matrix, as shown in the above figure, is stored in one-dimensional array B is:

B = { A₁₁, A₂₁, A₂₂, A₃₁, A₃₂, A₃₃, A₄₁, A₄₂, A₄₃, A₄₄, A₅₁, A₅₂, A₅₃, A₅₄, A₅₅}

Here B [1] = A₁₁, B [2] = A₂₁, B [3] = A₂₂, B [4] = A_31,B [5] = A_{32 ,}B [6] = A_33, B [7] = A_{41 ,}B [8] = A_{42 ,}B [9] = A_{43 ,}B [10] = A_{44 ,}B [11] = A_{51 ,}B [12] = A_{52 ,}B [13] = A₅₃ , B [14] = A_54, B [15] = A₅₅

In order to calculate the total number of non-zero elements, we need to know the number of non-zero elements in each row and then add them. Since, the number of non-zero elements in ith row so that the total number of non-zero elements in lower triangular regular sparse matrix of n rows is:

1 + 2 + ………………… + i + ………………….. + (n-1) + n = n (n+1)/2

Upper triangular regular sparse matrices

The Upper triangular regular sparse matrix is where all the elements below the main diagonal are zero value. The following matrix is an Upper triangular regular sparse matrix.

Storing Upper triangular regular sparse matrices

In an upper triangular regular sparse matrix, the non-zero elements are stored in a 1-dimensional array column by column.

For example, The 5 by 5 lower triangular regular sparse matrix, as shown in the above figure, is stored in one-dimensional array B is:

C = { A₁₁, A₁₂, A₂₂, A₁₃, A₂₃, A₃₃, A₁₄, A₂₄, A₃₄, A₄₄, A₁₅, A₂₅, A₃₅, A₄₅, A₅₅}

Here C [1] = A₁₁, C [2] = A₁₂, C [3] = A₂₂, C [4] = A_13,C [5] = A_{23 ,}C [6] = A_33, C [7] = A_{14 ,}C [8] = A_{24 ,}C [9] = A₃₄, C [10] = A_{44 ,}C [11] = A_{15 ,}C [12] = A_{25 ,}C [13] = A₃₅ , C [14] = A_45, C [15] = A₅₅

In order to calculate the total number of non-zero elements, we need to know the number of non-zero elements in each column and then add them. Since, the number of non-zero elements in ith column is i so the total number of non-zero elements in upper triangular regular sparse matrix of n columns is:

1 + 2 + ………………… + i + ………………….. + (n-1) + n = n (n+1)/2

Tri-diagonal regular sparse matrices

The tridiagonal regular sparse matrix where all non-zero elements lie on one of the three diagonals, the main diagonal above and below.

Storing Tri-diagonal regular sparse matrices

In a tri-diagonal regular sparse matrix, all the non-zero elements are stored in a 1-dimensional array row by row.

For example, The 5 by 5 tri-diagonal regular sparse matrix, as shown in the above figure, is stored in one-dimensional array D is:

D = { A₁₁, A₁₂, A₂₁, A₂₂, A₂₃, A₃₂, A₃₃, A₃₄, A₄₃, A₄₄, A₄₅, A₅₄, A₅₅}

Here D [1] = A₁₁, D [2] = A₁₂, D [3] = A₂₁, D [4] = A_22, D [5] = A_23, D [6] = A_{32 ,}D [7] = A_33, D [8] = A_{34 ,}D [9] = A_{43 ,}D [10] = A_{44 ,}D [11] = A_{45 ,}D [12] = A_54, D [13] = A₅₅

In order to calculate the total number of non-zero elements, we need to know the number of non-zero elements along the diagonal, above the diagonal and below the diagonal. The number of elements in a square matrix along the diagonal is 'n' and above the diagonal is (n-1). So the total number of non-zero elements in n-square matrix is:

Therefore, the total number of elements for n-squre matrix = 3n-2

In our case, n = 5 so the total number of elements = 3 * 5 - 2 = 13

Irregular sparse matrices

The irregular sparse matrices are the ones that behave an irregular or unstructured pattern of occurrences of non-zero elements. The following matrix is an irregular sparse matrix.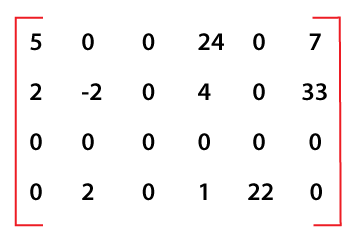

In the above diagram, there are several common storage schemes to store sparse matrices. Most of these schemes store all the non-zero elements of the matrix into a 1-dimensional array.

Storage schemes of Irregular sparse matrices:

In this scheme, we store all the non-zero elements of the matrix into a 1-dimensional array and use several auxiliary arrays to specify the location of non-zero elements in the sparse matrix. Among the several available storage schemes for storing irregular sparse matrices, the most common storage schemes are:

• Storage by Index Method
• Storage by Compressed Row Format

Storing irregular sparse matrix using storage by Index Method

Using storage by the index method, we can store irregular sparse matrices A by constructing three 1-Dimensional arrays AN, AI, and AJ, each having elements equal to a total number of non-zero elements.

• The array AN contains the non-zero elements stored row contiguously by row.
• AI contains the corresponding row number of non-zero elements A[I, J] in matrix A.
• AJ contains the corresponding column number of non-zero elements A[I, J] in matrix A.

Let us consider a 4 by 6 sparse matrix A as shown below:

Out of 24 elements of this Sparse Matrix, only 10 elements are non-zero. These non-zero elements are: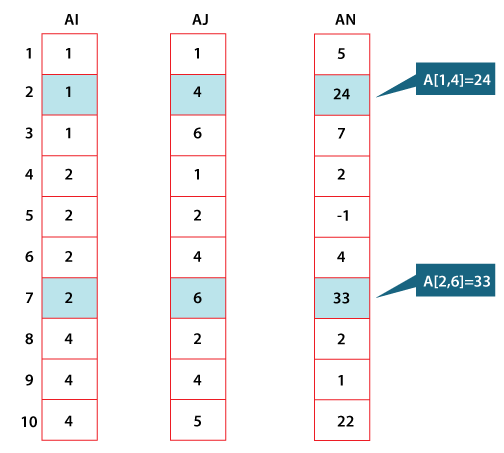

Figure: Representation of three 1 - D arrays AI, AJ, AN

To store it using the storage by index method. We construct three-dimensional arrays AN, SI, AJ, each having 10 elements (i.e., the total number of non-zero elements) as shown in the above diagram.

The array AN contains the 10 non-zero elements stored contiguously. The corresponding row number and column number of each non-zero element are stored in arrays AI and AJ, respectively.

Storing irregular sparse matrix using the compressed row storage format

Another space-efficient and most widely used scheme for representing irregular sparse matrices is compressing row storage. In this scheme, we take three 1-Dimensional arrays AN, AI, and AJ. One-dimensional array AN contains all the values of non-zero elements taken in a row-wise fashion from the matrix. The next 1-dimensional array AJ of length equal to AN's length is constructed that contains the original column positions of the corresponding elements in AN. A 1-dimensional array AI with a length equal to several rows is constructed that stores the location of the first entry of non-zero elements in AN array.

For Example:

AI [2] = 4 indicates that the first non-zero elements in row 2 are stored in AN[4], which is 2.

To store it by compressing row storage format, we construct three 1-dimensional arrays AN, AI, and AJ, as shown in the following figure: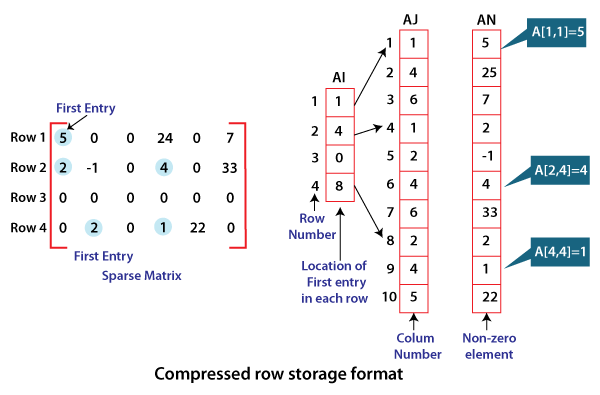

The array AN contains 10 non-zero elements stored contiguously in a row-wise fashion. The corresponding column numbers are stored in 1-dimensional array AJ. The 1-dimensional array AI contains elements which is pointer to the first non-zero element of each row in array AJ and AN.