Sparse Matrix

In this article, we will discuss the sparse matrix.

Let's first see a brief description of the matrix.

What is a matrix?

A matrix can be defined as a two-dimensional array having 'm' rows and 'n' columns. A matrix with m rows and n columns is called m � n matrix. It is a set of numbers that are arranged in the horizontal or vertical lines of entries.

For example -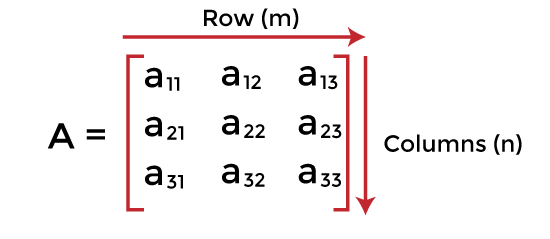

What is a sparse matrix?

Sparse matrices are those matrices that have the majority of their elements equal to zero. In other words, the sparse matrix can be defined as the matrix that has a greater number of zero elements than the non-zero elements.

Now, the question arises: we can also use the simple matrix to store the elements, then why is the sparse matrix required?

Why is a sparse matrix required if we can use the simple matrix to store elements?

There are the following benefits of using the sparse matrix -

Storage - We know that a sparse matrix contains lesser non-zero elements than zero, so less memory can be used to store elements. It evaluates only the non-zero elements.

Computing time: In the case of searching in sparse matrix, we need to traverse only the non-zero elements rather than traversing all the sparse matrix elements. It saves computing time by logically designing a data structure traversing non-zero elements.

Representation of sparse matrix

Now, let's see the representation of the sparse matrix. The non-zero elements in the sparse matrix can be stored using triplets that are rows, columns, and values. There are two ways to represent the sparse matrix that are listed as follows -

Array representation
Linked list representation

Array representation of the sparse matrix

Representing a sparse matrix by a 2D array leads to the wastage of lots of memory. This is because zeroes in the matrix are of no use, so storing zeroes with non-zero elements is wastage of memory. To avoid such wastage, we can store only non-zero elements. If we store only non-zero elements, it reduces the traversal time and the storage space.

In 2D array representation of sparse matrix, there are three fields used that are named as -

Row - It is the index of a row where a non-zero element is located in the matrix.
Column - It is the index of the column where a non-zero element is located in the matrix.
Value - It is the value of the non-zero element that is located at the index (row, column).

Example -

Let's understand the array representation of sparse matrix with the help of the example given below -

Consider the sparse matrix -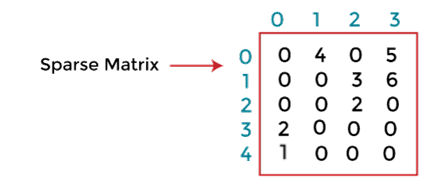

In the above figure, we can observe a 5x4 sparse matrix containing 7 non-zero elements and 13 zero elements. The above matrix occupies 5x4 = 20 memory space. Increasing the size of matrix will increase the wastage space.

The tabular representation of the above matrix is given below -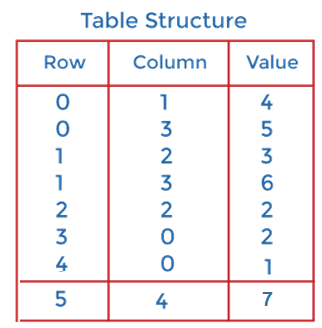

In the above structure, first column represents the rows, the second column represents the columns, and the third column represents the non-zero value. The first row of the table represents the triplets. The first triplet represents that the value 4 is stored at 0th row and 1st column. Similarly, the second triplet represents that the value 5 is stored at the 0th row and 3rd column. In a similar manner, all triplets represent the stored location of the non-zero elements in the matrix.

The size of the table depends upon the total number of non-zero elements in the given sparse matrix. Above table occupies 8x3 = 24 memory space which is more than the space occupied by the sparse matrix. So, what's the benefit of using the sparse matrix? Consider the case if the matrix is 8*8 and there are only 8 non-zero elements in the matrix, then the space occupied by the sparse matrix would be 8*8 = 64, whereas the space occupied by the table represented using triplets would be 8*3 = 24.

Implementation of array representation of the sparse matrix

Now, let's see the implementation of array representation of sparse matrix in C language.

In the program below, we will show the tabular representation of the non-zero elements of the sparse matrix stored in array.

#include <stdio.h>
int main()
{
    // Sparse matrix having size 4*5
    int sparse_matrix[4][5] =
    {
        {0 , 0 , 6 , 0 , 9 },
        {0 , 0 , 4 , 6 , 0 },
        {0 , 0 , 0 , 0 , 0 },
        {0 , 1 , 2 , 0 , 0 }
    };
   // size of matrix
    int size = 0;
    for(int i=0; i<4; i++)
    {
        for(int j=0; j<5; j++)
        {
            if(sparse_matrix[i][j]!=0)
            {
                size++;
            }
        }
    }
   // Defining final matrix
    int matrix[3][size]; 
     int k=0;
   // Computing final matrix
    for(int i=0; i<4; i++)
    {
        for(int j=0; j<5; j++)
        {
            if(sparse_matrix[i][j]!=0)
            {
                matrix[0][k] = i;
                matrix[1][k] = j;
                matrix[2][k] = sparse_matrix[i][j];
                k++;
            }
      }
    }
   // Displaying the final matrix
    for(int i=0 ;i<3; i++)
    {
        for(int j=0; j<size; j++)
        {
            printf("%d ", matrix[i][j]);
            printf("\t");
        }
        printf("\n");
    }
    return 0;
}

Output

In the output, first row of the table represent the row location of the value, second row represents the column location of the value, and the third represents the value itself.

In the below screenshot, the first column with values 0, 2, and 6 represents the value 6 stored at the 0^th row and 2^nd column.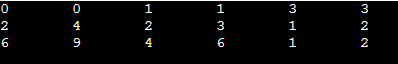

Linked List representation of the sparse matrix

In a linked list representation, the linked list data structure is used to represent the sparse matrix. The advantage of using a linked list to represent the sparse matrix is that the complexity of inserting or deleting a node in a linked list is lesser than the array.

Unlike the array representation, a node in the linked list representation consists of four fields. The four fields of the linked list are given as follows -

Row - It represents the index of the row where the non-zero element is located.
Column - It represents the index of the column where the non-zero element is located.
Value - It is the value of the non-zero element that is located at the index (row, column).
Next node - It stores the address of the next node.

The node structure of the linked list representation of the sparse matrix is shown in the below image -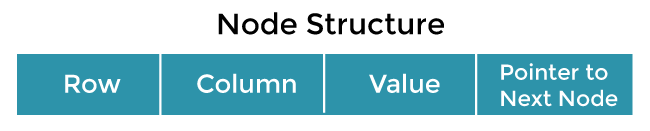

Example -

Let's understand the linked list representation of sparse matrix with the help of the example given below -

Consider the sparse matrix -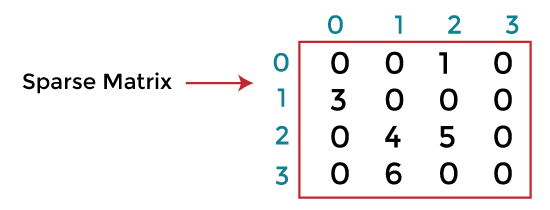

In the above figure, we can observe a 4x4 sparse matrix containing 5 non-zero elements and 11 zero elements. Above matrix occupies 4x4 = 16 memory space. Increasing the size of matrix will increase the wastage space.

The linked list representation of the above matrix is given below -

In the above figure, the sparse matrix is represented in the linked list form. In the node, the first field represents the index of the row, the second field represents the index of the column, the third field represents the value, and the fourth field contains the address of the next node.

In the above figure, the first field of the first node of the linked list contains 0, which means 0^th row, the second field contains 2, which means 2^nd column, and the third field contains 1 that is the non-zero element. So, the first node represents that element 1 is stored at the 0^th row-2^nd column in the given sparse matrix. In a similar manner, all of the nodes represent the non-zero elements of the sparse matrix.

Implementation of linked list representation of sparse matrix

Now, let's see the implementation of linked list representation of sparse matrix in Java.

class Node {
int row;
int col;
int value;
Node next;
Node(int r, int c, int val) 
{ row = r; col = c; this.value = val; }
}
public class Sparse{
public static void main(String[] args)
{
/*Assume a 4x4 sparse matrix */
int sparseMatrix[][] = {
{0, 0, 1, 2},
{3, 0, 0, 0},
{0, 4, 5, 0},
{0, 6, 0, 0}
};
Node start = null; /*Start with the empty list*/
Node tail = null;
int k = 0;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
{
if (sparseMatrix[i][j] != 0) /*Pass only non-zero values*/
{
Node temp = new Node(i, j, sparseMatrix[i][j]);
temp.next = null;
if(start == null){
start = temp;
tail=temp;
}
else{
tail.next = temp;
tail = tail.next;
}
}
}
Node itr = start;
while(start != null){
System.out.println(start.row  + " " + start.col + " " + start.value);
start = start.next;
}
}
}

Output

Every row in the output represents the node of the linked list. In every row of the below screenshot, the first element represents the row index location of the non-zero element, the second element represents the column index location of the non-zero element, and the third element represents the non-zero element itself.

So, that's all about the article. In this article, we have first discussed the brief description of Matrix and Sparse Matrix. After that, we saw why the sparse matrix is useful, and at last, we have discussed the array and linked list representation of the sparse matrix. Hope, the article will be helpful and informative to you.

Next TopicDetect loop in a Linked list

← prev next →