Reversing a Queue

Reversing a queue is the process of making the first element as last and the last element as first. By reversing a queue, we alter the sequence in which its elements will be processed or accessed. This can be done by storing the temporary components in the Stack and then returning them to the Queue whenever required in reverse order.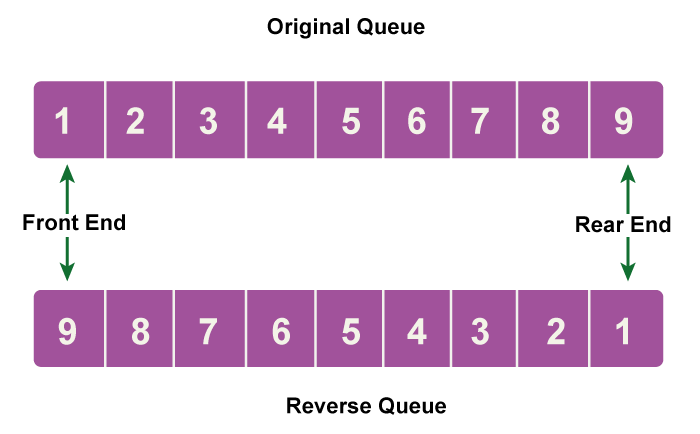

The above picture shows the clear difference between the original (given) queue and the reversed queue. The front and rear ends are used to reverse the queue.

Steps to reverse a Queue

Step 1: Create a Queue and a Stack initially.

Both Arrays or linked lists can be used to implement. Assume we're working with an array-based implementation.

Step 2: Enqueue Elements into the Queue

Add some components to the Queue to populate it.

Step 3: Move Elements from the Queue to the Stack is the third phase. Begin by moving all of the elements from the Queue to the Stack. Repeat through the Queue's items, inserting each one with the Stack's push function.

Step 4: Transfer Elements from the Stack to Queue

Next, transfer the elements from the Stack back to the Queue in the reversed order. Iterate over the elements in the Stack and use the Queue's enqueue operation to insert each element. This step effectively reverses the elements in the Queue.

Step 5: Reversed Queue

At this point, the original Queue has been reversed. You can now perform operations in the reversed Queue as desired.

Algorithm Overview

The process of reversing a queue using a stack as an auxiliary data structure can be summarized as follows:

Initialize a queue and a stack.
Enqueue elements into the Queue.
Transfer elements from the Queue to the Stack.
Transfer elements from the Stack back to the Queue in the reversed order.
The resulting Queue is the reversed version of the original Queue.
Perform operations in the reversed Queue if needed.

You can successfully reverse a queue using a stack as an auxiliary data structure if you follow these instructions. Remember to customize the implementation to your programming language.

Example Implementation

Here's a Python implementation of the above algorithm:

Below shown is the reverse function using Stack in Python.

def reverseQueue(queue): 
    stack = [] 
     
    while not queue.empty(): 
        element = queue.dequeue() 
        stack.append(element) 
     
    while stack: 
        element = stack.pop() 
        queue.enqueue(element) 
     
    return queue 

In this implementation, Queue represents the input queue that you want to reverse. The reverseQueue function uses the empty, dequeue, append, and pop methods to manipulate the Queue and Stack.

Using a stack as an auxiliary data structure, you may reverse a queue. The technique includes moving all elements from the Queue to the Stack and then returning them to the Queue in reverse order. Below is a way to reverse a queue process by stage:

Example:

Let's take an example of how to reverse a queue using the auxiliary stack approach. Consider the following Queue:

Original Queue: [15, 2, 19, 3]

1. As per the first step, we initialize an empty queue and an empty stack.

Queue: [] Stack: []

2. As per the second step, enqueue elements into the Queue

We enqueue the elements [15, 2, 19, 3] into the Queue.

Queue: [15, 2, 19, 3] Stack: []

3. As per the third step, move all the elements from Queue to Stack

Queue: [] Stack: [15, 2, 19, 3]

4. Transfer Elements from Stack to Queue

Queue: [3, 19, 2, 15] Stack: []

5. Reversed Queue

The original Queue has been successfully reversed.

The resulting Queue is [3, 19, 2, 15]

We can perform any operations we want on the reversed Queue at this point.

This is an example of how to reverse a queue using an auxiliary stack.

Here's an example implementation of the queue reversal algorithm in Python:

Below is an example for the Python code, which reverses the given original queue as shown in the first image.

Execution and Output: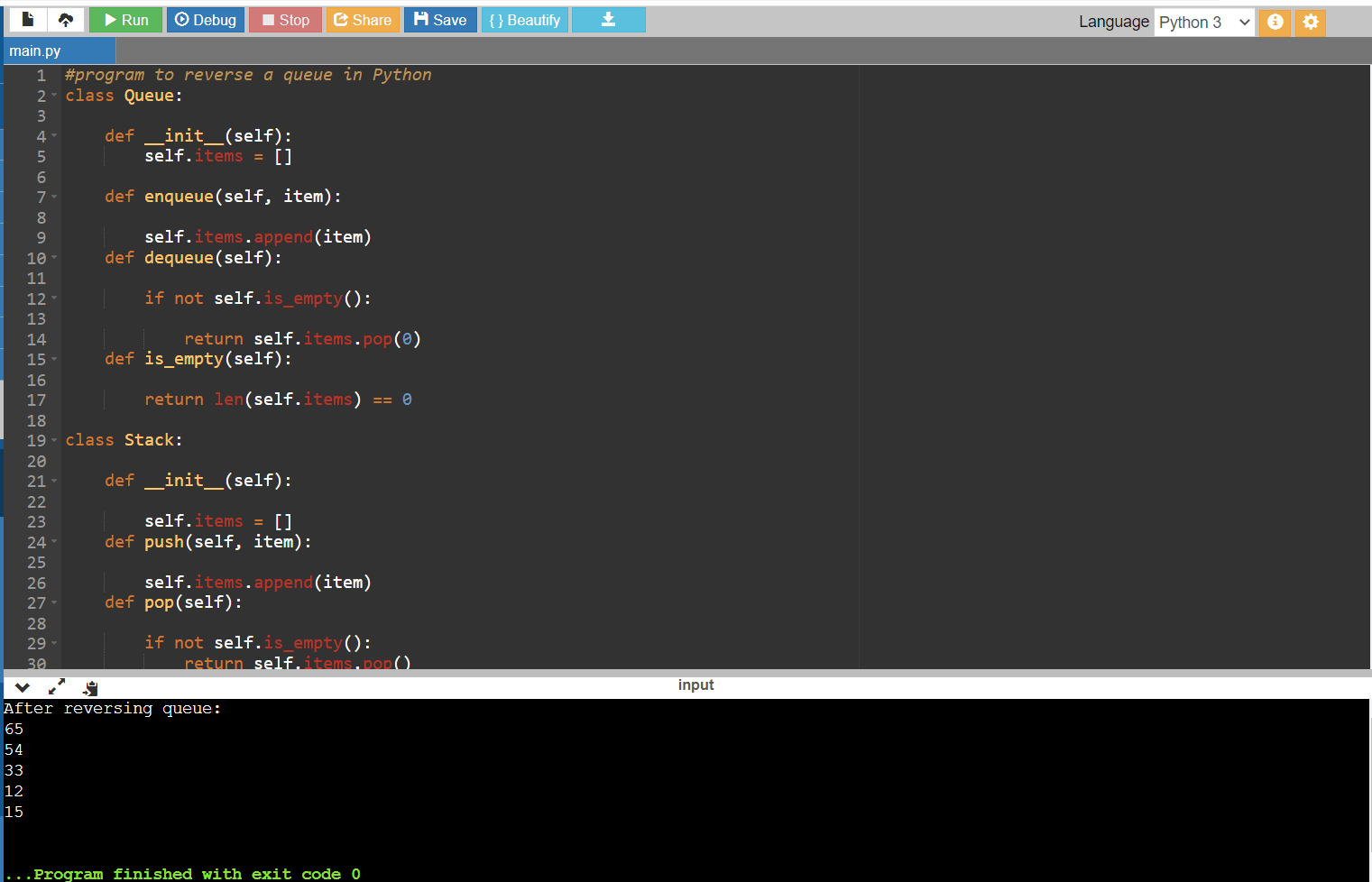

#program to reverse a queue in Python
 
class Queue:  
    def __init__(self):  
    
        self.items = []  
 
    def enqueue(self, item):  
        self.items.append(item)  
 
    def dequeue(self):  
        if not self.is_empty():  
            return self.items.pop(0)  
 
 
    def is_empty(self):  
        return len(self.items) == 0  
 
 
class Stack:  
    def __init__(self):  
        self.items = []  
 
    def push(self, item):  
        self.items.append(item)  
 
    def pop(self):  
        if not self.is_empty():  
 
  
 
            return self.items.pop()  
 
 
    def is_empty(self):  
        return len(self.items) == 0  
 
def reverse_queue(queue):  
    stack = Stack()  
 
    while not queue.is_empty():  
        element = queue.dequeue()  
        stack.push(element)  
 
 
    while not stack.is_empty():  
        element = stack.pop()  
        queue.enqueue(element)  
 
 
# Example usage:  
 
queue = Queue()  
 
queue.enqueue(15)  
queue.enqueue(12)  
queue.enqueue(33)  
queue.enqueue(54)  
queue.enqueue(65)  
 
 
reverse_queue(queue)
print("After reversing queue:")
while not queue.is_empty():  
    print(queue.dequeue())  

So, the Queue after reversing resulted in the following order: 65, 54, 33, 12, 15.

Finally, we have successfully reversed the Queue using a stack as an auxiliary data structure. To summarize, reversing a queue includes rearranging its members so that the first element becomes the last and vice versa. Reversing a queue can be beneficial in a variety of cases when components must be processed in a different order.

Next TopicDifferent Types of Stack Operations

← prev next →