Application of Linked List

In this article, we will understand the linked list applications in detail.

What do you mean by Linked list?

A linked list is a linear data structure consisting of elements called nodes where each node is composed of two parts: an information part and a link part, also called the next pointer part.

Linked list is used in a wide variety of applications such as

Polynomial Manipulation representation
Addition of long positive integers
Representation of sparse matrices
Addition of long positive integers
Symbol table creation
Mailing list
Memory management
Linked allocation of files
Multiple precision arithmetic etc

Polynomial Manipulation

Polynomial manipulations are one of the most important applications of linked lists. Polynomials are an important part of mathematics not inherently supported as a data type by most languages. A polynomial is a collection of different terms, each comprising coefficients, and exponents. It can be represented using a linked list. This representation makes polynomial manipulation efficient.

While representing a polynomial using a linked list, each polynomial term represents a node in the linked list. To get better efficiency in processing, we assume that the term of every polynomial is stored within the linked list in the order of decreasing exponents. Also, no two terms have the same exponent, and no term has a zero coefficient and without coefficients. The coefficient takes a value of 1.

Each node of a linked list representing polynomial constitute three parts:

The first part contains the value of the coefficient of the term.
The second part contains the value of the exponent.
The third part, LINK points to the next term (next node).

The structure of a node of a linked list that represents a polynomial is shown below:

Consider a polynomial P(x) = 7x² + 15x³ - 2 x² + 9. Here 7, 15, -2, and 9 are the coefficients, and 4,3,2,0 are the exponents of the terms in the polynomial. On representing this polynomial using a linked list, we have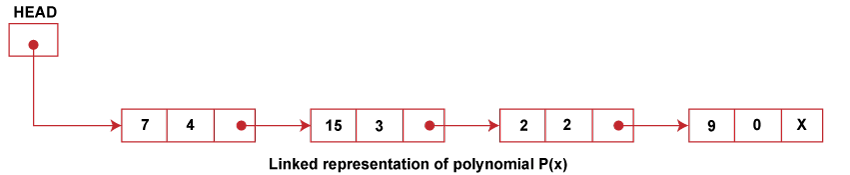

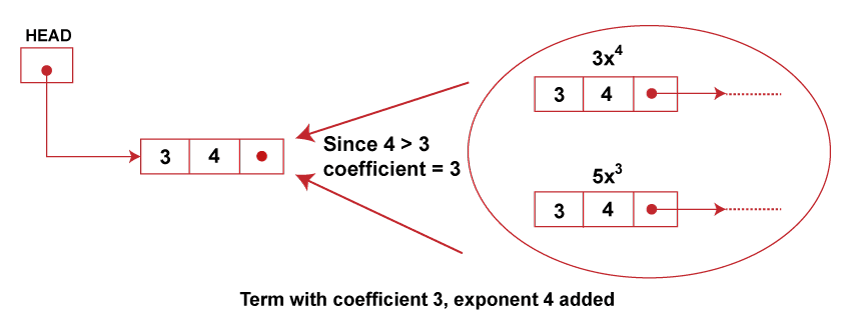
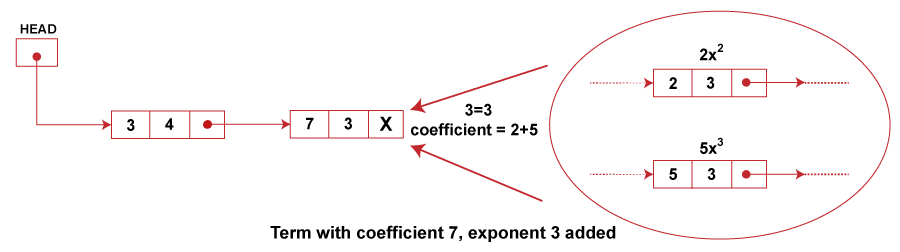
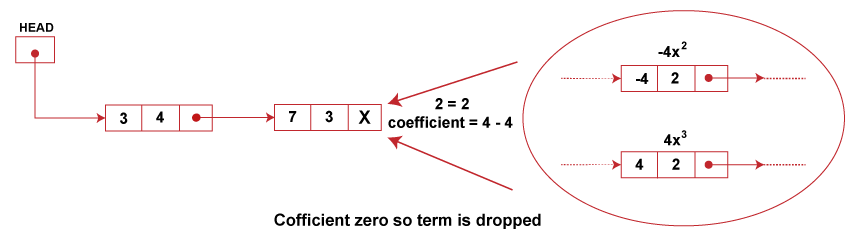
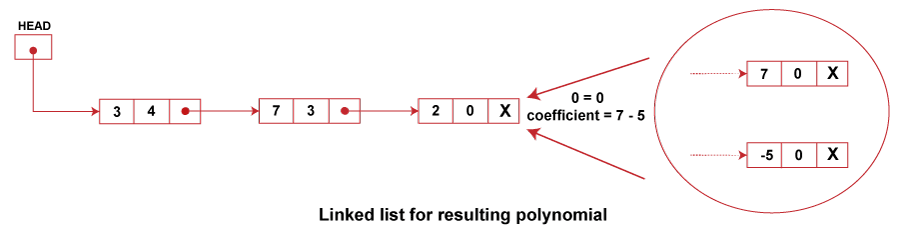
Observe that the number of nodes equals the number of terms in the polynomial. So we have 4 nodes. Moreover, the terms are stored to decrease exponents in the linked list. Such representation of polynomial using linked lists makes the operations like subtraction, addition, multiplication, etc., on polynomial very easy.

Addition of Polynomials:

To add two polynomials, we traverse the list P and Q. We take corresponding terms of the list P and Q and compare their exponents. If the two exponents are equal, the coefficients are added to create a new coefficient. If the new coefficient is equal to 0, then the term is dropped, and if it is not zero, it is inserted at the end of the new linked list containing the resulting polynomial. If one of the exponents is larger than the other, the corresponding term is immediately placed into the new linked list, and the term with the smaller exponent is held to be compared with the next term from the other list. If one list ends before the other, the rest of the terms of the longer list is inserted at the end of the new linked list containing the resulting polynomial.

Let us consider an example an example to show how the addition of two polynomials is performed,

P(x) = 3x⁴ + 2x³- 4 x² + 7

Q (x) = 5x³ + 4 x²- 5

These polynomials are represented using a linked list in order of decreasing exponents as follows: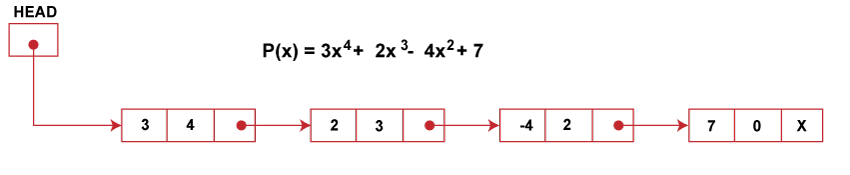

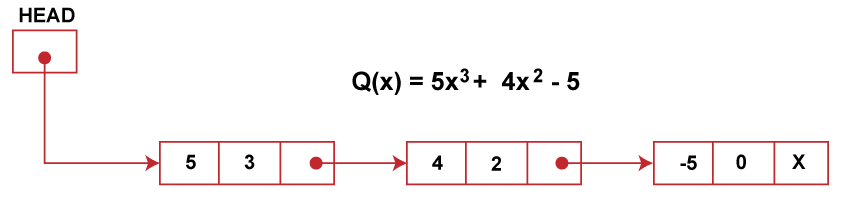
To generate a new linked list for the resulting polynomials that is formed on the addition of given polynomials P(x) and Q(x), we perform the following steps,

Traverse the two lists P and Q and examine all the nodes.
We compare the exponents of the corresponding terms of two polynomials. The first term of polynomials P and Q contain exponents 4 and 3, respectively. Since the exponent of the first term of the polynomial P is greater than the other polynomial Q, the term having a larger exponent is inserted into the new list. The new list initially looks as shown below:
We then compare the exponent of the next term of the list P with the exponents of the present term of list Q. Since the two exponents are equal, so their coefficients are added and appended to the new list as follows:
Then we move to the next term of P and Q lists and compare their exponents. Since exponents of both these terms are equal and after addition of their coefficients, we get 0, so the term is dropped, and no node is appended to the new list after this,
Moving to the next term of the two lists, P and Q, we find that the corresponding terms have the same exponents equal to 0. We add their coefficients and append them to the new list for the resulting polynomial as shown below:

Example:

C++ program to add two polynomials

#include <iostream>
using namespace std;
int max(int m, int n) { return (m > n)? m: n; }
int *add(int A[], int B[], int m, int n)
{
int size = max(m, n);
int *sum = new int[size];
for (int i = 0; i<m; i++)
	sum[i] = A[i];
for (int i=0; i<n; i++)
	sum[i] += B[i];
return sum;
}
void printPoly(int poly[], int n)
{
	for (int i=0; i<n; i++)
	{
	cout << poly[i];
	if (i != 0)
		cout << "x^" << i ;
	if (i != n-1)
	cout << " + ";
	}
}
int main()
{
	int A[] = { 5, 0, 10, 6 };
	int B[] = { 1, 2, 4 };
	int m = sizeof(A)/sizeof(A[0]);
	int n = sizeof(B)/sizeof(B[0]);
	cout << "First polynomial is \n";
	printPoly(A, m);
	cout << "\n Second polynomial is \n";
	printPoly(B, n);
	int *sum = add(A, B, m, n);
	int size = max(m, n);
	cout << "\n Sum of polynomial is \n";
	printPoly(sum, size);
	return 0;
}

Explanation:

In the above example, we have created an example of sum of two polynomial using array.

Output:

Below is the output of this example.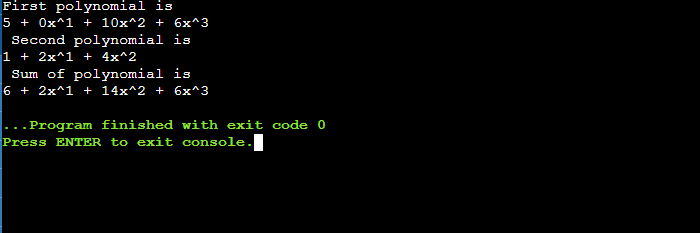

Addition of long positive integer using linked list

Most programming languages allow restrictions on the maximum value of integers stored. The maximum value of the largest integers is 32767, and the largest is 2147483647. Sometimes, applications such as security algorithms and cryptography require storing and manipulating integers of unlimited size. So in such a situation, it is desirable to use a linked list for storing and manipulating integers of arbitrary length.

Adding long positive integers can be performed effectively using a circular linked list. As we know that when we add two long integers, the digits of the given numbers are individually traversed from right to left, and the corresponding digits of the two numbers along with a carry from prior digits sum are added. So to accomplish addition, we must need to know how the digits of a long integer are stored in a linked list.

The digits of a long integer must be stored from right to left in a linked list so that the first node on the list contains the least significant digit, i.e., the rightmost digit, and the last node contains the most significant digit, i.e., leftmost digit.

Example: An integer value 543467 can be represented using a linked list as

For performing the addition of two long integers, the following steps need to be followed:

Traverse the two linked lists in parallel from left to right.
During traversal, corresponding digits and a carry from prior digits sum are added, then stored in the new node of the resultant linked list.

The first positive long integer 543467 is represented using a linked list whose first node is pointed by NUM1 pointer. Similarly, the second positive long integer 48315 is represented using the second linked list whose first node is pointed by NUM2 pointer. These two numbers are stored in the third linked list whose first node is pointed to by the RESULT pointer.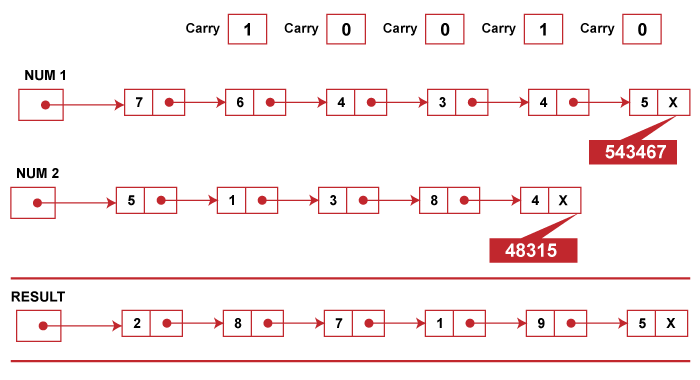

Example:

C++ program for addition of two polynomials using Linked Lists

#include <bits/stdc++.h>
#include <iostream.h>
using namespace std;
struct Node {
	int coeff;
	int pow;
	struct Node* next;
};
void create_node(int x, int y, struct Node** temp)
{
	struct Node *r, *z;
	z = *temp;
	if (z == NULL) {
		r = (struct Node*)malloc(sizeof(struct Node));
		r->coeff = x;
		r->pow = y;
		*temp = r;
		r->next = (struct Node*)malloc(sizeof(struct Node));
		r = r->next;
		r->next = NULL;
	}
	else {
		r->coeff = x;
		r->pow = y;
		r->next = (struct Node*)malloc(sizeof(struct Node));
		r = r->next;
		r->next = NULL;
	}
}
void polyadd(struct Node* poly1, struct Node* poly2,
			struct Node* poly)
{
	while (poly1->next && poly2->next) {
		if (poly1->pow > poly2->pow) {
			poly->pow = poly1->pow;
			poly->coeff = poly1->coeff;
			poly1 = poly1->next;
		}
		else if (poly1->pow < poly2->pow) {
			poly->pow = poly2->pow;
			poly->coeff = poly2->coeff;
			poly2 = poly2->next;
		}
		else {
			poly->pow = poly1->pow;
			poly->coeff = poly1->coeff + poly2->coeff;
			poly1 = poly1->next;
			poly2 = poly2->next;
		}
				poly->next
			= (struct Node*)malloc(sizeof(struct Node));
		poly = poly->next;
		poly->next = NULL;
	}
	while (poly1->next || poly2->next) {
		if (poly1->next) {
			poly->pow = poly1->pow;
			poly->coeff = poly1->coeff;
			poly1 = poly1->next;
		}
		if (poly2->next) {
			poly->pow = poly2->pow;
			poly->coeff = poly2->coeff;
			poly2 = poly2->next;
		}
		poly->next
			= (struct Node*)malloc(sizeof(struct Node));
		poly = poly->next;
		poly->next = NULL;
	}
}
void show(struct Node* node)
{
	while (node->next != NULL) {
		printf("%dx^%d", node->coeff, node->pow);
		node = node->next;
		if (node->coeff >= 0) {
			if (node->next != NULL)
				printf("+");
		}
	}
}
int main()
{
	struct Node *poly1 = NULL, *poly2 = NULL, *poly = NULL;
	create_node(5, 2, &poly1);
	create_node(4, 1, &poly1);
	create_node(2, 0, &poly1);
	create_node(-5, 1, &poly2);
	create_node(-5, 0, &poly2);
	printf("1st Number: ");
	show(poly1);
	printf("\n 2nd Number: ");
	show(poly2);
	poly = (struct Node*)malloc(sizeof(struct Node));
	polyadd(poly1, poly2, poly);
	printf("\n Sum of polynomial after addition: ");
	show(poly);
	return 0;
}

Explanation:

In the above example, we have created an example of sum of two polynomial using linked list.

Output:

Below is the output of this example.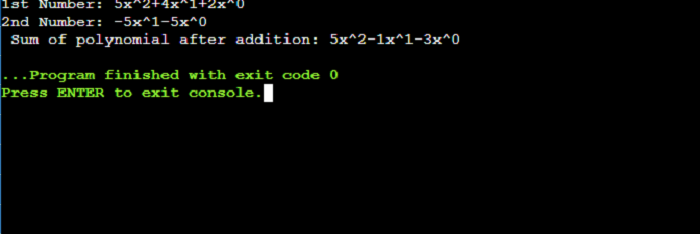

Polynomial of Multiple Variables

We can represent a polynomial with more than one variable, i.e., it can be two or three variables. Below is a node structure suitable for representing a polynomial with three variables X, Y, Z using a singly linked list.

Consider a polynomial P(x, y, z) = 10x²y²z + 17 x²y z² - 5 xy² z+ 21y⁴z² + 7. On represnting this polynomial using linked list are:

Terms in such a polynomial are ordered accordingly to the decreasing degree in x. Those with the same degree in x are ordered according to decreasing degree in y. Those with the same degree in x and y are ordered according to decreasing degrees in z.

Example

Simple C++ program to multiply two polynomials

#include <iostream>
using namespace std;
int *multiply(int A[], int B[], int m, int n)
{
int *prod = new int[m+n-1];
for (int i = 0; i<m+n-1; i++)
	prod[i] = 0;
for (int i=0; i<m; i++)
{
	for (int j=0; j<n; j++)
		prod[i+j] += A[i]*B[j];
}
return prod;
}
void printPoly(int poly[], int n)
{
	for (int i=0; i<n; i++)
	{
	cout << poly[i];
	if (i != 0)
		cout << "x^" << i ;
	if (i != n-1)
	cout << " + ";
	}
}
int main()
{
	int A[] = { 5, 0, 10, 6 };
	int B[] = { 1, 2, 4 };
	int m = sizeof(A)/sizeof(A[0]);
	int n = sizeof(B)/sizeof(B[0]);
	cout << "First polynomial is \n";
	printPoly(A, m);
	cout << "\nSecond polynomial is \n";
	printPoly(B, n);
	int *prod = multiply(A, B, m, n);
	cout << "\nProduct of two polynomial is \n";
	printPoly(prod, m+n-1);
	return 0;
}

Explanation:

In the above example, we have created an example of multiple of two polynomial using arrays.

Output:

Below is the output of this example.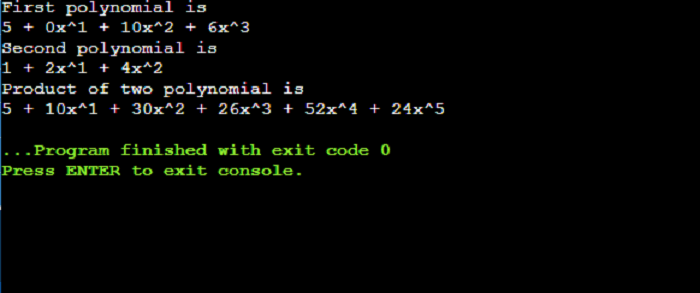

Some other applications of linked list:

Memory Management: Memory management is one of the operating system's key features. It decides how to allocate and reclaim storage for processes running on the system. We can use a linked list to keep track of portions of memory available for allocation.
Mailing List: Linked lists have their use in email applications. Since it is difficult to predict multiple lists, maybe a mailer builds a linked list of addresses before sending a message.
LISP: LISP is an acronym for LIST processor, an important programming language in artificial intelligence. This language extensively uses linked lists in performing symbolic processing.
Linked allocation of files: A file of large size may not be stored in one place on a disk. So there must be some mechanism to link all the scattered parts of the file together. The use of a linked list allows an efficient file allocation method in which each block of a file contains a pointer to the file's text block. But this method is good only for sequential access.
Virtual Memory: An interesting application of linked lists is found in the way systems support virtual memory.
Support for other data structures: Some other data structures like stacks, queues, hash tables, graphs can be implemented using a linked list.

Next TopicTopological Sorting

← prev next →