Symmetric Binary Tree

Each node has a left and a right subtree in a binary tree. Any binary tree, including empty, single-node trees, and subtrees, can exist. If the right subtree and the left subtree of the root node are mirror images of each other, then a binary tree is said to be symmetric.

Validate whether a binary tree is a mirror of itself if one is provided.

For illustration, the binary tree below is symmetric: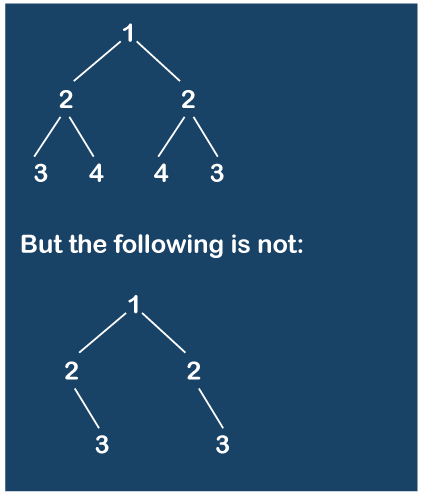

The goal is to create a recursive method called isMirror() that accepts two arguments of trees and returns true if the two trees are the mirror and false otherwise. Recursively examining two roots and subtrees beneath the root is the isMirror() method.

Approach:

The following is a concise summary of the algorithmic steps:

We start out with two variables, root1 and root2, both of which point to the root.
The nodes are then traversed using any tree traversal method. In this traversal function, we will simultaneously alter root1 and root2.
In the base scenario, we return true if both are referring to NULL, but we return false if just one is pointing to NULL and the other is pointing to a node.
We initially compare the values of any two points that point to the same node, and if they are equal, we look at the lower levels of the tree.
Recursively calling the function checks the left child of the root1 with the right child of the root2, and then checks the right child of the root1 with the left child once again.
We return true from our function if all three conditions-the node values of the left and right and the two recursive calls-are satisfied, otherwise we return false.

The aforesaid algorithm is implemented in the manner shown below.

C Program:

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
	int key;
	struct Node *left, *right;
} Node;

Node* newNode(int key)
{
	Node* temp = (Node *)malloc(sizeof(Node));
	temp -> key = key;
	temp -> left = temp -> right = NULL;
	return (temp);
}

bool isMirror(Node* root1, Node* root2)
{
	if (root1 == NULL && root2 == NULL)
		return true;
 
	if (root1 && root2 && root1 -> key == root2 -> key)
		return isMirror(root1 -> left, root2 -> right)
			&& isMirror(root1->right, root2->left);

	return false;
}
bool isSymmetric(Node* root)
{
	return isMirror(root, root);
}

int main()
{

	Node* root = newNode(1);
	root -> left = newNode(2);
	root -> right = newNode(2);
	root -> left -> left = newNode(3);
	root -> left -> right = newNode(4);
	root -> right -> left = newNode(4);
	root -> right -> right = newNode(3);

	if (isSymmetric(root))
		printf("Symmetric");
	else
		printf("Not symmetric");
	return 0;
}

Output:

Symmetric

C++ Program:

#include <bits/stdc++.h>
using namespace std;

struct Node {
	int key;
	struct Node *left, *right;
};

Node* newNode(int key)
{
	Node* temp = new Node;
	temp -> key = key;
	temp -> left = temp -> right = NULL;
	return (temp);
}

bool isMirror(struct Node* root1, struct Node* root2)
{
	if (root1 == NULL && root2 == NULL)
		return true;

	if (root1 && root2 && root1 -> key == root2 -> key)
		return isMirror(root1 -> left, root2 -> right)
			&& isMirror(root1 -> right, root2 -> left);

	return false;
}

bool isSymmetric(struct Node* root)
{
	return isMirror(root, root);
}
int main()
{

	Node* root = newNode(1);
	root -> left = newNode(2);
	root -> right = newNode(2);
	root -> left -> left = newNode(3);
	root -> left -> right = newNode(4);
	root -> right -> left = newNode(4);
	root -> right -> right = newNode(3);

	if (isSymmetric(root))
		cout << "Symmetric";
	else
		cout << "Not symmetric";
	return 0;
}

Output: