Find an element in array such that sum of the left array is equal to the sum of the right array

We are given an array of n elements, and we have to find that element in the array, which divides the array into two parts in such a way, that the sum of both subarrays is equal. Basically, the sum of the left side and the right side is equal to that element. If there is no such kind of element present, then we will return -1.

For example:

Array={5,-1,4,6,12,0,-4}

In the above array, element 6 is that array which divides the array into an equal sum size subarray.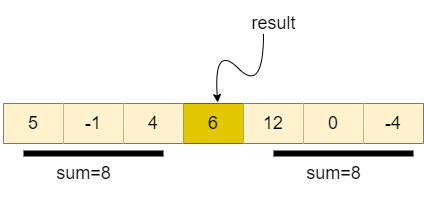

Method1

The bruteforce approach to solve the problem is that we will consider every element as a partition element and calculate the left side and right side sum. If the sum is equal, we will return it. Otherwise, we will move to the next element.

Java code:

Output:

Time complexity: O(N²)

Space complexity: O(1)

Method2

The optimized approach for the above problem is that we can use prefix and suffix array to store the result of the array for the left side and the right side.

Java code:

Output:

Time complexity: O(3*N)~ O(N)

Space complexity: O(N+N)~O(N)

Method 3

We can use constant space for solving this problem. We will get the sum of the array and make it the right sum, and we will take the left sum as zero. Now for every element, we will consider it as a partition element, so we will decrease the value in the right sum and then check the left sum and right sum.

If both are equal, we will change the answer. Otherwise, we will add the element to the left sum.

Java code:

Output:

Explanation

Initially, we have two variables, left_sum and right_sum, and both are zero. We store the sum of all elements into the variable right_sum, which is 19 for the above example.

Now when i=0, we will subtract arr[0] from right_sum to get the sum of elements to the RHS of arr[0].

So right_sum=17 and left_sum =0. Since both are not equal, we will move ahead, but for the next value current value should be added as left_sum.so left_sum =2.

For i=1, now right_sum=17 we will subtract arr[1], so right_sum=14 which is the sum of RHS value of arr[1] and now left_sum=2 and both are not equal, so move ahead and before that add current value in left_sum.

So left_sum =5 and right_sum=14.

For i=2 right_sum=14 - 4 = 10 and left_sum = 5. Both are not equal so left_sum=5+4 = 9.

For i=3 right_sum=10-1 = 9 and left_sum = 9 , since both are same and current element is our answer so we will update our result.

result=arr[3]=1.

Time complexity: O(N)

Space complexity: O(1)

Method 4

We can use a two-pointers approach, but the elements should be positive. We will use i=0 and j=n-1, and we will do the traversal from the left and right sides.

• If left_sum and right_sum are equal and i<j, then we will add arr[i] to left_sum and arr[j] to the right_sum, and we will increase i by one and decrease j by 1.
• If left_sum and right_sum is equal and i==j we will store the result as arr[i].
• If left_sum<right_sum then we will add arr[i] to left_sum and increase i by 1.
• If right_sum<left_sum then we will add arr[j] to right_sum and decrease j by 1.

Java code:

Output:

Time complexity: O(N)

Space complexity: O(1)