The non-overlapping sum of two setsLet us understand the question with a suitable example: Let us assume two sets as, s1={1,2,3,4}, s2={3,4,5,6} In the above two sets, we need to find out the elements that are not common in both. In set s1, we have 3,4, which are also repeated in the s2 set, so 3,4 are the elements not to be considered. If we remove 3,4 elements, the remaining elements are 1,2,5,6. Let us take another example, if the sets are s1={5,6,7,8} and second set s2={9,10,11,12} In the above two sets, no elements in set 1 are in common with the elements of set 2. So, no elements were repeated. Now, we need to write a code to find out the numbers that are not repeated and print them. First, let us discuss the brute force approach for this solution. CODE: Output: 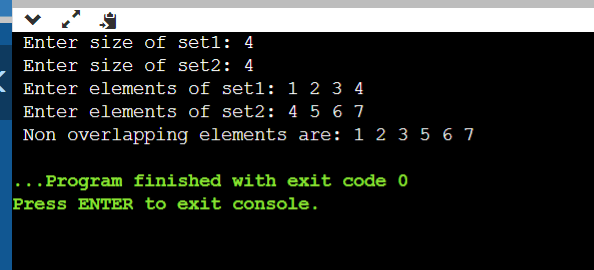
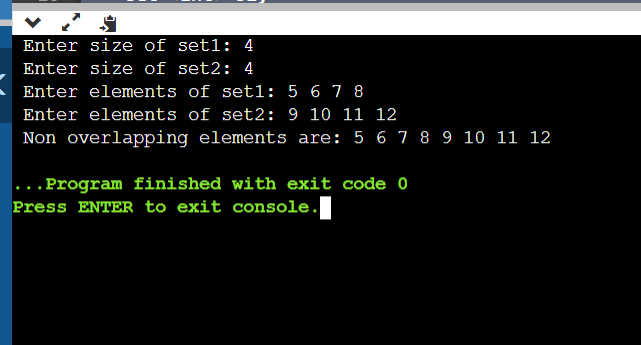
Let us discuss the working of the code: First, we need to take the input for the size of the two sets and the elements of the two sets. The above lines of code will take input for both the sizes of sets and the elements of both sets. After taking the input, we need to find out the non-overlapping elements of the two sets. How do we find the non-overlapping elements? It is simple to find the overlapping elements, i.e., for an element in set 1, we need to search for that element in the entire second set, i.e., set 2. Let us understand this using an example: If set1 is {1,2,3,4} and second set is {3,4,5,6} Now, for every element in set 1, i.e., let's start from 1, and we need to check if 1 is present in the second set or not. And 1 is not present in the second set, so 1 is a non-overlapping element, so we print the value. Similarly, we need to check for the element of set1 in the set2. Next, we have 3, and we will check whether 3 is present in the second set. It is present in the set, so it is an overlapping element and doesn't print the element. After completing all the elements of set1, we need to check for all the elements of set2, whether they are present in the set1. (As we have done previously for set 1). After completing the above two sets, all the non-overlapping elements will finally be printed. To find out the over-lapping elements, we have written a function called non_over: The above function is responsible for printing all the non-overlapping elements of set1 and set2. Let us discuss the time and space complexities: Time complexity: if we ignore the time taken for taking the input. For every element in s1, we are searching for every element in s2, sot the time taken is n1*n2, and we perform it twice, so 2*n1*n2. We consider it as n1*n2. If we consider n1=n2=n then the time complexity is: O(n*2) Space complexity: We haven't used space here, so space complexity remains constant. i.e., O(1). Since the time complexity is O(N*2), we need to optimize the code, So, let us discuss another approach: In this approach, we will use a hashmap to store the values of two sets. Since the map stores the two values as key and value pairs, we can easily maintain the count of every element of both sets. i.e., if an element is already present in the map, we increment its count. Otherwise, we will add the element and make the count to 1. We will push the elements into the map while taking the input, so all values will be pushed into the map while taking the input. To find out the non-overlapping elements of two sets, the elements are nothing but those with the count value of 1. i.e., whatever element counts as 1 is considered a non-overlapping element. So, we need to deploy a code that inserts values into the amp while taking the input and prints the non-overlapping elements of the two sets. CODE: Output: 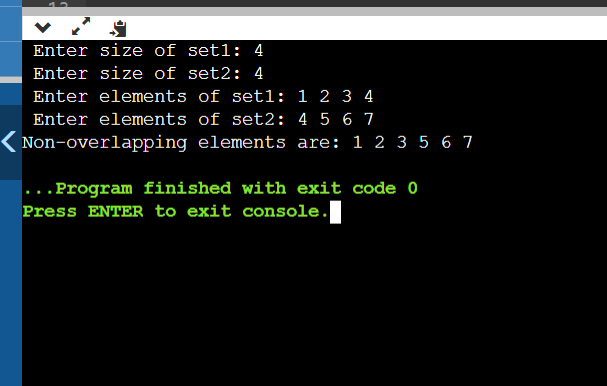
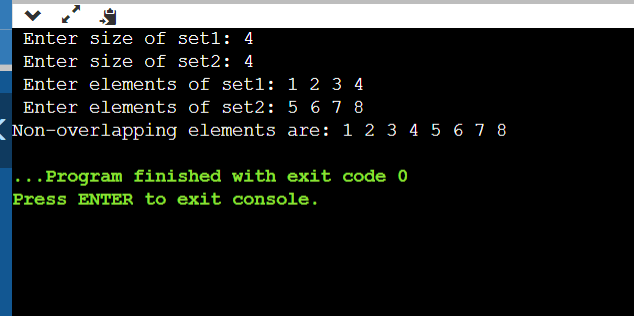
EXPLANATION: The only change from the previous code is using the map here. We have inserted values into the map named mp. How have we inserted it?Using mp[x]++, the values will be inserted into the map; if the value is not present, a new value will be inserted, and the counter will be incremented. Now, we need to print the map's values where the count value is 1 because if the count is 1, only it is said to be a non-overlapping element. Above is the function which prints the non-overlapping elements. i.e., we check if it. The second is 1; then, we will print the values. Otherwise, we ignore the element. So, this is how we will print the non-overlapping elements of two sets. Let us discuss the time and space complexity of the code: Time complexity: If we ignore the time taken to take the input, we need time to print the non-overlapping elements of two sets. The time taken for it is the map's size, and the maximum size of the map can be n1+n2, so the time complexity is O(n1+n2) in the worst case. Space complexity: The space required for this code is a map. we need a map to store the elements of both sets, so the size of set1 is n1, and the size of set2 is n2 to the total space taken is O(n1+n2) Time complexity: O(n1+n2) Space complexity: O(n1+n2) From the previous approach, we can see that we have decreased the time complexity from O(N1*N2) to O(N1+N2) And the space complexity is changed from O(1) to O(N1+N2)
Next TopicPalindrome substring queries
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









