Intersection of Linked List

Introduction

Linked lists are fundamental data structures in computer science, widely used to store and manage collections of data. One intriguing operation involving linked lists is finding their intersection - the point at which two linked lists share common nodes. This seemingly simple task has numerous real-world applications and requires the application of clever algorithms to achieve efficient solutions.

Understanding Linked Lists

Before diving into the intricacies of finding the intersection, let's briefly recap what linked lists are. A linked list is a linear data structure consisting of nodes, where each node contains data and a reference (or pointer) to the next node in the sequence. This structure allows for dynamic memory allocation and efficient insertion or removal of elements from the list.

Linked lists come in different flavors: singly linked lists, doubly linked lists, and circular linked lists. The structure of the list impacts how we approach finding intersections.

The Intersection Problem

Given two linked lists, the intersection is defined as the node where the two lists meet. This can happen due to the lists sharing a common portion, often referred to as the "tail." Prior to this intersection, the lists are distinct and might have different lengths.

The challenge is to determine if the linked lists intersect and, if so, identify the node at which the intersection occurs. This seemingly straightforward task becomes complex when considering lists of varying lengths and structures.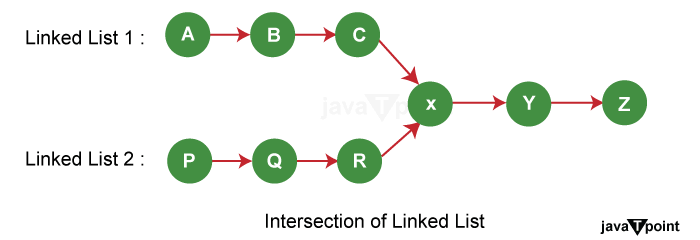

Detecting the Intersection

Detecting an intersection between two linked lists involves finding the node where the lists converge. This can be achieved through various algorithms, one of which is the "two-pointer" approach. Here's how it works:

1. Initialize Pointers: Start with two pointers, one for each linked list. Traverse both lists simultaneously, moving one step at a time.
2. Advance the Pointers: As long as the pointers are not null, keep moving them forward. If one pointer reaches the end of its list, move it to the head of the other list. This balances the difference in list lengths.
3. Intersection Detection: If the two pointers meet at a common node (i.e., they point to the same memory location), you have found the intersection point. Return that node.

This algorithm works because the combined steps taken by both pointers are equal, whether the lists have an intersection or not. If there's an intersection, the pointers will eventually meet at the common node. If there's no intersection, they will both reach the end (null) simultaneously.

Approaches to Finding Intersections

Several approaches exist to tackle the intersection problem, each with varying time and space complexities. Here are two common methods:

Brute Force Method:

The simplest way to solve this problem is by iterating through one list and, for each node, iterating through the second list to check for matching nodes. While this approach works, it has a time complexity of O(m * n), where m and n are the lengths of the two linked lists, making it highly inefficient for large lists.

Hashing:

In this approach, we can store the nodes of the first linked list in a hash table. Then, while traversing the second linked list, we check if the current node exists in the hash table. This approach reduces the time complexity to O(m + n), where m and n are the lengths of the two linked lists. However, it requires additional space for the hash table.

Two-Pointer Approach:

The most efficient approach involves utilizing two pointers that traverse both linked lists. Start by simultaneously traversing both lists until the end is reached. When one list reaches the end, redirect it to the head of the other list. Continue traversing until the two pointers meet; this will be the intersection point. This approach has a time complexity of O(m + n) and doesn't require any additional data structures.

Implementation:

Explanation:

• The ListNode struct represents a node in the linked list.
• The findIntersection function takes two pointers to linked list heads, headA and headB, as input. It aims to find the node where the two linked lists intersect. The function utilizes a concept based on two runners moving through the linked lists. It initializes runnerA and runnerB to the respective heads of the input linked lists.
• The loop within the findIntersection function continues until runnerA and runnerB point to the same node (the intersection point) or both runners reach the end of their respective lists.
• In each iteration, runnerA and runnerB are moved to the next node. If runnerA reaches the end of its list, it is reset to the head of the other linked list (headB), and vice versa. This way, the runners will eventually meet at the intersection point or become nullptr if there is no intersection.
• In the main function, two linked lists listA and listB are constructed with sample values. An intersection is created by making the last node of listB point to the second node of listA.
• The findIntersection function is then called with listA and listB as arguments to determine the intersection point.
• If an intersection is found (the runners meet), the value of the intersection node is printed. Otherwise, a message indicating no intersection is printed.

Program Output:

Optimized Approach: Two Pointers

The most efficient approach, often referred to as the "Two Pointers" method, involves utilizing two pointers that traverse the linked lists simultaneously. This approach leverages the difference in lengths between the two lists to ensure that the pointers meet at the intersection point.

1. Initialize two pointers, one for each linked list.
2. Traverse both linked lists, moving each pointer one node at a time.
3. When a pointer reaches the end of its list, redirect it to the head of the other list.
4. Repeat the traversal until the pointers meet. The meeting point is the intersection.

This approach has a time complexity of O(m + n) and does not require additional space, making it a highly efficient solution.

Applications of Linked List Intersection

The intersection of linked lists has various applications in computer science and beyond:

Memory Management: In memory management systems, identifying shared memory areas between different processes can help optimize resource allocation.

Cycle Detection: Linked lists are used to detect cycles in networks, such as in graph theory, and finding the intersection can assist in identifying common nodes.

Collision Detection: In computer graphics and gaming, linked lists can represent objects in a scene. Intersections can be used to detect collisions between these objects.

Route Optimization: In geographic information systems, linked lists can represent road networks. Identifying intersections helps find optimal routes.

Database Management: In database systems, linked list intersections are used to efficiently retrieve common records from multiple tables based on shared attributes. This optimizes query performance by minimizing the need for exhaustive comparisons.

Traffic Flow Analysis: Imagine two streets representing linked lists. At the point where they intersect, we could analyze traffic patterns, congestion, and other variables. This helps urban planners make informed decisions about traffic management.

Conclusion:

The intersection of linked lists is a common problem in computer science and algorithm design. Efficiently finding the intersection point is essential for various applications, including finding common elements in datasets, cycle detection in linked lists, and more.

By understanding the principles of linked lists and employing algorithms like the two-pointer approach, programmers can efficiently solve the intersection problem and optimize their code for better performance.

Solving the intersection of linked lists efficiently requires careful consideration of the data structures and algorithms involved. One common approach is to traverse both linked lists simultaneously, maintaining pointers or indices to track their positions. By identifying the point where the two lists converge, the intersection can be found.

In some cases, the use of additional data structures, such as hash sets or marking nodes, can help expedite the process of detecting intersections. However, the choice of approach depends on the characteristics of the linked lists and the specific requirements of the problem.