PERMUTED ROWS IN A MATRIX

Introduction:

The field of matrix manipulation and permutation plays an important role in a variety of fields, from computer science to computational biology. Finding modified rows in a matrix is an interesting endeavor that reveals the complexity of patterns and relationships embedded in data structures. In this talk, we embark on a journey to understand the methods and procedures for finding modified characters, as shown in the picture below.

A matrix, a two-dimensional set of numbers or symbols, is a basic structure in mathematical calculations. The concept of change-a particular sequence of objects-reveals many possibilities in the matrix field. The task of detecting and extracting all modified lines from an image requires displaying a band of modifications in the line. At the core of this insight is the essence of combining science with algorithmic efficiency.

Combinatorics, a mathematical branch of object computation and processing, provides a theoretical basis for understanding the number of possible permutations of a matrix. Still, the challenge lies in designing algorithms that can efficiently navigate and consider these permutations in large matrices.

The main way to solve this puzzle is to exploit the power of permutation sets and to use permutation algorithms. Variability groups allow the ordering and classification of variables within a matrix and enable the systematic examination of possible arrangements.

Algorithmic methods ranging from brute-force methods to more sophisticated heuristics emerge to navigate the matrix landscape and identify which rows have been modified correctly. Searching for modified rows in a matrix provides practical applications in a variety of fields, such as data analysis, image processing, and cryptography.'

For example, finding modified rows in data analysis can reveal hidden patterns or relationships that can be important for informed decision-making. Understanding modified dimensions in image processing can help with tasks such as image recognition and feature extraction. Furthermore, the study of cryptographic manipulation is an important part of developing secure encryption algorithms.

As we delve deeper into the complex world of matrix permutations, we will unpack complexity, explore algorithmic innovations, and consider the importance of these efforts in the broader computer science landscape.

Approach for implementation

For this problem, we're going to use a hash set to find the result. Originally, we will store the given row whose permutations are going to be set up in the HashSet; after this, we will cut over the given matrix to find the permuted rows except for the given row. In the covering, we will check whether the rudiments in each row are present in the HashSet or not. However, we will publish the row number on the press if all that row is present in the hash set.

Algorithm for the implementation

• Start.
• Declare the size of the matrix mxn and the row number whose permutation we need to find.
• Declare the 2-d matrix.
• publish the matrix and row number on the press
• Initialize the hash set for the problem.
• Fit the given row into the hash set.
• Reiterate in a nested circle of m and n to find the permuted row.
• Ignore the replication if the given row number and current row are the same.
• After changing the permuted row, print it on the press.
• End.

Implementation of the program

Output:

The output of the above program is: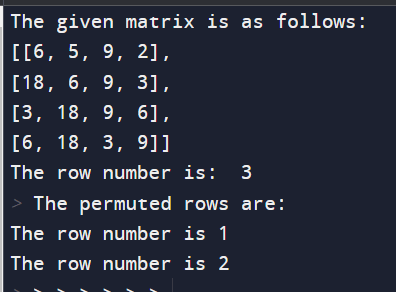

Explanation:

A Python function parses a matrix to display and print a row of permutations of the specified row. Numbers with dimensions of 4x4 are represented as a list. The focus is on finding rows with permutations of rows indexed by `r` (row 3 in this case).

A hash set (`s`) is used to facilitate efficient element comparison. The set is populated with unique items in the row shown, providing a basis for identifying variables. The function iterates through each row of the matrix (except for the specified row, `r`).

For each row, it compares the elements with those in the hash set. If there is a mismatch, the loop is broken, which means that the current line has no permutation. If the loop terminates without breaking, the row is considered a permutation, and its index is printed. The program imports the initial matrix and the specified row number (`r`) and then prints the indices of the rows containing the permutations of the specified row.

This scheme provides a useful way to identify modified rows in a matrix using a set of hashes for efficient element comparison. Although specific to a given line, it lays the foundation for further research on permutation-related algorithms and optimization in the context of matrix manipulation.

Complexities:

The Python function handed aims to render a modified row in a matrix grounded on a specified row, using a set of hashes for more effective element comparisons. We look for tight timing and space in the program.

Time complexity

The time complexity of the program is determined by nested circles that repeat through the rows and columns of the matrix. The external thread iterates through each row, and the inner circle iterates over each element in the row. Since there are two nested circles, the time complexity is O(rows * couloirs), where rows are the number of rows in the matrix, and couloirs are the number of columns. In the inner circle, conduct is similar, as set additions, subscription checks, and print statements are constant.

Therefore, it only significantly affects the overall time complexity. Still, the set addition operation is performed only once in a particular row, always contributing to the time constraint. In summary, the time complexity is direct with respect to the size of the matrix, making it O (rows * columns).

Space Complexity

The position complexity of the process is affected by the hash set(s) used to store the unique objects on the specified line. In the worst case, where all particulars in a row are unique, the space complexity is O(couloirs), where couloirs are the number of columns of the matrix. In addition to the hash set, the program uses several integer variables to control the circle, which only supports constant space.

Therefore, the overall spatial complexity is dominated by the size of the hash set. In conclusion, the spatial complexity is direct with respect to the number of columns in the matrix, performing in O(couloirs) spatial complexity. On the face of it, the program is effective in terms of the complexity of time and space.

In practical terms, the program is effective in terms of both time and space complications. It efficiently identifies permuted rows using a hash set, making it suitable for small to relatively large matrices. For larger matrices or scripts with strict performance conditions, further optimizations might be considered.

Method-2

Output:

The output of the above program is: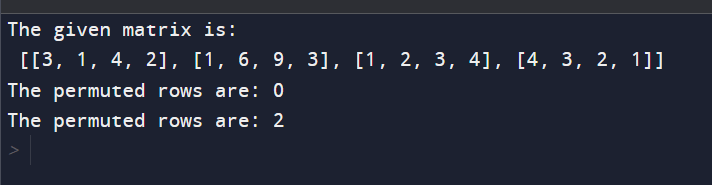

Explanation:

The handed Python program identifies permuted rows in a matrix with respect to a specified row' r.' It utilizes a hash set to count the frequentness of rudiments in the given row efficiently' r.' The program also traverses through the remaining rows, comparing their element frequency with those in the hash set. However, the row is considered a permutation, and its indicator is published; if the frequentness matches in the given illustration matrix of confines 4x4, with' r' as 3, the program labors the indicators of permuted rows. This perpetration offers a clear and terse approach to chancing permuted rows, demonstrating the effective use of sets and nested circles.