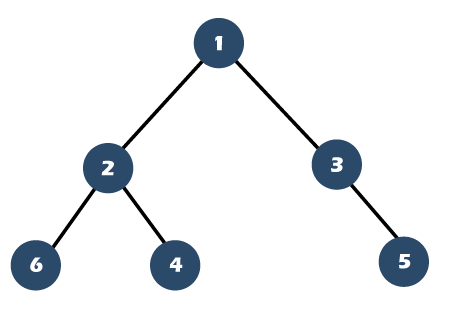
Full Binary Tree vs. Complete Binary Tree

What is a Full binary tree?

A full binary tree can be defined as a binary tree in which all the nodes have 0 or two children. In other words, the full binary tree can be defined as a binary tree in which all the nodes have two children except the leaf nodes.

The below tree is a full binary tree: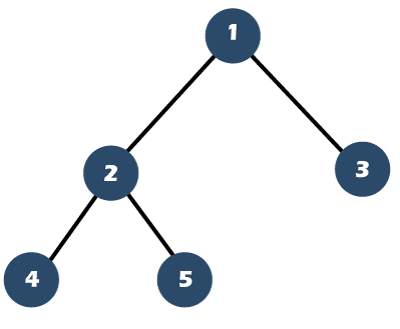

The above tree is a full binary tree as all the nodes except the leaf nodes have two children.

Full Binary tree theorem:

Consider a Binary tree T to be a nonempty tree then:

• Let I be internal nodes in a tree and L to be a leaf node in a tree, then the number of leaf nodes would be equal to:
  L = I + 1
• If T has, I number of internal nodes and N to be the total number of nodes, then the total number of nodes would be equal to:
  N = 2I + 1
• If T contains 'N' total number of nodes and 'I' to be number of internal nodes, then the number of internal nodes would be equal to:
  I = (N-1)/2
• If 'T' has 'N' total number of nodes, and 'L' to be a number of leaf nodes, then the number of leaf nodes would be equal to:
  L = (N+1)/2
• If 'T' contains 'L' number of leaf nodes, then the total number of nodes would be equal to:
  N = 2L - 1
• If 'T' has 'L' number of leaf nodes, and 'I' to be a number of internal nodes, then the number of internal nodes would be equal to:
  I = L - 1

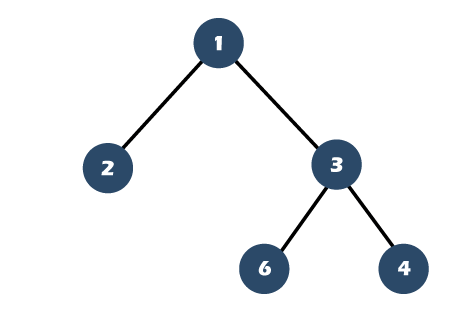
What is a complete binary tree?

A binary tree is said to be a complete binary tree when all the levels are completely filled except the last level, which is filled from the left.

The below tree is a complete binary tree: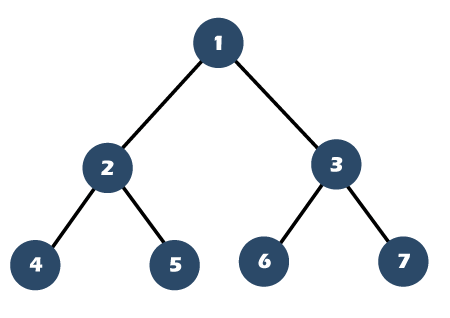

The complete binary tree is similar to the full binary tree except for the two differences which are given below:

• The filling of the leaf node must start from the leftmost side.
• It is not mandatory that the last leaf node must have the right sibling.

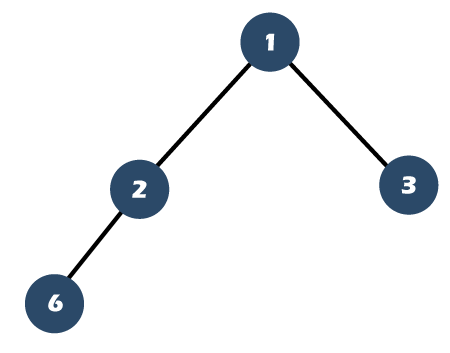
Let's understand the above points through an example:

Consider the below tree: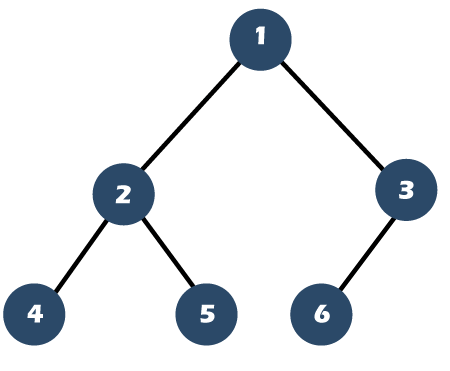

The above tree is a complete binary tree, but not a full binary tree as node 6 does not have its right sibling.

Creation of Complete Binary Tree

Suppose we have an array of 6 elements shown as below:

The above array contains 6 elements, i.e., 1, 2, 3, 4, 5, 6. The following are the steps to be used to create a complete binary tree:

Step 1: First, we will select the first element of the array, i.e., 1, and make a root node of the tree. The number of elements available in the first level is 1.

Step 2: Now, we will select the second and third elements of the array. Keep the second element and third element of the array as the left and right child of the root node respectively shown as below: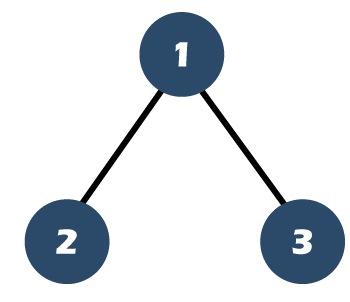

As we can observe above that the number of elements available in the second level is 2.

Step 3: Now, we will select the next two elements from the array, i.e., 4 and 5. Keep these two elements on the left and right of node 2 shown as below: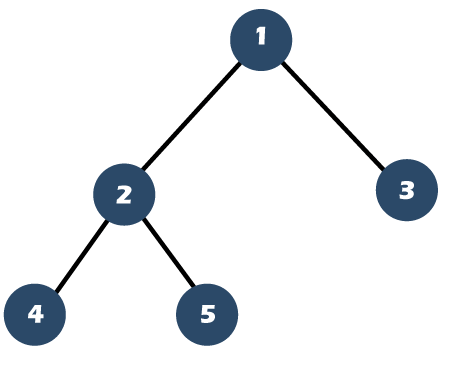

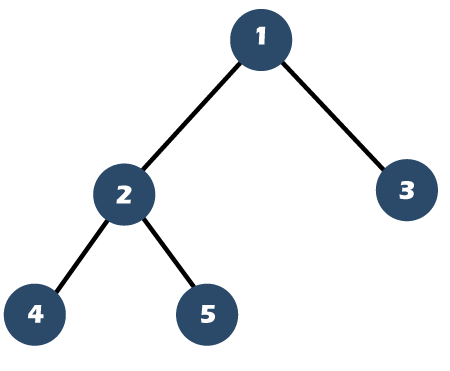
As we can observe above that nodes 4 and 5 are the left and right child of node 2 respectively.

Step 4: Now, we will select the last element of the array, i.e., 6, and keep it as left child of the node 3 as we know that in a complete binary tree, the nodes are filled from the left side shown as below: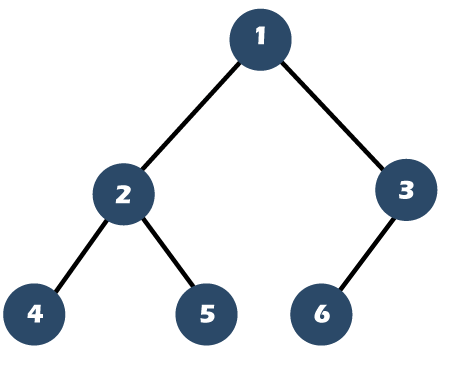

As we can observe that the second level contains 3 elements.

Let's understand the differences between complete and full binary tree through the images.

1. The binary tree which is shown below is neither a complete nor a full binary tree. It is not a full binary tree because node 3 has only one child. It is also not a complete binary tree as the nodes should be filled from the left side, but node 3 has a right child and does not have a left child.
   
2. The binary tree, which is shown below, is a full binary tree but not a complete binary tree. It is a full binary tree because all the nodes have either 0 or 2 children. It is not a complete binary tree because node 3 does not have any children while node 2 has its children and we know that the nodes should be filled from the left side in a complete binary tree.
   
3. The binary tree which is shown below is a complete binary tree but not a full binary tree. It is a complete binary tree as all the nodes are left filled. It is not a full binary tree as node 2 has only one child.
   
4. The binary tree which is shown below is a complete as well as a full binary tree. It is a complete binary tree as all the nodes are left filled. It is a full binary tree as all the nodes have either 0 or 2 children.