Graph representation

In this article, we will discuss the ways to represent the graph. By Graph representation, we simply mean the technique to be used to store some graph into the computer's memory.

A graph is a data structure that consist a sets of vertices (called nodes) and edges. There are two ways to store Graphs into the computer's memory:

Sequential representation (or, Adjacency matrix representation)
Linked list representation (or, Adjacency list representation)

In sequential representation, an adjacency matrix is used to store the graph. Whereas in linked list representation, there is a use of an adjacency list to store the graph.

In this tutorial, we will discuss each one of them in detail.

Now, let's start discussing the ways of representing a graph in the data structure.

Sequential representation

In sequential representation, there is a use of an adjacency matrix to represent the mapping between vertices and edges of the graph. We can use an adjacency matrix to represent the undirected graph, directed graph, weighted directed graph, and weighted undirected graph.

If adj[i][j] = w, it means that there is an edge exists from vertex i to vertex j with weight w.

An entry A_ij in the adjacency matrix representation of an undirected graph G will be 1 if an edge exists between V_i and V_j. If an Undirected Graph G consists of n vertices, then the adjacency matrix for that graph is n x n, and the matrix A = [aij] can be defined as -

a_ij = 1 {if there is a path exists from V_i to V_j}

a_ij = 0 {Otherwise}

It means that, in an adjacency matrix, 0 represents that there is no association exists between the nodes, whereas 1 represents the existence of a path between two edges.

If there is no self-loop present in the graph, it means that the diagonal entries of the adjacency matrix will be 0.

Now, let's see the adjacency matrix representation of an undirected graph.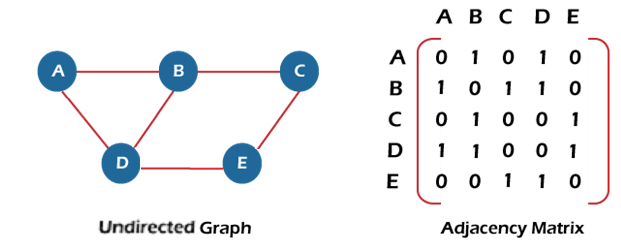

In the above figure, an image shows the mapping among the vertices (A, B, C, D, E), and this mapping is represented by using the adjacency matrix.

There exist different adjacency matrices for the directed and undirected graph. In a directed graph, an entry A_ij will be 1 only when there is an edge directed from V_i to V_j.

Adjacency matrix for a directed graph

In a directed graph, edges represent a specific path from one vertex to another vertex. Suppose a path exists from vertex A to another vertex B; it means that node A is the initial node, while node B is the terminal node.

Consider the below-directed graph and try to construct the adjacency matrix of it.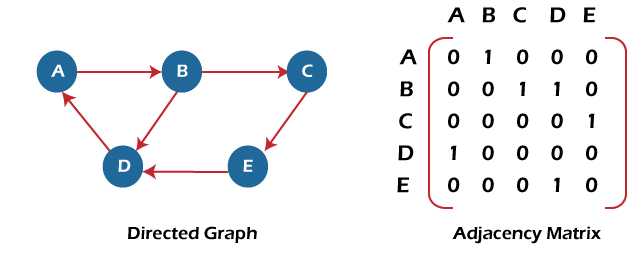

In the above graph, we can see there is no self-loop, so the diagonal entries of the adjacent matrix are 0.

Adjacency matrix for a weighted directed graph

It is similar to an adjacency matrix representation of a directed graph except that instead of using the '1' for the existence of a path, here we have to use the weight associated with the edge. The weights on the graph edges will be represented as the entries of the adjacency matrix. We can understand it with the help of an example. Consider the below graph and its adjacency matrix representation. In the representation, we can see that the weight associated with the edges is represented as the entries in the adjacency matrix.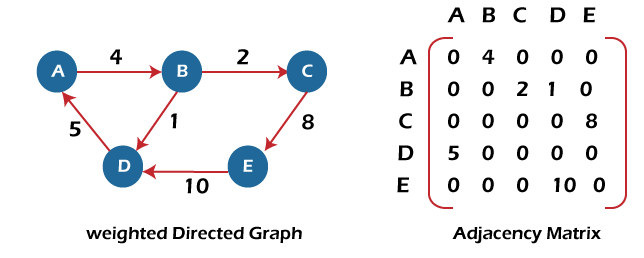

In the above image, we can see that the adjacency matrix representation of the weighted directed graph is different from other representations. It is because, in this representation, the non-zero values are replaced by the actual weight assigned to the edges.

Adjacency matrix is easier to implement and follow. An adjacency matrix can be used when the graph is dense and a number of edges are large.

Though, it is advantageous to use an adjacency matrix, but it consumes more space. Even if the graph is sparse, the matrix still consumes the same space.

Linked list representation

An adjacency list is used in the linked representation to store the Graph in the computer's memory. It is efficient in terms of storage as we only have to store the values for edges.

Let's see the adjacency list representation of an undirected graph.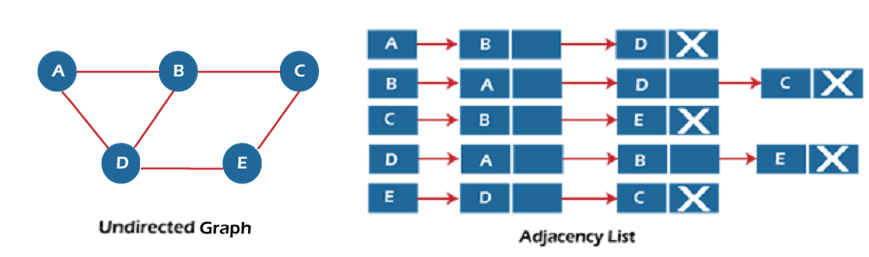

In the above figure, we can see that there is a linked list or adjacency list for every node of the graph. From vertex A, there are paths to vertex B and vertex D. These nodes are linked to nodes A in the given adjacency list.

An adjacency list is maintained for each node present in the graph, which stores the node value and a pointer to the next adjacent node to the respective node. If all the adjacent nodes are traversed, then store the NULL in the pointer field of the last node of the list.

The sum of the lengths of adjacency lists is equal to twice the number of edges present in an undirected graph.

Now, consider the directed graph, and let's see the adjacency list representation of that graph.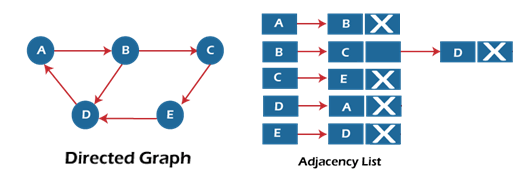

For a directed graph, the sum of the lengths of adjacency lists is equal to the number of edges present in the graph.

Now, consider the weighted directed graph, and let's see the adjacency list representation of that graph.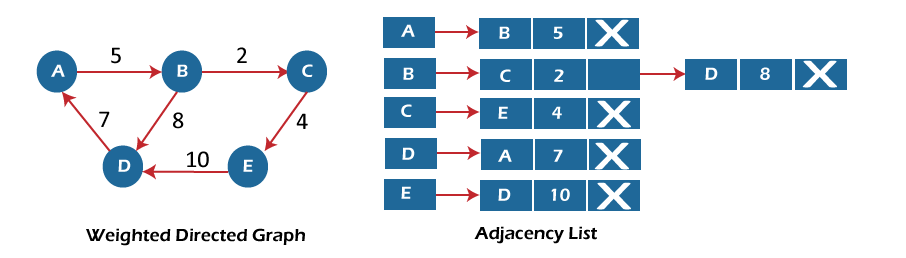

In the case of a weighted directed graph, each node contains an extra field that is called the weight of the node.

In an adjacency list, it is easy to add a vertex. Because of using the linked list, it also saves space.

Implementation of adjacency matrix representation of Graph

Now, let's see the implementation of adjacency matrix representation of graph in C.

In this program, there is an adjacency matrix representation of an undirected graph. It means that if there is an edge exists from vertex A to vertex B, there will also an edge exists from vertex B to vertex A.

Here, there are four vertices and five edges in the graph that are non-directed.

/* Adjacency Matrix representation of an undirected graph in C */

#include <stdio.h>
#define V 4 /* number of vertices in the graph */

/* function to initialize the matrix to zero */
void init(int arr[][V]) {
  int i, j;
  for (i = 0; i < V; i++)
    for (j = 0; j < V; j++)
      arr[i][j] = 0;
}

/* function to add edges to the graph */
void insertEdge(int arr[][V], int i, int j) {
  arr[i][j] = 1;
  arr[j][i] = 1;
}

/* function to print the matrix elements */
void printAdjMatrix(int arr[][V]) {
  int i, j;
  for (i = 0; i < V; i++) {
    printf("%d: ", i);
    for (j = 0; j < V; j++) {
      printf("%d ", arr[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int adjMatrix[V][V];

  init(adjMatrix);
  insertEdge(adjMatrix, 0, 1);
  insertEdge(adjMatrix, 0, 2);
  insertEdge(adjMatrix, 1, 2);
  insertEdge(adjMatrix, 2, 0);
  insertEdge(adjMatrix, 2, 3);

  printAdjMatrix(adjMatrix);

  return 0;
}

Output:

After the execution of the above code, the output will be -

Implementation of adjacency list representation of Graph

Now, let's see the implementation of adjacency list representation of graph in C.

In this program, there is an adjacency list representation of an undirected graph. It means that if there is an edge exists from vertex A to vertex B, there will also an edge exists from vertex B to vertex A.

/* Adjacency list representation of a graph in C */
#include <stdio.h>
#include <stdlib.h>

/* structure to represent a node of adjacency list */
struct AdjNode {
	int dest;
	struct AdjNode* next;
};

/* structure to represent an adjacency list */
struct AdjList {
	struct AdjNode* head;
};

/* structure to represent the graph */ 
struct Graph {
	int V; /*number of vertices in the graph*/
	struct AdjList* array;
};


struct AdjNode* newAdjNode(int dest)
{
	struct AdjNode* newNode = (struct AdjNode*)malloc(sizeof(struct AdjNode));
	newNode->dest = dest;
	newNode->next = NULL;
	return newNode;
}

struct Graph* createGraph(int V)
{
	struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
	graph->V = V;
	graph->array = (struct AdjList*)malloc(V * sizeof(struct AdjList));

	/* Initialize each adjacency list as empty by making head as NULL */
	int i;
	for (i = 0; i < V; ++i)
		graph->array[i].head = NULL;
	return graph;
}

/* function to add an edge to an undirected graph */
void addEdge(struct Graph* graph, int src, int dest)
{
	/* Add an edge from src to dest. The node is added at the beginning */
	struct AdjNode* check = NULL;
	struct AdjNode* newNode = newAdjNode(dest);

	if (graph->array[src].head == NULL) {
		newNode->next = graph->array[src].head;
		graph->array[src].head = newNode;
	}
	else {

		check = graph->array[src].head;
		while (check->next != NULL) {
			check = check->next;
		}
		// graph->array[src].head = newNode;
		check->next = newNode;
	}

	/* Since graph is undirected, add an edge from dest to src also */
	newNode = newAdjNode(src);
	if (graph->array[dest].head == NULL) {
		newNode->next = graph->array[dest].head;
		graph->array[dest].head = newNode;
	}
	else {
		check = graph->array[dest].head;
		while (check->next != NULL) {
			check = check->next;
		}
		check->next = newNode;
	}
}
/* function to print the adjacency list representation of graph*/
void print(struct Graph* graph)
{
	int v;
	for (v = 0; v < graph->V; ++v) {
		struct AdjNode* pCrawl = graph->array[v].head;
		printf("\n The Adjacency list of vertex %d is: \n head ", v);
		while (pCrawl) {
			printf("-> %d", pCrawl->dest);
			pCrawl = pCrawl->next;
		}
		printf("\n");
	}
}

int main()
{

	int V = 4;
	struct Graph* g = createGraph(V);
	addEdge(g, 0, 1);
	addEdge(g, 0, 3);
	addEdge(g, 1, 2);
	addEdge(g, 1, 3);
	addEdge(g, 2, 4);
	addEdge(g, 2, 3);
	addEdge(g, 3, 4);
	print(g);
	return 0;
}

Output:

In the output, we will see the adjacency list representation of all the vertices of the graph. After the execution of the above code, the output will be -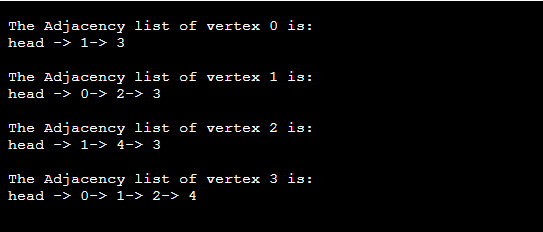

Conclusion

Here, we have seen the description of graph representation using the adjacency matrix and adjacency list. We have also seen their implementations in C programming language.

So, that's all about the article. Hope, it will be helpful and informative to you.

Next TopicBFS Algorithm

← prev next →