Introduction to Monotonic Stacks

The stack is a fundamental data structure used extensively in programming and algorithms. It operates last-in-first-out (LIFO), allowing push and pop operations but not direct access to elements in the middle. The monotonic stack is a variant of the standard stack with an additional invariant - the elements must be in strictly increasing or decreasing order. Unlike normal stacks, pushing an element may require rearranging the existing elements to maintain monotonic order. Monotonic stacks enable efficient O(n) solutions to problems involving finding the next greater or smaller element for each element in a sequence. This article introduces monotonic stacks in Python, including the motivation, implementation, time complexity analysis, and applications to problems such as the next greater element and the largest rectangle in a histogram. We will look at increasing and decreasing monotonic stacks and how maintaining the monotonic invariant speeds up certain algorithms.

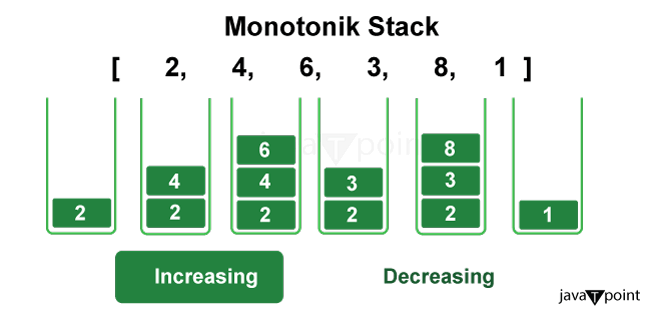
What is a Monotonic Stack?

A monotonic stack is a variant of the regular stack data structure with the additional constraint that the elements must be in strictly increasing or decreasing order.

When pushing a new element onto a monotonic stack, it is compared with the existing element on top and is only pushed after popping off any existing elements that violate the monotonic order. For example, smaller elements are popped off in an increasing monotonic stack before pushing the new element.

This ensures the newer element is always greater (or smaller) than the existing elements in the stack for increasing (or decreasing) monotonic stacks.

Maintaining this monotonic invariant allows efficient O(n) solutions to problems like:

• Next Greater Element - Find the next larger element for each element
• Previous Smaller Element - Find the previous smaller element
• Stock Span - Number of days an element is greater than the previous days
• Largest Rectangle in Histogram - Max area rectangle in histogram of bars

By contrast, these problems require O(n^2) comparisons between each element without a monotonic stack.

The monotonic stack allows tracking of "relevant" elements to compute answers for these problems in an optimal O(n) time. It is thus a powerful concept for some optimization and algorithm problems.

Properties of Monotonic Stack

• Sorted order - The defining invariant of the monotonic stack is that elements are sorted in ascending or descending order from bottom to top. Smaller/larger elements are popped to maintain the order when pushing a new element.
• LIFO operations - Being a variant of stacks, the monotonic stack only allows push and pop operations. Elements can only be inserted/removed from the top of the stack in a LIFO manner. No other access is provided.
• Single-sort direction - A monotonic stack maintains a single-sort direction - either increasing or decreasing. It cannot keep elements in both ascending and descending order simultaneously. The direction depends on the use case.
• Non-distinct elements - Unlike typical sorted data structures, a monotonic stack allows duplicate element values. However, their relative order is still maintained based on the insertion order.
• Amortized O(1) ops - Individual push/pop may take O(n) time if many elements are popped, but over a sequence of ops, it takes O(1) amortized time. Similar to dynamic arrays.
• Space efficiency - Monotonic stack is space efficient, requiring only O(n) space in addition to the input array of size n. Much less than a sorted array.
• Online processing - It can incrementally process elements in a stream without looking at future elements. Useful for online algorithms.
• Resets relations - A new maximum or minimum resets the relevant comparisons and relations from then on. Does not retain full history.
• No random access - Direct random access is not supported. Only sequential LIFO-based push/pop access.
• Generic data - Can work with any data types that can be compared, like numbers, strings, etc. Not restricted to only numbers.

Difference between Monotonic Stacks and Normal Stacks

The key differences between normal stacks and monotonic stacks are:

• Ordering - Normal stacks have no ordering of elements. Monotonic stacks maintain ascending or descending order.
• Push operation - In normal stacks, push is always O(1). In monotonic stacks, push can be O(n) in the worst case if elements are popped to maintain order, but is O(1) amortized over a sequence of operations.
• Pop operation is O(1) for normal and monotonic stacks.
• Peek operation - Peek is O(1) for both. Returns top element.
• Element access - Normal stacks allow random access to any element. Monotonic stacks only allow sequential push/pop access in LIFO order.
• Applications - Normal stacks are used for reversing orders, tracking states, etc. Monotonic stacks are used to find previous/next significant elements in sequences.
• Space complexity - Both require O(n) extra space for a sequence of n elements.
• Implementation - Monotonic stacks need just a few additional lines of code to check/maintain order while pushing.

So, in summary, monotonic stacks differ only in maintaining a sort order while having similar LIFO access. This ordering allows efficient algorithms to find relatively greater/smaller elements in sequences.

Advantages of Monotonic Stacks

• Optimal time complexity - Problems like the next greater/smaller element, stock span, etc., can be solved in O(n) time using a naive approach with a monotonic stack versus O(n^2). Maintaining the sort order allows tracking useful elements to calculate answers.
• Space efficient - Monotonic stack only requires O(n) extra space and the input array. No additional data structure is needed.
• Easy to implement - A monotonic stack can be implemented easily by modifying a few lines of code for a regular stack to check/maintain sort order while pushing.
• Versatile - Both increasing and decreasing variants allow for solving different problems. Increasing order is useful when looking ahead and decreasing when looking behind.
• Relevant elements only - The monotonic stack only keeps elements useful for finding a solution at any point; the rest are popped off. It saves space and calculations over keeping a full window.
• No full sorts/scans - Unlike some solutions, full sorting or scanning of the array is unnecessary. Pushing/popping takes care of ordering.
• Cache-friendly - Access to elements is sequential instead of random access in some other structures. Better use of CPU caches.
• Easy to reason - The monotonic variant makes logic/flow easy to understand and reason about during implementations.

Overall, the monotonicity invariant allows very efficient algorithms rivalling some advanced data structures while being simple enough to code quickly. An elegant and powerful concept!

Different Applications of Monotonic Stacks

• Next Greater Element - Find the next larger element for each element in an array. Increasing the monotonic stack gives an O(n) solution. Useful in problems involving finding greater elements.
• Previous Smaller Element - Find the previous smaller element for each element in O(n) time using a decreasing monotonic stack. Applications in financial analysis.
• Stock Span Problem - Calculate the span for each day - the number of consecutive days with higher prices. A monotonic stack gives the optimal solution.
• Largest Rectangle in Histogram - Find the largest rectangle area possible from the heights of contiguous bars. O(n) solution using decreasing monotonic stack.
• Evaluate Expressions - Monotonic stack can evaluate expressions with minimum operations required. Used in calculator algorithms.
• Nearest Smaller Values - Find the nearest smaller value on the left and right of each array element. Monotonic stacks can do this in linear time.
• Rainwater Trapping - Calculate the total trapped water between the heights of the bars. Solved efficiently using two monotonic stacks.
• Longest Increasing Subsequence - Monotonic stack helps reconstruct the longest increasing subsequence ending at each index.
• Nearest Greater Values - Find the nearest greater elements on each element's left and right sides in linear time.

So, in summary, monotonic stacks shine in problems involving efficiently finding previous or next significant elements in sequences. The ordered structure allows tracking useful elements to calculate answers in optimal time.

Increasing Monotonic Stack

An increasing monotonic stack maintains elements in strictly ascending order from bottom to top. The key properties are:

• The new element pushed is always greater than the existing elements. Smaller elements are popped to maintain order.
• Follows last-in-first-out (LIFO) order for access via push/pop.
• In the worst case, push takes s O(n) time if many pops are n needed, but O(1) amortized over sequence.
• Finding the next larger element for each element takes O(n) time.
• Useful when looking ahead in sequence for greater elements.
• Applications include the next greater element, stock span, evaluating expressions, etc.

Pushing pseudocode:

Decreasing Monotonic Stack

A decreasing monotonic stack maintains elements in strictly descending order from bottom to top. The key properties are:

• The new element pushed is always smaller than the existing elements. Larger elements are popped.
• It also follows the last-in-first-out (LIFO) order of access.
• Push takes O(n) worst-case time, but O(1) amortized over ops.
• Finding the previous smaller element takes O(n) time.
• Useful when looking behind in sequence for smaller elements.
• Applications include previous smaller elements, the largest rectangle in the histogram, etc.

Pushing pseudocode:

In summary, increasing monotonic stacks look ahead and decreasing stacks look behind. Both provide efficient O(n) solutions for their problems by dynamically maintaining sorted order.

Python Implementation

Strictly Increasing Monotonic Stacks

1. Create a MonotonicStack class to represent the stack. Have an empty list of 'items' to store the elements.
2. Define the isEmpty() method to check if the stack is empty. Simply check if the items list is empty by comparing to [].
3. Define the peek() method to return the top element. Return the last element in the items list using index len(items)-1.
4. Define the push(x) method to push new element x by:
5. a) Loop while the stack is not empty AND the top element is less than x
6. b) Inside the loop, pop elements by calling the custom pop() method
7. c) After the loop, append x to the items list
8. Define a pop() method to pop top element:
9. a) Check that the stack is not empty
10. b) Remove the last element from the items list using del on index len(items)-1
11. Define the printStack() method to print the items list for debugging.
12. The key steps are checking the order in push() and removing the last element in pop().
13. Together, these maintain the increasing order when elements are pushed or popped.
14. No Python list methods like append() or pop() are used.

This algorithm manually enforces the monotonic order by iterating and comparing elements before pushing. The pop just removes the last element.

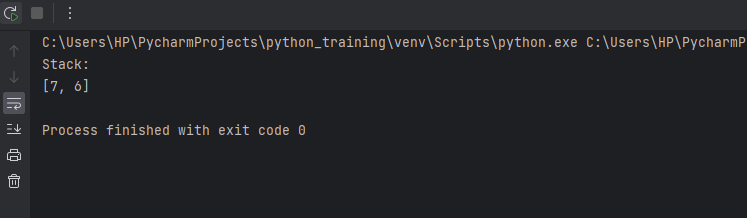
Output:

Strictly Decreasing Monotonic Stacks

1. Create MonotonicStack class to represent stack with empty items list
2. Define the isEmpty() method to check if the stack is empty. Compare items to []
3. Define peek() to return the top element. Return the last element in the items list using an index.
4. Define the push(x) method to push new element x:
5. a) Loop while stack not empty AND top element is greater than x
6. b) Inside the loop, pop elements by calling the custom pop() method
7. c) After the loop, append x to the items list
8. Define the pop() method to remove the top element:
9. a) Check that the stack is not empty
10. b) Remove the last element from items using the index
11. Define printStack() to print items list
12. The key steps are:
13. a) Checking order in push() by comparing to top
14. b) Popping larger elements before appending x
15. c) Removing the last element in pop()
16. These steps enforce the decreasing order while pushing and popping.
17. No Python list methods like append()/pop() are used.
18. Order is maintained by iterating and comparing elements before append.

By modifying the order check-in push(), we can implement a decreasing monotonic stack without predefined functions.

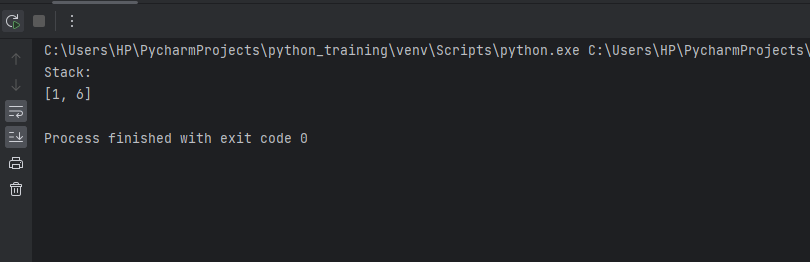
Output: