Queue for Competitive Programming
Introduction
Coders who enjoy a fast-paced, competitive setting can demonstrate their problem-solving skills in competitive programming, an exciting arena. In order to effectively traverse the complexities of algorithmic problems, one needs to make use of the capabilities of multiple data structures, with the simple queue standing tall among them. A basic data structure that adheres to the First-In-First-Out (FIFO) principle is a queue. Imagine it as a queue of people waiting to receive a service; the first person in line gets served first. Queues are very useful in competitive programming because they are straightforward, simple to implement, and effective in a wide range of scenarios.
Breadth-First Search (BFS)
In competitive programming, one of the most common uses of queues is in the context of graph algorithms, specifically in Breadth-First Search (BFS). BFS examines a graph level by level, and it does so elegantly with the help of a queue. A sample of C code that illustrates how BFS is implemented with a queue is provided below:
Code
Output:
Code Explanation
Input
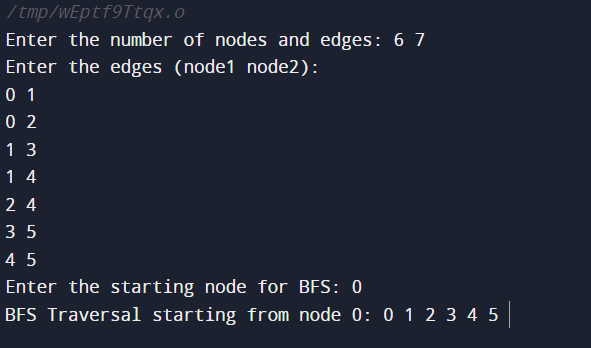
- The number of nodes and edges in the graph is entered into the program.
- After that, assuming an undirected graph, it accepts input for each edge.
BFS Function
- The BFS traversal is executed by the bfs function, commencing at a specified node.
- During traversal, it enqueues and dequeues nodes using a queue (queue).
- To prevent revisiting, the visited array maintains track of the nodes that have been visited.
Main Function
- Based on user input, the main function initializes the graph.
- The user is prompted to enter the BFS startup node.
- Lastly, it prints the BFS traversal beginning at the designated node after invoking the bfs function.
Simulation Problems
Task scheduling and event processing are two examples of real-world scenarios that are frequently simulated in competitive programming. Because they are naturally intuitive, queues work well in these kinds of simulations. Take a look at this little bit of C code for a basic task-scheduling simulation:
Code
Output:
Code Explanation
Task Structure
- To represent each task, the code defines a structure called struct Task.
- Task identifier (id) and duration (the amount of time needed to finish the task) are the two components of every task.
Task Array
- Instances of the struct Task are declared in an array called tasks.
- MAX_TASKS sets the maximum size of the array.
Function of the Task Scheduler (scheduleTasks)
- The number of tasks, denoted by the integer n, is a parameter passed to the function.
- To enqueue tasks, it makes use of a queue, which is implemented as an array named queue.
- According to their array index, tasks are enqueued in the order that they are received.
Task Queuing
- The tasks are iterated through in a loop, and the index of each task is added to the queue.
Processing Tasks
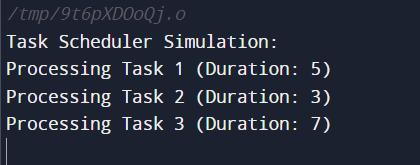
- The function then executes tasks in the order that they were queued inside a while loop.
- The task that will be processed next is indicated by the front of the queue being dequeued.
- The console receives a printout of the processed task's ID and duration.
Main Function
- A few tasks are initialized for demonstration in the main function.
- To simulate task scheduling, the number of initialized tasks is passed to the scheduleTasks function.
Results
- The order in which tasks are completed and their corresponding durations are shown in the program's output.
Sliding Window Problems
When analyzing a subarray or subsequence of a fixed size, as in sliding window problems, queues prove to be an effective tool. The following sample of C code illustrates how to use a sliding window method to find the maximum element in a subarray:
Code
Output:

Code Explanation
- Function: slidingWindowMax
Parameters
- arr: the input array
- n: The array's dimensions.
- k: The sliding window's size.
- The function sets up a queue to hold the array's element indices.
- To initialize the queue, it processes the first k elements independently, eliminating elements from the back that are smaller than the current element.
- After processing the remaining elements, the maximum element for each window is printed, and the queue is updated appropriately.
Main Function
- {1, 3, -1, -3, 5, 3, 6, 7} are the elements of an array arr that are given.
- There is a window size of 3.
Implementation
- The slidingWindowMax function is used to determine the maximum elements in subarrays of size k, and the program prints the input array.
- The maximum elements for every window are shown in the output as the window moves through the input array.
Dynamic Connectivity Problems
Managing a collection of elements that are periodically connected or disconnected is the focus of dynamic connectivity problems. The Union-Find (Disjoint Set Union) data structure is a traditional data structure that is used to address these kinds of issues. It can efficiently handle finding the representative (find) and merging (union) of disjoint sets. The Union-Find data structure is implemented simply in C below to address a dynamic connectivity issue:
Code
Output:
Code Explanation
Initialization
- By initializing the parent array, the initialize function configures the Union-Find data structure. The parent array is used to preserve the structure of disjoint sets, where each element is initially its own set.
Find Operation (with Compression of Path)
- Finding the root (representative) of the set to which a given element belongs is the responsibility of the find function. It updates the parent pointers along the path to the root during a find operation because it uses path compression. This aids in the optimization of find operations that follow.
Merge Operation (Union by Rank)
- By making the root of one set the parent of the root of the other, the merge function joins two sets. A simple union-by-rank heuristic is used to optimize the merging process and preserve a balanced tree structure.
Display Sets
- Each element's index and current representative (root) are printed by the displaySets function. This makes it possible to see the sets.
Main Function
- The number of elements (n) in the main function is set to 6.
- The initialize function is used to create initial singleton sets for each element in the Union-Find data structure.
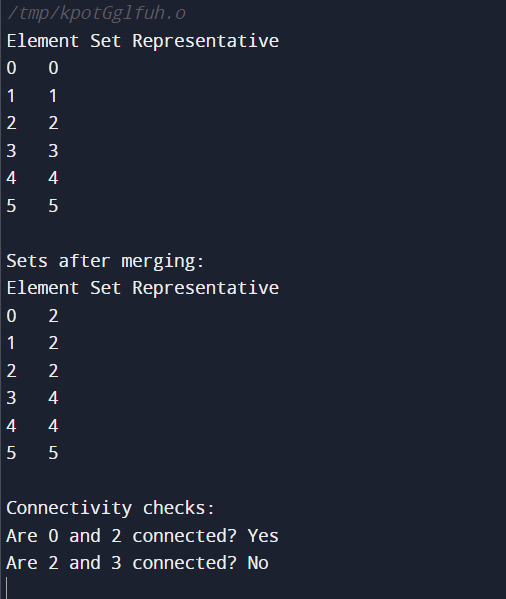
- Using the displaySets function, the sets are shown before any merging operations.
- Elements 0 through 2 are combined, along with elements 3 and 4, to replicate how elements connect in dynamic scenarios.
- Once the sets are merged, they are shown once more.
- The find function is used to perform connectivity checks and determine whether or not specific elements are connected.
Output
- The output displays the initial sets (singleton sets), in which every element is in a separate set.
- The sets are updated, reflecting the connections made following merging operations.
- Connectivity checks make sure that certain elements belong in different sets (not connected) or the same set (connected).
|




 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









