Find kth Smallest Element in a Binary Search Tree

A binary search tree is a hierarchical data structure where each node comprises two child nodes which in turn satisfies the property that the value of every node in the left subtree is supposed to be less than the parent node and that the value in the right subtree should be greater than the parent node. As the kth smallest element refers to an element that, when visiting a binary tree in an in-order traversal pattern, we have to stop, wait, and search for the kth element in the tree and return the result.

Some advantages are: -

Efficient search- binary search trees are known for their vigorous report in search operations, and the smallest element is no exception.
Sorted order- the kth smallest element operation represents the elements in a kth smallest sorted order, which is very helpful, especially when looking for the elements to be presented in an organized manner.

In this article, we are going to see and find out the kth smallest element in a binary search tree. Suppose we are given a binary tree and K as an input, and we must find out the smallest element. This article will show the code solution to the following problem.

Implementation

// Creating a basic C++ in-order traversal program to help us discover the kth smallest element in a binary search tree. 
#include <iostream>

using namespace std;

// creating a new binary search tree node
struct __nod {
	int record;
	__nod *Lft, *Rt;
	__nod(int x)
	{
		record = x;
		Lft = Rt = NILL;
	}
};

// Creating a recursive function to help us insert a new key into the BST.
__nod* insert(__nod* root, int x)
{
	if (root == NILL)
		return new __nod(x);
	if (x < root->record)
		root->Lft = insert(root->Lft, x);
	else if (x > root->record)
		root->Rt = insert(root->Rt, x);
	return root;
}

// Creating a function to help us discover the kth smallest element in the binary search tree. 
// The count here signifies the total no. of nodes processed so far.
int count = 0;
__nod* kthSmallest(__nod* root, int& k)
{
	// Writing the basic case
	if (root == NILL)
		return NILL;

	// Now, we have to search in the left subtree
	__nod* Lft = kthSmallest(root->Lft, k);

	//If the element is found in the left subtree, we must return it.
	if (Lft != NILL)
		return Lft;

	//If the current element is the smallest, we must return that. 
	count++;
	if (count == k)
		return root;

	// Or else, we have to go back and search in the right subtree
	return kthSmallest(root->Rt, k);
}

// Creating a function to print the kth smallest element in the BST. 
void printKthSmallest(__nod* root, int k)
{
	// We must maintain an index to check the number of nodes processed.
	__nod* res = kthSmallest(root, k);
	if (res == NILL)
		cout << "There are less than k __nods in the BST";
	else
		cout << "K-th Smallest Element is " << res->record;
}

//Writing the main function to test the above functions
int main()
{
	__nod* root = NILL;
	int kys[] = { 20, 8, 22, 4, 12, 10, 14 };

	for (int x : kys)
		root = insert(root, x);

	int k = 3;
	printKthSmallest(root, k);
	return 0;
}

Output

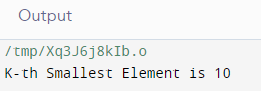
Find kth Smallest Element in a Binary Search Tree

A step-by-step explanation of the code

The code begins by including the necessary header files for the program's various input and output operations.
Next, we define a structure 'Node' to represent a node in the binary search tree, and it has the following three members: a data value and a pointer to the left and right child.
Then we create an insert function to insert a new key to the BST. It takes two parameters: a root value and the value that should be inserted.
The 'count' variable is declared outside any function and is subjected to 0.
Now, we move to the central part and create the 'KthSmallest' function, a recursive function used to find out the Kth smallest element in the binary tree and holds the main logic of the program.
Next, the 'printKthSmallest' function is used to print the result, take the value of k as parameters, and display the results.
The main function is the entry point of the program. A binary tree is created in it, and the root of the BST is initialized to NULL.
Using a loop, we can take each value from the key and move it to the binary tree using the insert function.
The 'printKthSmallest' function is called with the root of the BST to display the result.
Finally, the main program returns 0, indicating the successful execution of the program.

Example 2)

// Creating a basic C++ in-order traversal program to help us discover the kth smallest element in a binary search tree. 
#include <stdlib.h>

// creating a new binary search tree node
typedef struct __nod {
	int record;
	struct __nod *Lft, *Rt;
} __nod;

struct __nod* new___nod(int x)
{
	struct __nod* p = malloc(sizeof(struct __nod));
	p->record = x;
	p->Lft = NILL;
	p->Rt = NILL;
	return p;
}
// Creating a recursive function to help us insert a new key into the BST.
__nod* insert(__nod* root, int x)
{
	if (root == NILL)
		return new___nod(x);
	if (x < root->record)
		root->Lft = insert(root->Lft, x);
	else if (x > root->record)
		root->Rt = insert(root->Rt, x);
	return root;
}
// Creating a function to help us discover the kth smallest element in the binary search tree. 
// The count here signifies the total no. of nodes processed so far.
int count = 0;
__nod* kthSmallest(__nod* root, int k)
{
	// Writing the basic case
	if (root == NILL)
		return NILL;
	// Now, we have to search in the left subtree
	__nod* Lft = kthSmallest(root->Lft, k);
	//If the element is found in the left subtree, we must return it.
	if (Lft != NILL)
		return Lft;
	//If the current element is the smallest, we must also return that. 
	count++;
	if (count == k)
		return root;
	// Or else, we have to go back and search in the right subtree
	return kthSmallest(root->Rt, k);
}

// Creating a function to print the kth smallest element in the BST. 
void printKthSmallest(__nod* root, int k)
{
	// We must maintain an index to check the number of nodes processed.
	__nod* res = kthSmallest(root, k);
	if (res == NILL)
		printf("There are less than k __nods in the BST");
	else
		printf("K-th Smallest Element is %d", res->record);
}

//Writing the main function to test the above functions 
int main()
{
	__nod* root = NILL;
	int kys[] = { 20, 8, 22, 4, 12, 10, 14 };
	int kys_size = sizeof(keys) / sizeof(kys[0]);

	for (int i = 0; i < kys_size; i++)
		root = insert(root, kys[i]);

	int k = 3;
	printKthSmallest(root, k);
	return 0;
}

Output

A step-by-step explanation of the code

The code begins by including the necessary header files for the program's various input and output operations.
Next, we define a structure 'Node' to represent a node in the binary search tree, and it has the following three members: a data value and a pointer to the left and right child.
Then we create an insert function to insert a new key to the BST. It takes two parameters: a root value and the value that should be inserted.
The 'count' variable is declared outside any function and is subjected to 0.
Now, we move to the central part and create the 'KthSmallest' function, a recursive function used to find out the Kth smallest element in the binary tree and holds the main logic of the program.
Next, the 'printKthSmallest' function is used to print the result, take the value of k as parameters, and display the results.
The primary function is the entry point of the program. A binary tree is created in it, and the root of the BST is initialized to NULL.
Using a loop, we can take each value from the key and move it to the binary tree using the insert function.
The 'printKthSmallest' function is called with the root of the BST to display the result.
Finally, the main program returns 0, indicating the successful execution of the program.

Example 3)

// Creating a basic Java in-order traversal program to help us discover the kth smallest element in a binary search tree. 
import java.io.*;
// creating a new binary search tree node
class __nod {
	int record;
	__nod Lft, Rt;
	__nod(int x)
	{
		record = x;
		Lft = Rt = NILL;
	}
}

class TPT {

	static int count = 0;
// Creating a recursive function to help us insert a new key into the BST.
	public static __nod insert(__nod root, int x)
	{
		if (root == NILL)
			return new __nod(x);
		if (x < root.record)
			root.Lft = insert(root.Lft, x);
		else if (x > root.record)
			root.Rt = insert(root.Rt, x);
		return root;
	}
// Creating a function to help us discover the kth smallest element in the binary search tree. 
// The count here signifies the total no. of nodes processed so far.
	public static __nod kthSmallest(__nod root, int k)
	{
	// Writing the basic case
		if (root == NILL)
			return NILL;
	// Now, we have to search in the left subtree
		__nod Lft = kthSmallest(root.Lft, k);
	//If the element is found in the left subtree, we must return it.
		if (Lft != NILL)
			return Lft;
	//If the current element is the smallest, we must also return that. 
		count++;
		if (count == k)
			return root;
	// Or else, we have to go back and search in the right subtree
		return kthSmallest(root.Rt, k);
	}

// Creating a function to print the kth smallest element in the BST. 
	public static void printKthSmallest(__nod root, int k)
	{
		__nod res = kthSmallest(root, k);
		if (res == NILL)
			System.out.println("There are less than k __nods in the BST");
		else
			System.out.println("K-th Smallest Element is " + res.record);
	}

	public static void main(String[] args)
	{
		__nod root = NILL;
		int kys[] = { 20, 8, 22, 4, 12, 10, 14 };
		for (int x : kys)
			root = insert(root, x);
		int k = 3;
		printKthSmallest(root, k);
	}
}

Output

A step-by-step explanation of the code

The code begins by including the 'java.io' package.
Next, we define a structure 'Node' to represent a node in the binary search tree, and it has the following three members: a data value and a pointer to the left and right child.
We define a nested class called 'TPT' that contains the logic of the program.
Then we create an insert function to insert a new key to the BST. It takes two parameters: a root value and the value that should be inserted.
The 'count' variable is declared outside any function and is subjected to 0.
Now, we move to the central part and create the 'KthSmallest' function, a recursive function used to find out the Kth smallest element in the binary tree and holds the main logic of the program.
Next, the 'printKthSmallest' function is used to print the result, take the value of k as parameters, and display the results.
The primary function is the entry point of the program. A binary tree is created in it, and the root of the BST is initialized to NULL.
Using a loop, we can take each value from the key and move it to the binary tree using the insert function.
The 'printKthSmallest' function is called with the root of the BST to display the result.
Finally, the main program returns 0, indicating the successful execution of the program.