Time Complexity of building a heap

The time complexity of building a heap using the heapify operation depends on the method we are using; let us know what the methods we have are:

There are two standard methods for building a heap:

Naive Approach (Insertion):

In this approach, we must insert each element into the Heap individually.

Starting with an empty heap, we insert elements one by one.

Since you insert n elements, the overall time complexity of building the Heap using this approach is O(n log n).

Floyd's Algorithm (Heapify):

Floyd's algorithm is a more efficient method for building a heap.

It works in a bottom-up manner, starting from the last non-leaf node and heapifying each node.

The time complexity of heapifying a single node is O(log n), where n is the number of elements in the Heap.

Since there are n/2 non-leaf nodes in a heap, the overall time complexity of building the Heap using Floyd's algorithm is O(n).

In practice, Floyd's algorithm is preferred for building heaps due to its better time complexity, making it more efficient than the naive insertion approach. The constant factors involved in the O(n) term for Floyd's algorithm are typically smaller than the constant factors in the O(n log n) term for the insertion approach.

Let us implement the code for both the approaches:

Let us implement the code for the naïve approach:

CODE:

#includ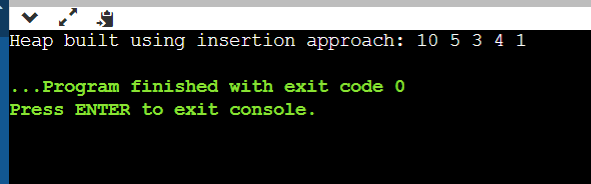e <iostream>
#include <vector>
void heapify(std::vector<int>& heap, int index) {
    int parent = (index - 1) / 2;
    while (index > 0 && heap[index] > heap[parent]) {
        std::swap(heap[index], heap[parent]);
        index = parent;
        parent = (index - 1) / 2;
    }
}
void buildHeapInsertion(std::vector<int>& arr) {
    for (int i = 1; i < arr.size(); ++i) {
        heapify(arr, i);
    }
}
int main() {
    std::vector<int> arr = {4, 10, 3, 5, 1};
    buildHeapInsertion(arr);
    std::cout << "Heap built using insertion approach: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    return 0;
}

Output:

Explanation:

heapify function:

Takes a heap and an index as parameters. Moves the element at the given index up the Heap until the heap property is satisfied.

buildHeapInsertion function:

It Iterates over the array starting from the second element. Calls heapify for each element, effectively inserting it into the Heap.

main function:

It Initializes an array with values. Calls buildHeapInsertion to build the Heap using the insertion approach. Prints the resulting Heap.

Time Complexity:

The time complexity of the provided heap construction using the insertion approach is O(n log n), where n is the number of elements in the array.

Another Approach: Heapify:

#includ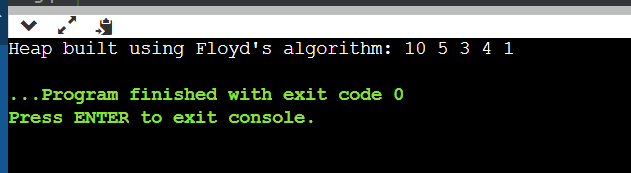e <iostream>
#include <vector>
void heapify(std::vector<int>& heap, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    if (left < n && heap[left] > heap[largest]) {
        largest = left;
    }
    if (right < n && heap[right] > heap[largest]) {
        largest = right;
    }
    if (largest != i) {
        std::swap(heap[i], heap[largest]);
        heapify(heap, n, largest);
    }
}
void buildHeapFloyd(std::vector<int>& arr) {
    int n = arr.size();

    for (int i = n / 2 - 1; i >= 0; --i) {
        heapify(arr, n, i);
    }
}
int main() {
    std::vector<int> arr = {4, 10, 3, 5, 1};
     buildHeapFloyd(arr);
    std::cout << "Heap built using Floyd's algorithm: ";
    for (int num : arr) {
        std::cout << num << " ";
    }
    return 0;
}

Output:

Explanation:

heapify function:

Takes a heap, the size of the Heap (n), and an index as parameters.

Compares the element at the given index with its left and right children and swaps with the largest if needed.

Recursively calls heapify on the swapped child index.

buildHeapFloyd function: Iterates from the last non-leaf node to the root of the Heap.

Calls heapify for each node, effectively transforming the array into a heap.

main function:

Initializes an array with values.

Calls buildHeapFloyd to build the Heap using Floyd's algorithm. Prints the resulting Heap.

Time Complexity:

The time complexity of the provided heap construction using Floyd's algorithm (also known as heapify or bottom-up heap construction) is O(n), where n is the number of elements in the array.

Both approaches result in a valid heap at the end. The first approach (naive insertion) inserts elements one by one into the Heap, while the second approach (Floyd's algorithm) uses a bottom-up approach to build the Heap efficiently.

Next TopicBuild linear type suffix

← prev next →