Polish and Reverse Polish Notation
Introduction
Before starting the discussion about the Polish and Reverse Polish Notation, we must understand the reason that why do we need to write these two expressions.
Types of Notations
There are three types of polish notations that exist in the data structure:
- Infix Notation
- Prefix Notation
- Postfix Notation
The common expression used in mathematics is the infix notation which faces difficulties when evaluation is done by a computer.
- In infix notation, each operator is written between the operands. For example: P * Q + R * S is an arithmetical expression written in infix notation, here * denotes multiplication. In this expression P and Q are two operands and * is an operator, similarly R and S are the two operands and * is an operator.
The order of precedence of different operators is as follows:
- Exponents have precedence one.
- Multiplication and Division has precedence two.
- Addition and subtraction have precedence three.
Form this example we see that while evaluating arithmetic expressions in infix notation it is necessary to scan the expression from both ends. And this is a difficult task for computer to evaluate the expression written in infix notation. So, to overcome this problem The Polish mathematician "Lukasiewicz" suggested that arithmetic expressions can be written in prefix notation and this notation is referred as polish notation.
Polish Notation
Polish notation also called as Prefix notation is a method or a way that shows expressions in a different arithmetic expression form. Prefix Notation means that operations are written before the operands.
This notation was devised by Polish mathematician Lukasiewicz. An arithmetic expression mainly comprises of 2 parts, that are Operands and Operators.
- Operands are either numbers or variables that can be replaced by numbers to evaluate the expressions.
- Operators are symbols symbolizing the operation to be performed between operands present in the expression.
Generally, humans find infix polish notation much easier to understand than postfix or reverse polish notation. Converting each expression from infix to postfix. Each operator has its priority for an expression. For example, if we take some operators, i.e., +, -, *, /, then these will be arranged in priority.
- Higher Priority Operators: *, /, %
- Lower Priority Operators:+, -
- Order of Operators:+, -, ∗, /, ^
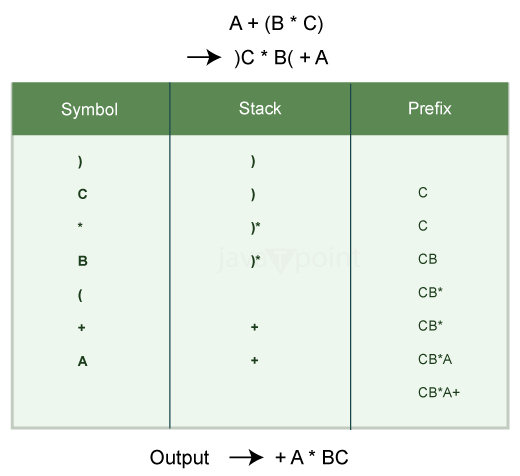
Conversion of an Infix Expression to Prefix Expression
Algorithm:
- Add ")" to the end of the given expression's infix polish notation and push "(" into the stack.
- Reverse the whole expression from backwards to forward in sequence.
- Then follow the following steps given below accordingly:
- Place the element onto the stack if "(" is found. We add an operand-that is, a variable or a number-into the prefix or polish notation whenever we come across one.
- In the event that ")" is encountered, we add these elements to the prefix expression by popping elements from the stack until "(" is the popped element. Subsequently, remove "(" from the stack and refrain from adding it to the prefix expression.
- If an operator "*" is found, repeatedly remove it from the stack and add each operator that has the same precedence as or greater than operator "*" to the prefix expression.
- Then the final expression created in the stack is reversed in order to undo the 2nd step to get the final answer.
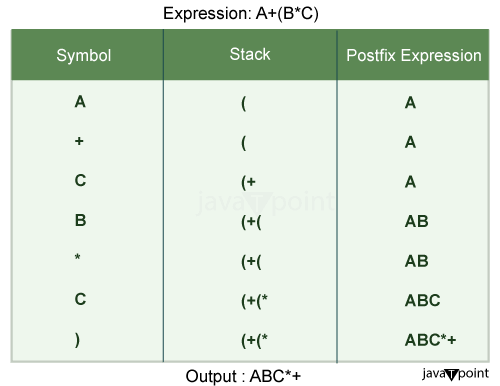
Conversion of an Infix Expression to Postfix Expression
Algorithm:
- Add ")" to the end of the given expression's infix polish notation and push "(" into the stack.
- For every element included in the Infix Polish Notation, follow the procedures listed below once more.
- Place the element onto the stack if "(" is found. We add an operand-that is, a variable or a number-into the postfix or reverse polish notation whenever we come across one.
- In the event that ")" is encountered, we add these elements to the postfix expression by popping elements from the stack until "(" is the popped element. Subsequently, remove "(" from the stack and refrain from adding it to the postfix expression.
- If an operator "x" is found, repeatedly remove it from the stack and add each operator that has the same precedence as or greater than operator "x" to the postfix expression.
- All of the elements will be removed from the stack and added to the postfix expression once step 2 has been completed on each element.
This is the final expression of the given Notation and these algorithms are further used to solve numerical questions.
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









