K-th Largest Sum Contiguous Subarray

Introduction

Within the larger class of subarray sum problems, the K-th Largest Sum Contiguous Subarray problem is a difficult algorithmic task. The objective is to determine the K-th largest sum among an array's potential contiguous subarrays. This issue has a wide range of applications in fields where it's critical to find important patterns or trends within a dataset, such as finance, data analysis, and image processing. Gaining insight from comprehending data variations and pinpointing particular segments with the highest cumulative sums can be useful in real-world situations. Finding the K-th largest sum contiguous subarray, for example, could be used in financial data analysis to identify periods of notable financial growth or decline. Similar to this, this issue can be used in image processing to find areas with the highest pixel values, which may indicate significant features or abnormalities.

In order to solve the K-th Largest Sum Contiguous Subarray problem, effective algorithms that minimize both time and space complexity are needed to handle large datasets. Approaches ranging from brute-force methods to dynamic programming and sophisticated methods utilizing data structures such as heaps provide distinct insights into the effective identification of the K-th largest sum contiguous subarray.

Brute Force Approach

Using a brute force approach is the most direct method for solving the K-th Largest Sum Contiguous Subarray problem. This entails creating every conceivable subarray and figuring out how much each one is worth. After that, we return the K-th largest sum by sorting the sums in descending order.

Code

#include <stdio.h>
#include <stdlib.h>
int compare(const void *a, const void *b);
int kthLargestSumSubarray(int arr[], int n, int k) {
    int *allSums = (int *)malloc(sizeof(int) * n * (n + 1) / 2);
    int index = 0;
    for (int i = 0; i < n; i++) {
        int currentSum = 0;
        for (int j = i; j < n; j++) {
            currentSum += arr[j];
            allSums[index++] = currentSum;
        }
    }
    qsort(allSums, index, sizeof(int), compare);
    return allSums[k - 1];
}
int compare(const void *a, const void *b) {
    return (*(int *)b - *(int *)a);
}
int main() {
    int arr[] = {4, -8, 9, -4, 1, -8, -1, 6};
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 3;
    int result = kthLargestSumSubarray(arr, n, k);
    printf("The %d-th largest sum contiguous subarray is: %d\n", k, result);
    return 0;
}

Output:

Code Explanation

Dynamic Memory Allocation

An array (allSums) is a dynamically allocated memory to hold all possible subarray sums.

Subarray Sums with Nested Loop

To get every possible subarray sum, two nested loops iterate over the array.
The subarray's starting index is represented by the outer loop (i).
The subarray's terminating index is represented by the inner loop (j).

Method for Computing Subarray Sums

The current subarray's sum is determined using a variable called currentSum.

Sorting Subarray Sums

To sort the array of subarray sums in descending order, utilize the qsort function.
The sorting procedure uses the compare function as a comparator.

Return K-th Largest Sum

From the sorted array of subarray sums, the K-th largest sum is extracted and given back.

The Function of the Comparator (compare)

The qsort function declares that it will use a comparator function.
Two integers are compared in descending order.

Main Function

The main function calls the kthLargestSumSubarray function, initializes an array, and sets the value of K.
The console displays the outcome.

Time and Space Complexity Analysis

The sorting operation with the `qsort} function dominates the time complexity of the given code for locating the K-th largest sum contiguous subarray. O(n^2) time complexity, where 'n' is the length of the input array, is contributed by the nested loops that generate all possible subarray sums. The sorting operation, on the other hand, dominates the total time complexity; in the average case, its time complexity is O(n*log(n)). Consequently, O(n^2 + n* log (n)) is the ultimate time complexity; however, in actual use, the sorting process is likely the main influence.

Space complexity is O(n^2) because of the space needed to store all possible subarray sums, which is determined by using dynamic memory allocation for an array (allSums) whose size is proportional to the number of subarrays (n*(n+1)/2 for an array of length 'n'). Variables and the comparator function also take up a constant amount of space, which doesn't significantly affect the overall space complexity.

Dynamic Programming Approach

The maximum sum contiguous subarray can be found using the well-known dynamic programming method known as Kadane's algorithm. This algorithm can be adjusted so that, as iterating through the array, it keeps track of the K-th largest sum.

Code

int max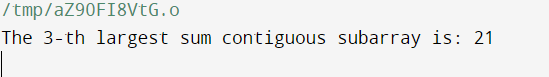(int a, int b) {
    return (a > b) ? a : b;
}
int kthLargestSumSubarray(int arr[], int n, int k) {
    int *currentSum = (int *)malloc(sizeof(int) * n);
    currentSum[0] = arr[0];
    int *kthSums = (int *)malloc(sizeof(int) * k);
    for (int i = 0; i < k; i++) {
        kthSums[i] = 0;
    }
    for (int i = 1; i < n; i++) {
        currentSum[i] = max(arr[i], currentSum[i - 1] + arr[i]);
        for (int j = k - 1; j > 0; j--) {
            kthSums[j] = max(kthSums[j], kthSums[j - 1] + currentSum[i]);
        }
        kthSums[0] = max(kthSums[0], currentSum[i]);
    }
    int result = kthSums[k - 1];
    free(currentSum);
    free(kthSums);
    return result;
}
int main() {
    int arr[] = {4, -8, 9, -4, 1, -8, -1, 6};
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 3;
    int result = kthLargestSumSubarray(arr, n, k);
    printf("The %d-th largest sum contiguous subarray is: %d\n", k, result);
    return 0;
}

Output:

Code Explanation

Maximum Function

Using the ternary operator, a straightforward function is defined to determine the maximum of two integers.

Largest Contiguous Subarray Function with K-th Order

CurrentSum and kthSums are the two arrays for which dynamic memory is allotted.
The current sum of the subarray ending at each index is stored in currentSum.
The K-th largest sums are initially stored in kthSums.
CurrentSum and kthSums are updated as the array is iterated through.
The variable result contains the K-th largest sum.
In order to stop memory leaks, dynamic memory is released.

Main Function

Sets the length of an array, its initial value, and K.
Makes use of the array, length, and K parameters to invoke the kthLargestSumSubarray function.
The outcome is printed to the console.

Time and Space Complexity Analysis

The nested loops that iterate through the input array are the main factors determining the code's time complexity. The inner loop and its maximum operation add to the O(k) time complexity, while the outer loop operates in O(n) time. As a result, O(n * k) is the total time complexity.

For the arrays {currentSum} and {kthSums}, the dynamic memory allocation primarily affects the space complexity. {currentSum} has an O(n) size, while `kthSums} has an O(k) size. O(n + k) is the total space complexity as a result. The constant space utilized for variables inside functions and the main program has an impact on the space complexity as well.

Priority Queue Approach

Using a priority queue (heap) to keep track of the K largest sums is another effective method. We update the heap with the current sum as we iterate through the array. The K-th largest sum is always found in the top element of the heap.

Code

#includ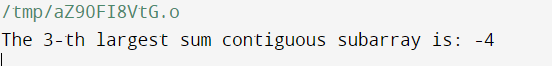e <stdio.h>
#include <stdlib.h>
struct HeapNode {
    int sum;
    int i;
    int j;
};
void swap(struct HeapNode *x, struct HeapNode *y) {
    struct HeapNode temp = *x;
    *x = *y;
    *y = temp;
}
void minHeapify(struct HeapNode *minHeap, int i, int heapSize) {
    int smallest = i;
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;

    if (leftChild < heapSize && minHeap[leftChild].sum < minHeap[smallest].sum) {
        smallest = leftChild;
    }
    if (rightChild < heapSize && minHeap[rightChild].sum < minHeap[smallest].sum) {
        smallest = rightChild;
    }
    if (smallest != i) {
        swap(&minHeap[i], &minHeap[smallest]);
        minHeapify(minHeap, smallest, heapSize);
    }
}
void buildMinHeap(struct HeapNode *minHeap, int heapSize) {
    int i = (heapSize - 1) / 2;
    while (i >= 0) {
        minHeapify(minHeap, i, heapSize);
        i--;
    }
}
int kthLargestSumSubarray(int arr[], int n, int k) {
    struct HeapNode *minHeap = (struct HeapNode *)malloc(sizeof(struct HeapNode) * k);
    int *currentSum = (int *)malloc(sizeof(int) * n);
    currentSum[0] = arr[0];
    int heapSize = 0;
    for (int i = 1; i < n && i <= k; i++) {
        minHeap[heapSize].sum = currentSum[i - 1] + arr[i];
        minHeap[heapSize].i = i - 1;
        minHeap[heapSize].j = i;
        heapSize++;
        currentSum[i] = currentSum[i - 1] + arr[i];
    }
    buildMinHeap(minHeap, heapSize);
    for (int i = k; i < n; i++) {
        if (arr[i] > minHeap[0].sum) {
            currentSum[i] = arr[i];
        } else {
            currentSum[i] = minHeap[0].sum;
            minHeap[0].sum = currentSum[i];
            minHeap[0].i = i;
            minHeap[0].j = i;
            minHeapify(minHeap, 0, heapSize);
        }
        for (int j = heapSize - 1; j > 0; j--) {
            int parent = (j - 1) / 2;
            if (minHeap[j].sum + currentSum[i] < minHeap[parent].sum) {
                swap(&minHeap[j], &minHeap[parent]);
            }
        }
    }
    int result = minHeap[0].sum;
    free(minHeap);
    free(currentSum);
    return result;
}
int main() {
    int arr[] = {4, -8, 9, -4, 1, -8, -1, 6};
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 3;
    int result = kthLargestSumSubarray(arr, n, k);
    printf("The %d-th largest sum contiguous subarray is: %d\n", k, result);
    return 0;
}

Output:

Code Explanation

Min Heap Structure

To represent a node in a min heap, the code defines a struct HeapNode. It has fields for the subarray's indices, i and j, as well as the sum.

Swap Function

To switch between two HeapNode structures, a swap function is defined.

Min Heapify Function

The min-heap property is upheld by the minHeapify function. It recursively compares a node with its offspring and switches them if necessary.

Construct a Min Heap Function

The buildMinHeap function uses minHeapify repeatedly to create a min heap from an array.

K-th Biggest Subarray Function for Sum

The primary function, kthLargestSumSubarray, efficiently tracks the K-th largest sums by using a min-heap.
Memory is dynamically allocated for currentSum and minHeap.
Adds the first K elements to the min heap.
Updates the heap and currentSum as it iteratively goes through the remaining elements.
At the top of the min heap is the K-th largest sum.

Main Function

The main function initializes an array, its length, and the value of K.
Makes use of the array, length, and K parameters to invoke the kthLargestSumSubarray function.

Time and Space Complexity Analysis

The time complexity and space complexity of the code, which finds the K-th Largest Sum Contiguous Subarray, are O(n * log(k)) and O(k), respectively, where 'n' is the length of the input array. The iteration through the array and the min heap operations impact the time complexity. In contrast, the dynamic memory allocation for the min heap is the main cause of the space complexity. Using a min heap, the code effectively maintains the K-th largest sums, handling large datasets with less time and space overhead than brute-force approaches.

Next TopicNumbsubarrayer of elements less than or equal to a given number in a given

← prev next →