Two dimensional Binary Indexed Tree or Fenwick TreeA sophisticated data structure called a two-dimensional binary indexed tree (2D BIT), often referred to as a Fenwick tree, is used to quickly update and query a two-dimensional array (matrix) by keeping cumulative sums or frequencies. The 2D BIT extends this idea to a two-dimensional setting, similarly to the one-dimensional BIT, which effectively computes prefix sums in a linear array. It enables quick updates and range queries for a two-dimensional matrix. This can be very helpful in applications like image processing, dynamic programming, and various mathematical techniques where cumulative data needs to be maintained in a grid-like format. Two indices, row and column, are used in the 2D BIT structure. The fundamental concept is to visualize the cumulative sums (or frequency) of values across different matrices. The efficient traverse of the BIT to compute cumulative sums and carry out updates is made possible by the way the indices are handled utilizing bitwise operations. Here is a explanation of how a 2D BIT works:
define the Dimensions of the 2D Matrix: You must specify the dimensions of the 2D matrix for which the 2D BIT is to be created. Assume the matrix has max_x (maximum rows) and max_y (maximum columns) dimensions. Create a 2D BIT array: Initialize a 2D array with the name BIT that has the dimensions (max_x + 1) (max_y + 1). All of the values are set to 0. To accommodate 1-based indexing, which is frequently used with BIT, the dimensions are raised by 1. BIT Update and Query Functions Definition: The 2D BIT and query cumulative sums will be updated using the getSum and updateBIT methods, respectively. In contrast to the 1D BIT, these functions now take into account both row and column indices. Initialize the 2D BIT: Create the 2D BIT from scratch by updating it for each element of the original matrix. If you already have a 2D matrix called matrix, you can use the updateBIT method to loop through it and update the associated cells in the 2D BIT.
Update function: In a 2D BIT, the update operation entails adding a value to a particular cell in the BIT array and propagating the impact of this update through the data structure to maintain cumulative sums. Bitwise Operations: To efficiently move across the 2D BIT, bitwise operations, notably bitwise AND (&) and the two's complement (-), are used. Update Procedure: Suppose you wish to add a value val to the value at the original matrix's point (x, y). You can perform the update as follows: Both the outer and inner while loops iterate across rows and columns, respectively. Add the update value val to each cell (x, y) in the BIT array. In order to move to the following appropriate cell in the same row or the following row, respectively, use the phrases y & -y and x & -x. Example of update operation: Let's say you wish to add 5 to the value in the original matrix at position (2,). The updateBIT function would be invoked as follows: updateBIT(2, 3, 5) The update procedure would propagate this change via the pertinent cells, adding 5 to cell (2, 3) in the BIT array. In order to facilitate effective range sum queries, this update procedure makes sure that the cumulative sums are accurately kept in the BIT structure. These update processes allow the 2D BIT to quickly calculate cumulative sums while accurately reflecting changes to the original matrix.
Calculating the sum of values within a certain sub-matrix of the original matrix is the query operation in a 2D BIT. To do this, subtract the cumulative sums of the excluded regions, then add the double excluded region back in. Bitwise Operations: To efficiently navigate through the 2D BIT, bitwise operations (bitwise AND & and two's complement -) are used, similar to the update operation. Query Process: Suppose you wish to find the sum of values in a sub-matrix in the original matrix that is defined by the bottom-left corner (x1, y1) and the top-right corner (x2, y2). Both the outer and inner while loops iterate across rows and columns, respectively. You add the value of each cell (x2, y2) in the sub-matrix to the total. To move to the previous relevant cell in the same row or the previous row, respectively, use the phrases y2 & -y2 and x2 & -x2. Subtraction and addition: You use the method shown below to determine the sum inside a submatrix defined by (x1, y1) and (x2, y2): sum_submatrix = queryBIT(x2, y2) - queryBIT(x2, y1 - 1) - queryBIT(x1 - 1, y2) + queryBIT(x1 - 1, y1 - 1) queryBIT(x2, y2) gives the sum of the entire sub-matrix. queryBIT(x2, y1 - 1) subtracts the sum of the excluded top-right corner. queryBIT(x1 - 1, y2) subtracts the sum of the excluded bottom-left corner. queryBIT(x1 - 1, y1 - 1) adds back the sum of the doubly-excluded top-left corner. Algorithm: We think about the example below. Let's say we need to calculate the sum of all the numbers in the highlighted area. 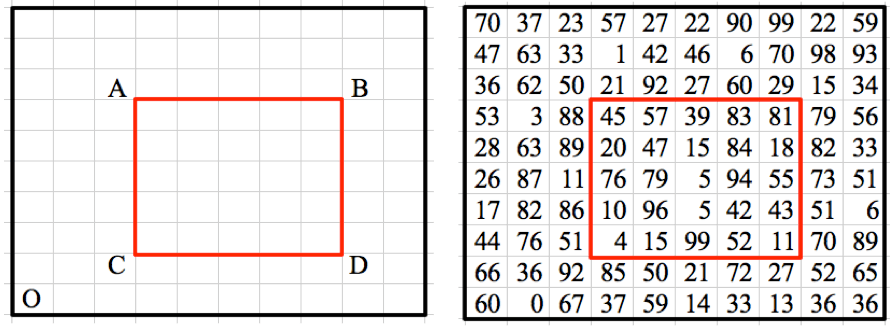
We consider O to be the matrix's origin at the bottom.A 2D BIT then takes advantage of this by: Sum beneath the highlighted region is equal to Sum(OB) + Sum(OD) + Sum(OA) + Sum(OC) 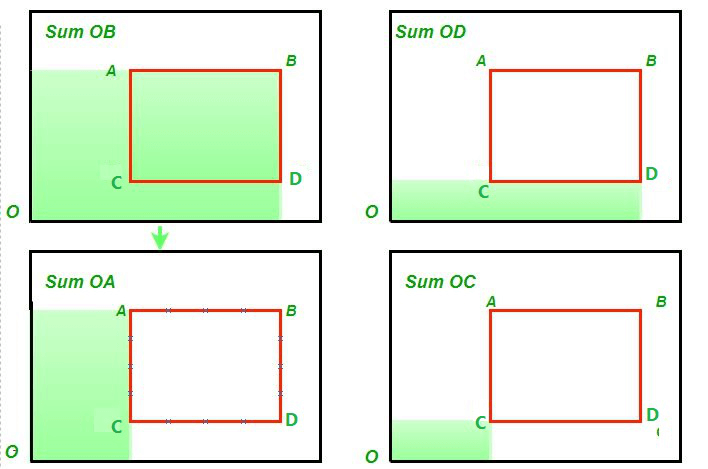
The getSum(x, y) function, which calculates the sum of the matrix from (0, 0) to (x, y), is used in our software. Thus, the following formula: Sum in the highlighted region equals Sum(OB) - Sum(OD) Sum(OA) minus Sum(OC) The result of the above formula is, getSum(x2, y2) = getSum(x2, y1-1) - getSum(x1-1, y2) + getSum(x1-1, y1-1) is the formula for the query (x1, y1, x2, y2). where the coordinates for C are x1, y1, and y2, and those for B are x2, y2, and y. All elements within the area of (x, y) to (N, M) are updated by the updateBIT(x, y, val) function, where N is the maximum X coordinate for the entire matrix. M is the highest Y coordinate in the entire matrix. The resting process is quite comparable to the 1D Binary Indexed Tree process. Implementation: In python: Output: Query (1, 1, 3, 2) = 30 Query (2, 3, 3, 3) = 8 Query (1, 1, 1, 1) = 1 The sub-matrix [(1, 1), (3, 2)]'s values are added up in query (1, 1, 3, 2), and the result is 3 + 8 + 1 + 6 + 7 + 5 = 30. The sub-matrix [(2, 3), (3, 3)]'s values are added up by query (2, 3, 3, 3), which yields the result of 7 + 5 = 12. The sub-matrix [(1, 1), (1, 1)]'s sum of values is 1, as determined by query (1, 1, 1, 1). The application effectively calculates these findings using the 2D Binary Indexed Tree (2D BIT).
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









