How do you implement Stack using Priority Queue or Heap?

The Stack is a basic data structure widely used in programming and computer science. Elements are added to and deleted from the top of the Stack according to the last-in, first-out (LIFO) principle. A priority queue or heap can efficiently implement a stack, even though they are most frequently built using a dynamic array or linked list. Newer items have a greater priority in these implementations because elements are prioritized based on their insertion order. In doing so, items follow the essential behaviour of a stack and emerge from the priority queue or heap in LIFO order. This article explains how to create a simple stack that can be efficiently executed in O(log n) steps by employing a priority queue or heap.

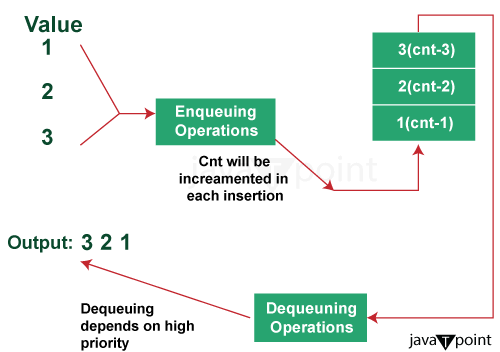
Stacks, Priority Quest and Minimum Heaps

Let's Revise the Concepts of Stack, Priority Queues and Heaps. In this case, we'll use Minimum Heap.

Stacks:

• A linear data structure models a real-world stack with two primary operations - push and pop.
• Push adds an element to the top of the Stack. Pop removes the element from the top.
• Stacks follow a LIFO (Last in, First out) order, meaning the most recently added element is removed first.
• Stacks have an abstract data type with key functions like push(), pop(), peek(), and isEmpty().
• They are commonly implemented using an array or linked list. An index or pointer tracks the top element.
• Applications include Undo/redo functions, compiler syntax checking for matching brackets, and browser back/forward navigation.

Priority Queues:

• A priority queue is an abstract data type like a regular queue, but each element has a priority value.
• Elements are dequeued in priority order - higher priority elements are served before lower priority ones.
• Priority queues require two key operations - insert (enqueue) and remove/access the highest priority (dequeue).
• Priority queues are commonly implemented using heaps, which provide logarithmic time operations.
• Elements in the heap are ordered by their natural ordering or a custom comparator.
• Applications include Task scheduling, algorithms like Dijkstra's, and finding minimum spanning trees.

Min Heaps:

• A min-heap is a complete binary tree that satisfies the heap property - each node's value is less than or equal to its children.
• The root node contains the minimum value in the tree. Elements can be efficiently enqueued and dequeued in logarithmic time.
• Min heaps implement the required operations of a priority queue efficiently.
• Key operations are peek (get min), insert, extractMin (remove min), and decrease key.
• Min heaps are typically implemented using arrays. Child and parent nodes are related mathematically.
• Used to implement priority queues, graph algorithms like Dijkstra's, and sorting algorithms like heapsort.

Advantages of using Priority Queues and Min Heaps for Implementing Stacks over Normal Arrays and Linked Lists]

Efficiency:

• With a min heap or priority queue, fundamental stack operations like push and pop can be implemented in O(log n) time. This is a significant efficiency gain compared to the O(1) time for arrays and linked lists.
• The heap structure provides logarithmic time complexity for insertion and deletion. The heap property only requires bubble down/sift down and bubble up/setup operations.
• Even though logarithmic time is slightly slower than constant time, it performs excellently for most applications. Searching through log n elements is still very fast.
• Heaps are more efficient than arrays because no resizing or copying of elements is required. Extra capacity doesn't need to be allocated.

Flexibility:

• Priority queues allow elements to be inserted in any priority order, not just LIFO order like stacks. This provides more flexibility.
• Custom comparators can be implemented to order elements based on application-specific criteria, not just natural ordering.
• Heaps intrinsically implement a priority order and provide an abstract data type. The implementation details are hidden.
• Unlike arrays, heap operations like push/pop don't need direct access to indexes or specific elements.

Memory Usage:

• Heaps only require a single array (plus a small amount of bookkeeping variables) to implement the priority queue. Very memory efficient.
• No need to allocate next/previous pointers like in linked lists. Overhead per element is low.
• The heap data structure consolidates elements in a dense array-based structure. Less scattered memory allocation.
• Space complexity is O(n) for heap priority queues versus O(n) for arrays/linked lists. But constant factors are lower.

Reusability:

• Heap code can be reused across applications needing priority queue features since it's an abstract data type.
• Heaps are used in algorithms like Dijkstra's, so an implementation can serve multiple purposes.
• Encapsulating the heap logic into a separate class promotes reusability across projects.
• Priority queues are a standardized data structure so heap implementations will be portable across languages.

How to Implement the Stack?

Algorithm:

1. Create a min heap or priority queue data structure to store the stack elements.
2. Create an empty min heap/priority queue to initialize an empty stack.
3. To push an element onto the Stack, insert the element into the heap/priority queue. The priority is set based on the element's insertion order (newer elements have higher priority).
4. To pop an element of the Stack, remove and return the highest priority element from the heap/priority queue. This will remove the element most recently added.
5. To peek at the top element, return the highest priority element from the heap/priority queue without removing it.
6. Check if the heap/priority queue is empty to implement isEmpty() for the Stack.

Approach:

• Use a min heap to implement the priority queue efficiently based on insertion order priorities.
• Use an array to represent the elements in the heap. Calculate indices of parent/child nodes mathematically.
• Write helper methods for siftUp to insert, siftDown to remove, peek for getting min.
• Enqueue with siftUp and dequeue with siftDown to keep the min heap ordered.
• Track priority/insertion counts separately from elements to assign priorities.
• Encapsulate the heap in a priority queue/stack class with public push/pop/peek methods.
• Use comparable interfaces or custom comparators if ordering is more complex than insertion order.
• Consider capacity limits, dynamic resizing, and other optimizations if large stacks are required.
• Write unit tests to validate LIFO behaviour and edge cases.

Output:

Explanation of the Python Program

MinHeap Class:

• init() initializes the underlying heap list with a dummy element at index 0. This simplifies child/parent calculations. Size is set to 0.
• swap() is a helper method to swap two elements in the heap list by index. Bubbling operations use this.
• push() takes an item, appends it to the heap list, increments size, and calls bubbleUp() to maintain the heap order. Insertion logic is handled by __bubbleUp().
• pop() stores the root element, replaces the root with the last element, decrements the size, pops the last element, and bubbles down the new root. Delete logic is in __bubbleDown().
• peek() simply returns the root element at index 1 in constant time.
• bubbleUp() recursively compares the inserted element with its parent, swapping if less than a parent. This percolates the element up to the correct position.
• bubbleDown() compares roots with children, swapping with smaller children. Recursively repeats to bubble down to the correct spot.

Stack Class:

• init() initializes an empty MinHeap to store stack elements.
• push() calls the heap's push() method to insert while maintaining min heap ordering.
• pop() calls the heap's pop() method which removes min element. This removes the most recently added element, like a stack.
• peek() just proxies to the heap's peek() to return the top element.
• is_empty() checks if the heap size is 0 to see if the Stack is empty.

So, in summary, the key logic is that the MinHeap acts as a priority queue ordered by insertion time. Using it as the underlying data store, the Stack methods exhibit LIFO behaviour since the newest elements have the highest priority in a heap.