In place, convert BST into a Min-HeapProblem Statement: Transform a Binary Search Tree into a Min-Heap with the same elements, utilizing an in-place approach and achieving this conversion in linear time complexity (O(n)). Input: Output:
8
/ \
10 17
/ \ / \
15 12 20 25
Likewise, the answer might be anything that follows the principles of Min-Heap. Note: Before looking into the solution, try to come up with an approach firstMethod 1: Naive approach: Using extra space:
Pseudo Code: Note: Try to implement without looking into the original code to improve your standards of coding by referring to the above-mentioned pseudo code if it got stuck in between and cross-check the solution provided to review the multiple ways of writing the code.By employing this approach, we ensure that the Binary Search Tree is transformed into a Min-Heap with the specified conditions, maintaining the integrity and order of elements accordingly. Java Implementation of the above approach Output: 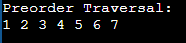
Explanation:
Time Complexity: O(N) Space Complexity: O(N) Since the above approach makes use of auxiliary space, you need to optimize the solution further. Method 2: (Optimal) When permitted to utilize additional memory, we can execute an inorder traversal of the tree and record the keys in a separate array. This array will naturally be sorted due to the properties of the BST. Subsequently, we can create a complete binary tree by traversing the sorted array and constructing nodes level by level, from left to right. By selecting the next minimum element from the sorted array, we guarantee that the resultant binary tree adheres to the min-Heap property. This method achieves a time complexity of O(n) but necessitates extra space for array storage, making it a non-in-place solution." "To achieve an in-place transformation of a binary search tree into a sorted linked list, we employ a reverse inorder traversal. This involves traversing the BST in a manner that prioritizes the right subtree before the left subtree. As we traverse, we insert nodes at the beginning of the existing linked list and adjust the head pointer accordingly. By performing this reverse inorder traversal and carefully managing node insertions, we maintain the sorted order of the linked list. This method ensures an efficient use of memory without relying on additional data structures." "Subsequently, we proceed to convert the sorted linked list into a min-Heap. This transformation involves carefully adjusting the left and right pointers of the nodes to adhere to the min-Heap properties. To accomplish this, we conduct a level order traversal of the partially constructed min-Heap Tree. Simultaneously, we traverse the linked list in sync with this traversal. At each step, we designate the parent node from the queue, assigning the next two nodes from the linked list as its children. These newly assigned nodes are then enqueued for further processing. This process, supported by the sorted nature of the linked list, guarantees the preservation of the min-heap property." Hope you understand this approach; below is the detailed algorithm for your logical understanding Algorithm to Convert BST to Min-Heap In-Place: Step 1: Define Node Structure Define a structure Node with integer data and pointers to left and right children. Step 2: Define Utility Functions Define a utility function newNode(data) to create a new node with the given data, initializing left and right pointers to NULL. Step 3: Convert BST to Sorted Linked List Define a function BSTToSortedLL(root, head_ref) to convert the BST to a sorted linked list using reverse inorder traversal. Base Case: If root is NULL, return. Recursively call BSTToSortedLL(root.right, head_ref). Update pointers to convert the tree to a linked list. Step 4: Convert Sorted Linked List to Min-Heap Define a function SortedLLToMinHeap(root, head) to convert the sorted linked list to a Min-Heap using a queue. Base Case: If the head is NULL, return. Initialize a queue. Start with the first node as the root of the Min-Heap. Traverse the linked list and use a queue to set the left and right child pointers. Java Implementation of the above approach Output: 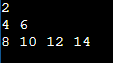
Time Complexity: O(n) Auxiliary Space: O(n)
Next TopicPolish and Reverse Polish Notation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










