Differences between Insertion Sort and Selection Sort
In computer science, sorting is a fundamental function that is essential for many different applications, such as organizing data for quick retrieval and improving algorithms. Several sorting algorithms are available, each with a methodology and set of performance properties. The two well-known sorting algorithms Insertion Sort and Selection Sort will be discussed in this essay. We will examine the specifics of how these algorithms function, their benefits and drawbacks, and the circumstances in which one might be chosen over the other.
Introduction
Understanding the importance of sorting algorithms in computer science before delving into the specifics of Insertion Sort and Selection Sort. Rearranging a group of objects or pieces into a specific order-ascending or descending-based on some criterion, usually a comparison of the components, is the process of sorting. The efficiency and effectiveness of various algorithms, search processes, and data storage can all be considerably improved by having properly sorted data.
There are many sorting algorithms available, and the choice of one depends on the dataset's size, the way the data is distributed, and the available resources. In this essay, we will concentrate on two very straightforward but significant sorting algorithms: Insertion Sort and Selection Sort.
Insertion Sort
A fundamental sorting method called Insertion Sort works best for tiny datasets or when the input is mostly sorted. Due to its simplicity, it is simple to implement and a great option when there is a small amount of input. The fundamental principle of the Insertion Sort is to keep a section of the dataset sorted while inserting each element from the unsorted component into the sorted portion at the proper location.

How Insertion Sort Works
- Initialization: The procedure is predicated on the notion that the initial piece has already undergone sorting. The second part is then covered.
- Insertion: For each additional element, Insertion Sort compares it to the elements in the sorted area and, if necessary, moves the larger elements to the right until the element is inserted in the proper location.
- Repeat: Till the full array is sorted, repeat steps 1 and 2 as necessary.
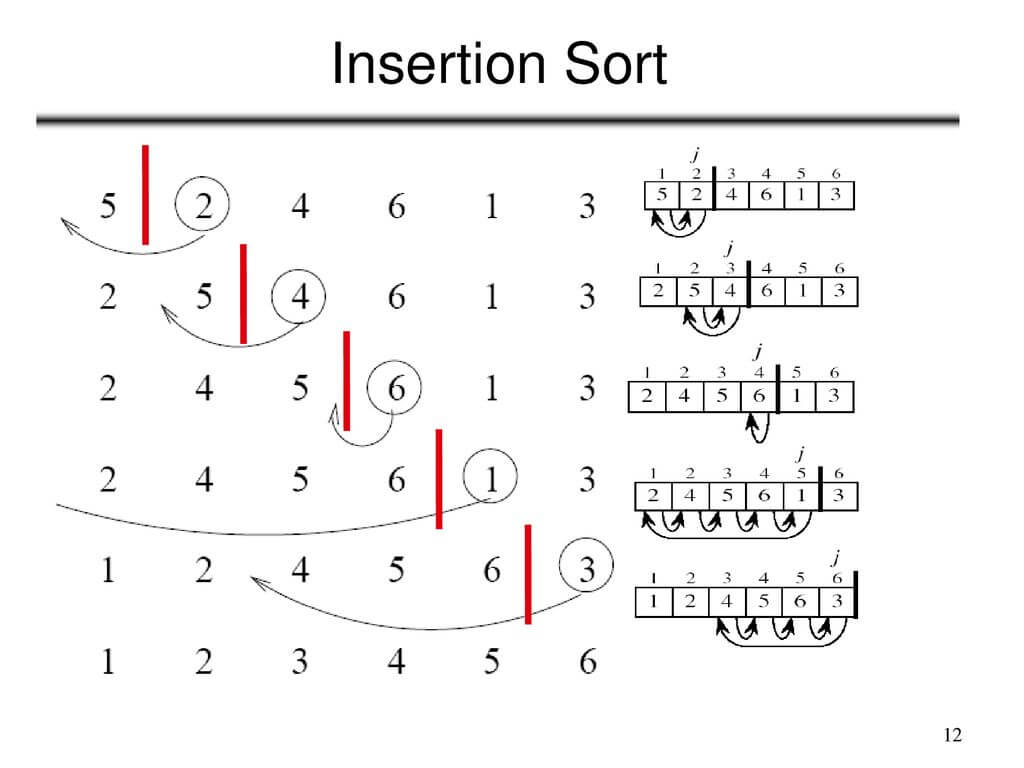
Let's look at a straightforward example to see how Insertion Sort functions. Take into account the unsorted array [5, 2, 9, 3, 6]. The algorithm works in the following way:
- It assumes this is sorted, beginning with element 5 in the list.
- When it comes to the second element (2), it swaps 2 and 5 and compares the results to produce [2, 5, 9, 3].
- The third element (9) is positioned correctly to form [2, 5, 9, 3, 6] by being compared to the sorted section (2, 5).
- We get [2, 3, 5, 9, 6] once the fourth element (3) is shifted into the proper location within the sorted section.
Advantages of Insertion Sort
- Simple Implementation: Insertion Sort is a suitable option for educational reasons and when simplicity is necessary because it is simple to implement and comprehend.
- Efficiency for tiny Datasets: Because there aren't many comparisons and swaps, the performance is okay for tiny datasets or when the input is mostly sorted.
- Insertion: Adaptive Sort is a good fit for partially sorted data since it avoids duplicating work by leaving elements in their proper placements.
- Insertion of In-Place Sorting: Sort is an in-place sorting algorithm, so sorting doesn't take up additional memory space.
Disadvantages of Insertion Sort
- Inefficient for Large Datasets: The number of comparisons and swaps grows quadratically as the size of the dataset increases, leading to subpar performance for larger inputs.
- Lack of Parallelism: Insertion Sort is less compatible with contemporary multi-core CPUs because it does not inherently facilitate parallel processing.
- Stability: The order of equal items is preserved, making it a stable sorting algorithm. However, it is not as effective at preserving stability as other sorting algorithms, such as Merge Sort.
Selection Sort
Similar to Insertion Sort, Selection Sort is a simple sorting algorithm that is simple to comprehend and use. It works by splitting the input list into two sections: the sorted section at the start, and the unsorted section at the end. The algorithm repeatedly chooses the least (or maximum) element from the unsorted segment and inserts it at the end of the sorted portion.
How Selection Sort Works
- Initialization: At first, all of the elements are present in the unsorted portion, but the sorted portion is empty.
- Selection: The algorithm searches the unsorted segment for the minimum (or maximum) element and replaces it with the unsorted portion's leftmost element.
- Expansion: The unsorted portion is reduced by one element, while the sorted portion is expanded to incorporate the newly chosen minimum (maximum) element.
- Repeat: Till the full array is sorted, repeat steps 2 and 3 as necessary.
The same unsorted array [5, 2, 9, 3, 6] will be used to demonstrate how Selection Sort functions.
- In the first pass, the leftmost element (5) is switched to the minimum element (2), resulting in the numbers [2, 5, 9, 3, 6].
- The minimal element (3) is chosen from the remaining unsorted area in the second pass and swapped with 5, resulting in [2, 3, 9, 5, 6].
- The array [2, 3, 5, 6, 9] is completely sorted as a result of this operation.
Advantages of Selection Sort
- Simple Implementation: Selection Sort is similarly straightforward to use and understand as Insertion Sort.
- In-Place Sorting: It is an in-place sorting method, therefore there is no need for additional RAM to store the sorted data.
- Stable: Choice Sort is beneficial in some situations when stability is important since it maintains the relative order of equal elements.
- Minimal Data Movement: Selection Sort only needs one element exchange per pass, as opposed to Insertion Sort, which may require numerous element swaps. This may be advantageous when changing out components would be expensive.
Disadvantages of Selection Sort
- Inefficiency: Picking Due to its time complexity, which is O(n2), where n is the number of elements in the input, sorting is inefficient for huge datasets. This means that when sorting huge arrays, it performs poorly.
- Lack of Adaptivity: Selection Sort does not adjust to the input data; regardless of the data's original order, it executes the same number of comparisons and swaps.
- Lack of Parallelism: Selection Sort's performance on multi-core processors is constrained since, like Insertion Sort, it does not come with a built-in parallel processing capability.
Differences between Insertion Sort and Selection Sort
| Insertion Sort |
Selection Sort |
| Maintain a portion that is sorted, and add components from the unsorted portion to the sorted part in the appropriate places. |
Separate the input into sorted and unsorted parts. Select the least (or maximum) element repeatedly, then transfer it from the unsorted to the sorted portion. |
| In the best-case scenario, the array's temporal complexity is (N) when it is already arranged ascendingly. It has (N2) in both the worst and average scenarios. |
There is complexity (N2) for the best case, worst case, and average selection sort. |
| More flexible (Effective with incompletely sorted data) |
Less adaptable (performs the same number of processes in any order) |
| In this sorting method, there are fewer comparison operations than swapping operations. |
This sorting algorithm performs more comparison operations than swapping operations combined. |
| As opposed to the Selection sort, it is more effective. |
Compared to the Insertion sort, it is less effective. |
| It is a stable algorithm |
It is an unstable algorithm |
| Small datasets are suitable, especially when the data is partially sorted. Basis for more sophisticated sorting algorithms. |
due to inefficiency, rarely applied in real-world applications. when minimizing data movement is a top priority, it can be used. |
| The adaptability, simplicity, and effectiveness of Insertion Sort on partially sorted data are its main advantages. |
The main advantages of Selection Sort are its simplicity, stability, and performance predictability. |
| Due to its optimal linear time complexity, insert sort is effective on small datasets. |
Although the performance of Selection Sort is stable across input sizes, it is still not the best option for tiny datasets. |
Conclusion:
When the data is mostly sorted, insert sort is comparatively effective for small datasets. It is a great option for educational reasons and is straightforward to apply. Compared to Selection Sort, its adaptive nature allows it to perform better on partially sorted data.
Although likewise simple to understand, Selection Sort is less effective than Insertion Sort for small datasets and is not often suggested for sorting big arrays. However, in situations when element shifting is expensive, its minimum data movement may be favorable. Because of its stability, Selection Sort is a good choice when upholding the relative order of equal components is crucial.
In conclusion, the two basic building blocks of sorting algorithms are insertion sort and selection sort. Because they might not always be the best options for sorting huge datasets in real-world applications, they offer important information about the ideas and principles behind sorting, making them worthwhile topics for research and understanding of the principles behind sorting algorithms.
|





 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









