Given a n x n square matrix, find the sum of all sub-squares of size k x k

Problem Statement

Given a square matrix of size n x n and an integer k, we need to find the sum of all sub-squares of size k x k within the matrix.

For example, let's consider the following 4x4 matrix:

If k is 2, we need to find the sum of all 2x2 sub-squares:

Sub-square 1:

Sum = 1 + 2 + 5 + 6 = 14

Sub-square 2:

Sum = 2 + 3 + 6 + 7 = 18

... and so on for all possible 2x2 sub-squares.

Brute Force Approach

One straightforward approach is to iterate through all possible sub-squares of size k x k and calculate their sums individually. This involves nested loops to traverse the matrix and compute the sum for each sub-square. While this approach is intuitive, it has a time complexity of O(n^4), making it inefficient for large matrices.

Output: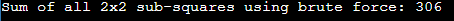

Time Complexity:

The time complexity of the brute force approach is determined by the nested loops used to iterate over all possible sub-squares of size k x k within the n x n matrix. The nested loops structure leads to a time complexity of O((n - k + 1)^2 * k^2).

The outer two loops iterate over (n - k + 1) rows and (n - k + 1) columns.

The inner two loops iterate over the k x k sub-square.

In the worst case scenario, when k is much smaller than n, the time complexity can be approximated to O(n^4). This is because the terms (n - k + 1)^2 and k^2 would contribute significantly compared to n^2.

Approach 2 :

Preprocessing for Efficient Computation

We can significantly improve the efficiency of our algorithm by using a preprocessing technique that computes the cumulative sum matrix. The idea is to create a new matrix where each cell (i, j) holds the sum of all elements in the sub-matrix that starts at (0, 0) and ends at (i, j) in the original matrix.

For example, given the matrix:

The cumulative sum matrix would be

Once we have the cumulative sum matrix, we can efficiently calculate the sum of any sub-square by utilizing the sums of its corner elements.

Efficient Approach

Compute Cumulative Sum Matrix: Iterate through the original matrix and build the cumulative sum matrix.

Calculate Sub-Square Sum: For each sub-square (i, j) of size k x k, calculate its sum using the cumulative sum matrix:

Here, cumSum[i+k][j+k] is the sum of the sub-matrix from (0, 0) to (i+k, j+k), and the other terms exclude the portions that are not part of the sub-square.

Output: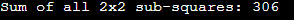

The key operations contributing to this time complexity are:

Building Cumulative Sum Matrix: The nested loops used to iterate through the entire matrix and calculate the cumulative sum at each cell take O(n^2) time.

Calculating Sub-Square Sums: The nested loops used to iterate through all possible sub-squares of size k x k take O((n - k + 1)^2) time. Since 'k' is typically smaller than 'n', the term (n - k + 1)^2 is dominated by the n^2 term, making the overall complexity O(n^2).

In summary, the time complexity of the code is O(n^2), which is a significant improvement over the brute force approach with a higher time complexity of O(n^4) for larger matrices and sub-square dimensions.