DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Bottom View of a Binary TreeThe nodes that are visible when a binary tree is seen from the bottom are known as the tree's "bottom view." To put it another way, it entails locating and displaying the nodes that would show up in the tree's lowest level while taking each node's horizontal distance and depth into account. The horizontal distance (HD) of each node from the root is taken into account to obtain the bottom view of a binary tree. The horizontal distance of the root is regarded as 0, and when we move left or right, the horizontal distance either reduces by 1 or grows by 1. The fundamental strategy for locating the bottom view entails traversing the tree in depth-first, noting the horizontal distance between each node, and storing the nodes for each horizontal distance. The node with the maximum depth-the last node encountered at each horizontal distance-is ultimately taken into account when determining the bottom view. Here is a step-by-step procedure for locating a binary tree's bottom view:
It's crucial to remember that the algorithm's precise implementation may change depending on the particular programming language and data structures employed. Bottom view of a binary tree in the algorithmThe root of the binary tree as an input 1. Create a map to store the nodes on the bottom view together with their depth and horizontal distance. 2. Move through the binary tree depth-first. - Add the node's value and depth to the map for each node for the relevant horizontal distance. - Increase and decrease the horizontal distances that were encountered during the traversal. 3. Choose the nodes on the map that have the greatest depth for each horizontal distance when you iterate over it to get the bottom view nodes. 4. Show the nodes on the bottom view. Pseudocode:1. Create an empty map to store the nodes for the bottom view using the bottom view (root) procedure. bottomTraverseTree ViewMap(root, 0, 0, bottomViewMap) DisplayBottomView(bottomViewMap) 2. Node, horizontal_distance, depth, bottomViewMap; procedure TraverseTree In the event that the node is empty, return Where horizontal_distance is not in the bottom depth, or ViewMap must be greater than bottomViewMap[horizontal_distance].depth: the bottom(Node. value, depth) ViewMap[horizontal_distance] Node.left, horizontal_distance - 1, depth + 1, bottomViewMap; TraverseTree Node.right, horizontal_distance + 1, depth + 1, bottomViewMap; TraverseTree 3. DisplayBottomView(bottomViewMap) procedure For items in sorted(bottomViewMap), order the bottomViewMap by horizontal distance: Present entry.value Usage:To retrieve and display the bottom view of the binary tree, call the bottom view (root) with the binary tree's root. Code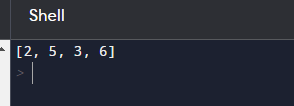
Next TopicCircular List Application
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









