Binary Search Tree Implementation

This article explains the many operations of a binary search tree application that has been coded in the C programming language. A binary search tree is a binary tree where each node's left subtree value is less than the node's value, which is less than each value in the right subtree.

In this article, we'll define a binary search tree and show you how to use the C programming language to accomplish various binary search tree operations.

A specific type of data structure called a tree is used to represent data in a hierarchical format. It can be described as a group of nodes-collections of things or entities-that are connected to one another to create the illusion of a hierarchy. Trees are non-linear data structures because their data is not organised in a linear or sequential manner.

The items are arranged in a binary search tree according to a certain order. A Binary search tree requires that the left node's value be less than the parent node and the right node's value be larger than the parent node. The left and right branches of the root are subject to this rule in a recursive fashion.

It is advised to first see a quick explanation of the Tree data structure before moving on to the binary search tree.

Basics of the Binary Search Tree in C

A binary search tree is a type of tree data structure that enables users to sort and store information. Because each node can only have two children, it is known as a binary tree. It is also known as a search tree because we can look up numbers in O(log(n)) time.

Typical characteristics of a binary tree are:

The root node is greater than all nodes in the left subtree.
The root node is outperformed in value by every node in the right subtree.
Each node's two subtrees are likewise binary search trees, therefore they have the aforementioned two characteristics.

Binary Search Tree Example

The diagram below shows two binary search trees, one of which complies with all of the requirements for a binary search tree while the other deviates from the standard.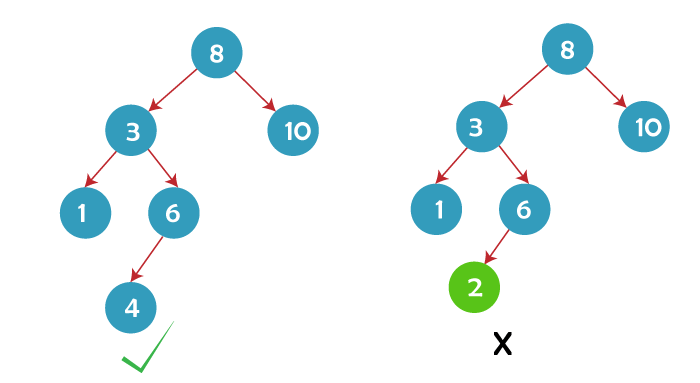

The right subtree of node 3 includes a value less than it, hence the binary tree on the right isn't a binary search tree.

How to Operate a Binary Search Tree in C

A binary search tree can be processed using three fundamental operations:

Operation 1: Search

We need to locate a particular piece in the data structure in Search. Because the elements are stored in sorted order in binary search trees, the searching process is made simpler.

The following is the algorithm for seeking an element in a binary tree:

Compare the searchable element to the tree's root node.
Return the root node if the value of the element being searched matches the value of the root node.
If the value is not the same, see if it is smaller than the root element, and if so, navigate to the left subtree.
Explore the appropriate subtree if it is greater than the root element.
Return NULL if the element isn't present throughout the entire tree.

With the aid of an example where we are attempting to search for an item having a value of 20, let's now explore search operation in a binary search tree code written in C:

Step 1: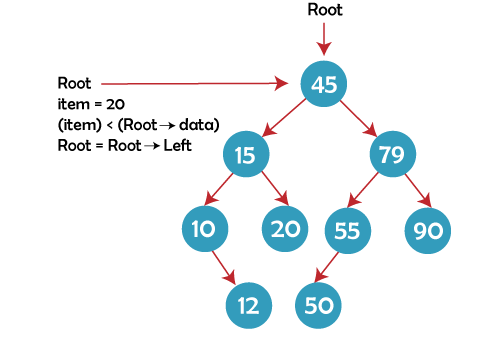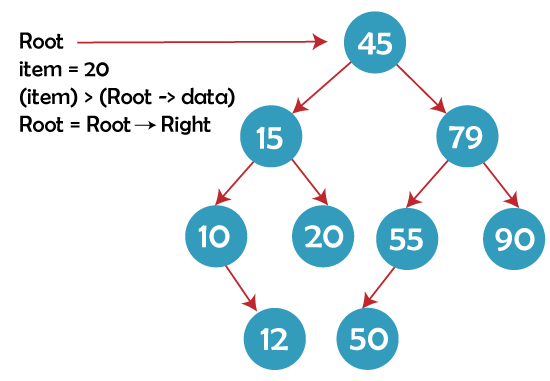

Step 2: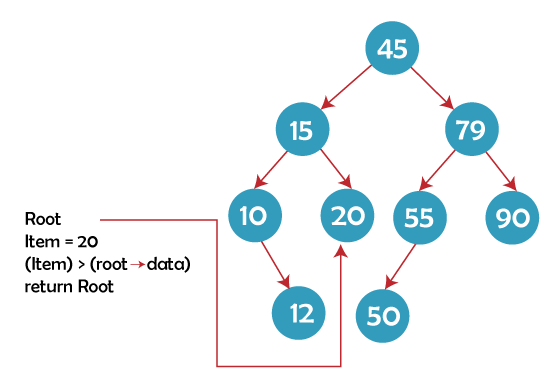

Operation 2: Insert

In a binary search tree, an element is always inserted at the leaf node. If the element to be inserted is smaller than the root value or the root node, we start our search operation from the root node and look for an empty position in the left subtree; otherwise, we look for the empty location in the right subtree.

The following is the algorithm for adding an element to a binary tree:

C Code:

   if node == NULL 
        return creatingNode(data)
   if (data < node -> data)
        node -> left  = insert(node -> left, data)
   else if (data > node -> data)
        node -> right = insert(node -> right, data)
   return node

Now that we have a specific instance where we are trying to insert an item with the value 65, let's examine how insertion works in a binary search tree: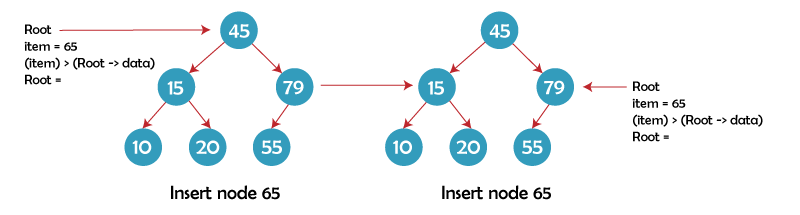

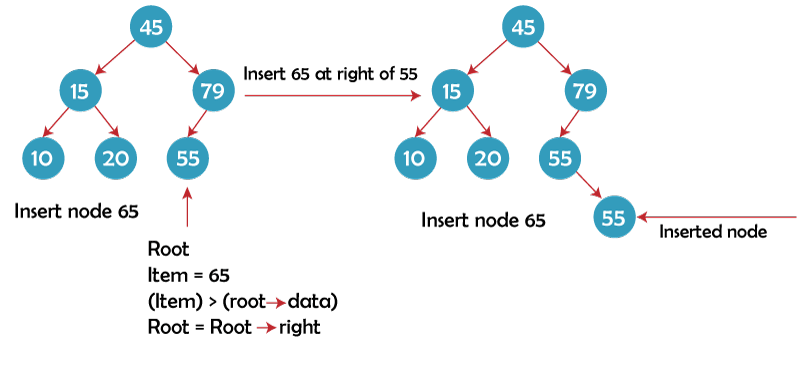
Operation 3: Deletion

A node from the binary search tree must be deleted during the deletion operation without violating any of its attributes. Deletion may happen in one of three situations:

1. Leaf node is the first node to be eliminated.

The simplest scenario for removing a node from a binary search tree is this one. Here, we'll swap out the leaf node for NULL and release the space that was allotted.

With the aid of an example that shows us to delete the node with a value of 90, we can better comprehend the deletion process in a binary search tree.

2. The deleted node has just one child node.

In this instance, the target node will be replaced with its child, which will then be deleted. As a result, the value to be erased will now be present in the child node. Therefore, to release the space allotted, we will simply replace the child node with NULL.

In the example below, a node with a value of 79 must be eliminated. Since this node has just one child, 55 will be used in its place.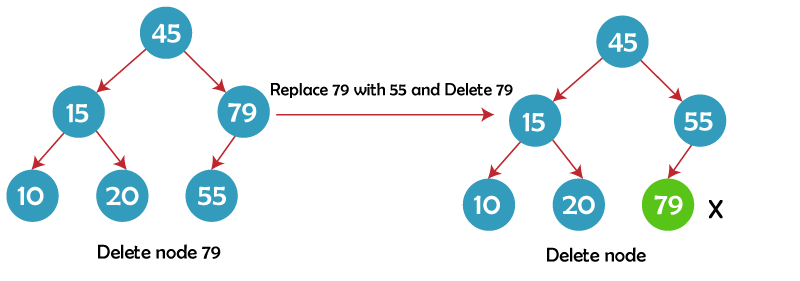

3. There are two children of the to-be-deleted node.

In comparison to the other two cases, this one is more complicated. Here, we do the following actions to remove the node:

We'll locate the target node's inorder successor so it can be removed.
Once the target node reaches the leaf, swap out this node for the successor.
NULL should be used in place of the target node to release the designated space.

In the example below, the root node, node 45, must be deleted. As a result, node 55 will be added in its place as the root node's immediate successor. Node 45 will now be near the tree's leaf, making it simple to delete.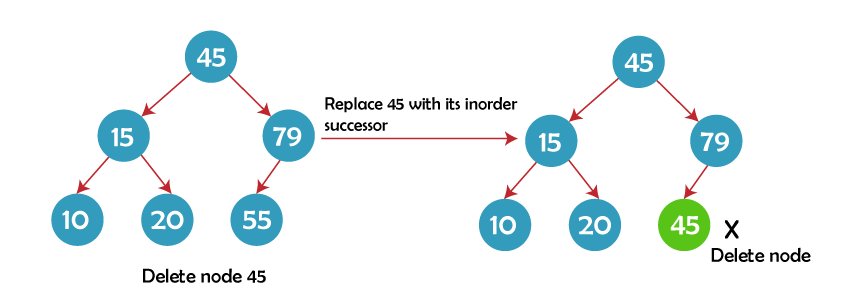

A C Program for Implementing a Binary Search Tree

Now let's use C programming to implement the formation of a node and traversals in Binary Trees. Here, we'll concentrate on actions that affect the binary search tree, such as insertion and deletion of nodes and searching.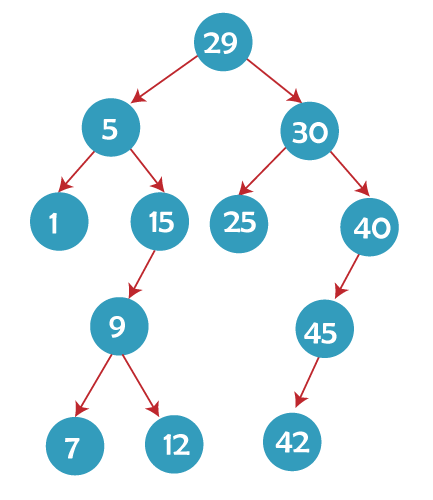

C Program:

#include <stdio.h>
#include <stdlib.h>

struct node {
  int data;
  struct node *right_child;
  struct node *left_child;
};

struct node* new_node(int x){
  struct node *temp;
  temp = malloc(sizeof(struct node));
  temp->data = x;
  temp->left_child = NULL;
  temp->right_child = NULL;

  return temp;
}

struct node* search(struct node * root, int x){
  if (root == NULL || root->data == x)
    return root;
  else if (x > root->data)
    return search(root->right_child, x);
  else
    return search(root->left_child, x);
}

struct node* insert(struct node * root, int x){
  if (root == NULL)
    return new_node(x);
  else if (x > root->data)
    root->right_child = insert(root->right_child, x);
  else 
    root -> left_child = insert(root->left_child, x);
  return root;
}
struct node* find_minimum(struct node * root) {
  if (root == NULL)
    return NULL;
  else if (root->left_child != NULL)
    return find_minimum(root->left_child);
  return root;
}

struct node* delete(struct node * root, int x) {

  if (root == NULL)
    return NULL;
  if (x > root->data)
    root->right_child = delete(root->right_child, x);
  else if (x < root->data)
    root->left_child = delete(root->left_child, x);
  else {
    if (root->left_child == NULL && root->right_child == NULL){
      free(root);
      return NULL;
    }
    else if (root->left_child == NULL || root->right_child == NULL){
      struct node *temp;
      if (root->left_child == NULL)
        temp = root->right_child;
      else
        temp = root->left_child;
      free(root);
      return temp;
    }
    else {
      struct node *temp = find_minimum(root->right_child);
      root->data = temp->data;
      root->right_child = delete(root->right_child, temp->data);
    }
  }
  return root;
}

void inorder(struct node *root){
  if (root != NULL) 
  {
    inorder(root->left_child); 
    printf(" %d ", root->data); 
    inorder(root->right_child); 
  }
}

int main() {
  struct node *root;
  root = new_node(20);
  insert(root, 5);
  insert(root, 1);
  insert(root, 15);
  insert(root, 9);
  insert(root, 7);
  insert(root, 12);
  insert(root, 30);
  insert(root, 25);
  insert(root, 40);
  insert(root, 45);
  insert(root, 42);

  inorder(root);
  printf("\n");

  root = delete(root, 1);

  root = delete(root, 40);

  root = delete(root, 45);

  root = delete(root, 9);

  inorder(root);
  printf("\n");

  return 0;
}

Output

1  5  7  9  12  15  20  25  30  40  42  45 
 5  7  12  15  20  25  30  42

Array Representation and Traversals in a Binary Search Tree Program Written in C

We will now use an array to create a binary search tree programme in C. A binary tree will be created in C using array representation, and inorder, preorder, and postorder traversals will then be implemented.

Consider the Following Array and Try to Create a Tree from It:

In the figure above, 0 stands for NULL. For example, node B's right and left children are both NULL, indicating that B is a leaf node.

C Program:

#include <stdio.h>

int max_node = 15;
char tree[] = {'\0', 'D', 'A', 'F', 'E', 'B', 'R', 'T', 'G', 'Q', '\0', '\0', 'V', '\0', 'J', 'L'};

int get_right_child(int index){
  if (tree[index] != '\0' && ((2 * index) + 1) <= max_node)
    return (2 * index) + 1;
  return -1;
}

int get_left_child(int index){
  if (tree[index] != '\0' && (2 * index) <= max_node)
    return 2 * index;
  return -1;
}

void preorder(int index){
  if (index > 0 && tree[index] != '\0'){
    printf(" %c ", tree[index]);
    preorder(get_left_child(index));
    preorder(get_right_child(index));
  }
}

void postorder(int index){
  if (index > 0 && tree[index] != '\0'){
    postorder(get_left_child(index));
    postorder(get_right_child(index));
    printf(" %c ", tree[index]);
  }
}

void inorder(int index){
  if (index > 0 && tree[index] != '\0'){
    inorder(get_left_child(index));
    printf(" %c ", tree[index]);
    inorder(get_right_child(index));
  }
}

int main() {
  printf("Preorder:\n");
  preorder(1);
  printf("\nPostorder:\n");
  postorder(1);
  printf("\nInorder:\n");
  inorder(1);
  printf("\n");
  return 0;
}

Output

Preorder:
 D  A  E  G  Q  B  F  R  V  T  J  L 
Postorder:
 G  Q  E  B  A  V  R  J  L  T  F  D 
Inorder:
 G  E  Q  A  B  D  V  R  F  J  T  L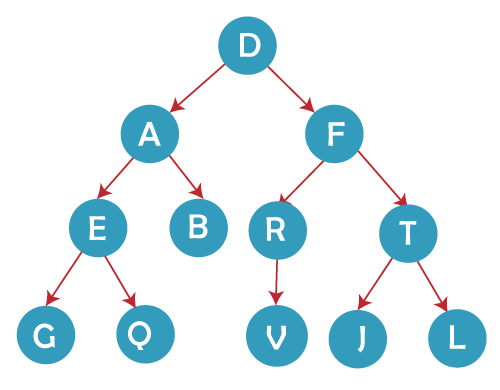

C Program for Binary Search Trees with Traversals and Linked List Representation

We will now use a linked list to implement a binary tree in C. A binary tree will be created in C using a linked list representation, and inorder, preorder, and postorder traversals will then be implemented.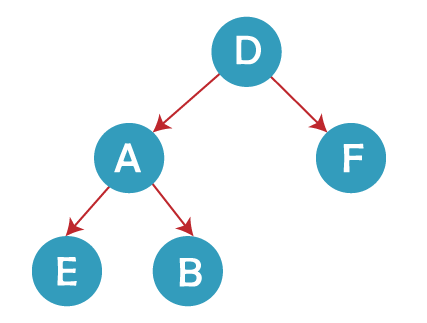

C Program:

    #include <stdio.h>
    #include <stdlib.h>

    struct node
    {
        char data;
        struct node *right_child;
        struct node *left_child;
    };

    struct node* new_node(char data)
    {
        struct node *temp;
        temp = malloc(sizeof(struct node));
        temp -> data = data;
        temp -> left_child = NULL;
        temp -> right_child = NULL;

        return(temp); 
    }

    void preorder(struct node *root)
    {
        if(root != NULL) 
        {
            printf(" %c ", root -> data); 
            preorder(root -> left_child);
            preorder(root -> right_child);
        }
    }

    void postorder(struct node *root)
    {
        if(root != NULL)
        {
            postorder(root -> left_child); 
            postorder(root -> right_child); 
            printf(" %c ", root -> data); 
        }
    }

    void inorder(struct node *root)
    {
        if(root != NULL) 
        {
            inorder(root -> left_child); 
            printf(" %c ", root -> data); 
            inorder(root -> right_child);
        }
    }

    int main()
    {
        struct node *root; 
        root = new_node('D'); 

        root -> left_child = new_node('A');
        root -> right_child = new_node('F'); 
        root -> left_child -> left_child = new_node('E'); 
        root -> left_child -> right_child = new_node('B');

        printf("Preorder:\n");
        preorder(root);
        printf("\n");
        printf("Postorder:\n");
        postorder(root);
        printf("\n");
        printf("Inorder:\n");
        inorder(root);
        printf("\n");

        return 0;
    }

Output

Preorder:
 D  A  E  B  F 
Postorder:
E  B  A  F  D 
Inorder:
 E  A  B  D  F

Binary Search Tree Complexity in C

Time Complexity

Insertion

Best case: O(logn)
Average case: O(logn)
Worst case: O(n)

Deletion

Best case: O(logn)
Average case: O(logn)
Worst case: O(n)

Searching

Best case: O(logn)
Average case: O(logn)
Worst case: O(n)

Space Complexity

Insertion: O(n)
Deletion: O(n)
Searching: O(n)

[The number of tree nodes in this case is n.]

Binary Search Tree in C Applications

Multilevel indexing is implemented in databases using binary search trees.
A binary search tree can be used for dynamic sorting.
The Unix kernel controls virtual memory regions via a binary search tree.

Conclusion

A binary search tree is a binary tree where each node's left subtree value is less than the node's value, which is less than each value in the right subtree.
Because the items are maintained in sorted order in a binary search tree, searching becomes easier.
In a binary search tree, the insertion operation is always carried out at the leaf node.
A binary search tree's deletion procedure contains three scenarios, including the following:
- The node to be destroyed has no children.
- The deleted node has one child.
- The node that will be removed has two kids.

So that's the end of the article. I sincerely hope you find this post to be educational and useful.

Next TopicFind Maximum Sum by Replacing the Subarray in Given Range

← prev next →