Tree Vertex Splitting in data structureOverviewTree vertex splitting is often used in tree-related algorithms, such as tree traversal algorithms, for example, bfs and dfs and tree decomposition algorithms, for instance, finding tree decompositions for graph problems and dynamic programming on trees. Tree Vertex SplittingIn the Design and Analysis of Algorithms (DAA) context, "tree vertex splitting" generally refers to a technique used in algorithms involving trees. One example of an operation that could be considered a tree split is found in a data structure with dynamic operations. This operation divides the tree containing vertex v into two parts by deleting the edge from v to its parent. This operation assumes that v is not a tree root. The Process of Vertex SplittingIn tree vertex splitting, a single vertex is divided into multiple vertices. Each new vertex retains one of the edges initially connected to the original vertex. This process results in a forest of trees, where each tree corresponds to one of the new vertices. Imagine you have a tree, a type of data structure where each node is connected. This method divides a tree into two parts based on parent-child relationships represented by links. Mathematical RepresentationMathematically, if we have a tree T and a vertex v in T, the vertex split operation on v results in a new graph T'. If v were of degree d in T, it would result in d new vertices in T', each of degree 1. In Tree Vertex Splitting, you choose a node in the tree. This selected vertex is then "split" or separated from the tree, resulting in two separate trees. The first one contains the chosen vertex and all vertices in the subtree rooted at this node. The second tree includes all the other vertices. For example, if we consider a tree with vertices 1, 2, 3, 4, and 5, 1 is the root with two children: 2 and 3. 2 has a child: 4. 3 has a child: 5. If we perform a Tree Vertex Splitting at node 3, we end up with two trees. The first tree contains vertices 3 and 5. The second tree has vertices 1, 2, and 4. 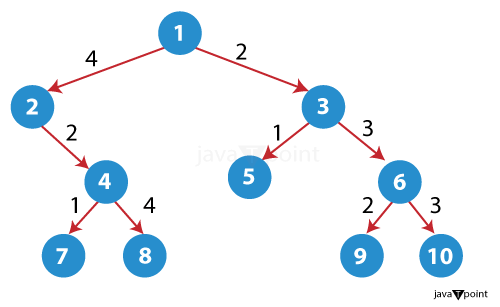
ApplicationsTree vertex splitting has various applications, such as placing flip-flops in partial scan designs, latches in pipelined circuits, signal boosters in courses and networks, and more. This technique divides networks into subnetworks for better efficiency and security. It simplifies complex problems in algorithms and is used in the greedy method for process scheduling in operating systems. Use in AlgorithmsTree vertex splitting is a fundamental operation used in many graph algorithms. It is beneficial in algorithms that deal with connectivity and network flow problems. By splitting vertices, these algorithms can simplify the problem and make it easier to find optimal solutions. Complexity AnalysisThe complexity of tree vertex splitting can vary depending on the specific algorithm or data structure used. For example, the time complexity of the vCover function is O(n), where n is the number of nodes in the binary hierarchical data structure. This is because each node is visited only once, and its vertex cover size is calculated in constant time. The space complexity of the program is O(n), where n is the number of nodes in the binary tree. Comparison with Other TechniquesTree vertex splitting can be compared with other techniques like the greedy and divide and conquer algorithms. The greedy algorithm builds up a solution piece by piece, always choosing the following article that offers the most prominent and immediate benefit. In the divide and conquer algorithm, the problem is broken down into small parts, called sub-problems, and then solved individually and combined to get the final solution. Other techniques include Traversal, Pruning, and Merging of trees. Each method has its use cases and trade-offs. The best technique depends on the specific problem you're trying to solve. ChallengesWhile tree vertex splitting is a powerful technique, it presents several challenges. The operation can significantly increase the graph's size, leading to increased computational complexity. Care must also be taken to ensure the algorithm correctly handles the split vertices. ConclusionTree vertex splitting is a powerful technique in graph theory that allows for the simplification of complex problems. By breaking down a single vertex into multiple vertices, we can transform a complex tree structure into a simpler forest of trees. This operation is particularly useful in algorithms dealing with connectivity and network flow problems. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









