Minimum number of subsets with distinct elements

We will provide an array or vector for the minimum number of subsets with distinct elements

in the question. We need to find out the minimum number of subsets to be done so that we don't have duplicate or repeating elements in any sub-set.

Let us take an example:

If the vector is vec = [1,2,3,3]

Now, we need to divide the above vector such that there should be no duplicate elements in each subset.

The possible ways are:

{1,2,3},{3}

Or

{3,1},{2,3}

Or

{2,3},{1,3}

By dividing into any of the two subsets, we made to have distinct elements in each subset, and our requirement is how many subsets need to be done to satisfy the condition.

We have done two subsets in the above case, so the answer is 2.

Now, we need to write the code to find the minimum number of subsets needed to make it:

CODE:

Output: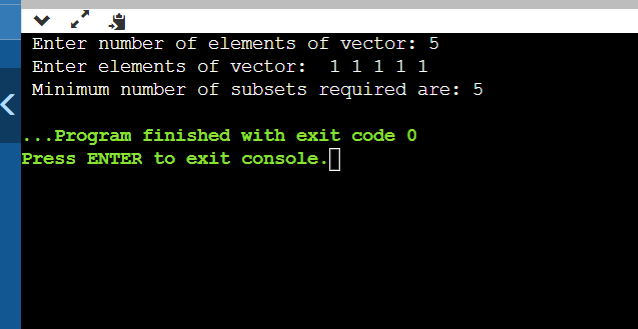

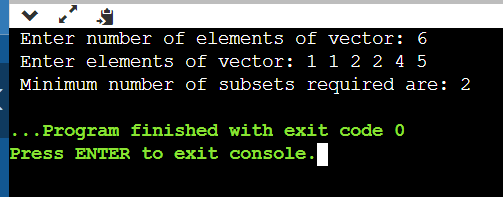
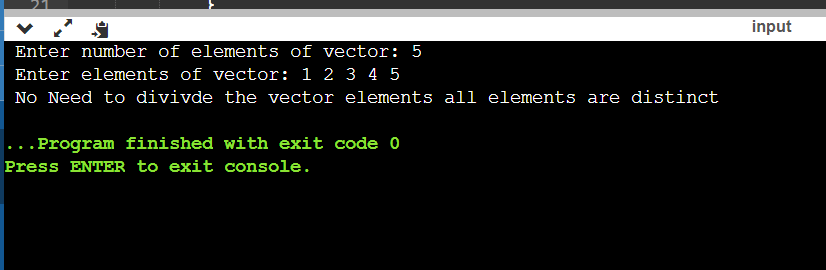
Explanation:

Logic:

How do we find several subsets possible?

If we think mathematically, the number of subsets possible is equal to the number of times a number is repeated.

Like in the first example, we have to take a vector as [1,2,3,3]

Here, 1 and 2 have only one time occurrence, but 3 has occurred 2 times, and the number of possible subsets is also 2.

Therefore, the number of possible subsets equals the most repeated element.

So, we need to determine the most repeated element from the entire vector.

Let us discuss the code now:

First, we need to take input for vector size and vector elements:

The above lines of code will take the vector size as input and then take the vector elements as input.

Now, we need to find out the maximum frequency of repeating elements and the number of times an element has repeated the entire vector.

So, for every element, we need to find out the frequency. To find the frequency for every element in the vector, we search the entire vector except the same indexed element and find the frequency of every element.

This part of the code will determine the frequency of every vector element. While finding the frequency of the vector, we will be storing the frequency in a variable called m, and we know that we should find the maximum frequency of the entire array, so it is handled by ans=max(ans,m), this will help in storing the maximum frequency.

Finally, after every element frequency is found, the maximum will be stored in the ans variable, and finally, we will print it.

Here, there is a case where we need to handle, i.e., when we have no repeating elements; in this case, the value in the ans variable will be stored as 1; when ans is 1, we will print as " No Need to divide the vector elements all elements are distinct".

Otherwise, we will print the number of subsets required to distinguish the vector elements.

The above part of the code will handle print if no repeating elements are there and if they exist.

Let us discuss the time and space complexity of this code:

Time complexity: If we ignore the time taken to take the input, the time is consumed for finding the frequency of every element in the vector.

For every element in the vector, we have to search for the entire vector, so the time taken will be O(N*2)

Space complexity:

In this code, we have not used any space, so in this code, it takes a constant amount of space, i.e., O(1).

In the previous approach, the time taken is O(N*2), but we need to reduce the time complexity of the code.

To reduce the time complexity of the code, we will be using maps since the maps can store two variables, one for the element and another for a count of the element.

For the above problem, we need the count of every element, so using a map is the perfect approach.

So, let us implement the code using the map.

CODE:

Output:

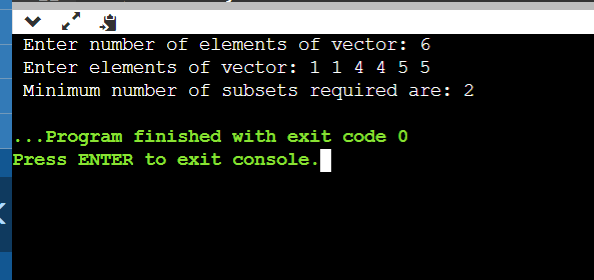
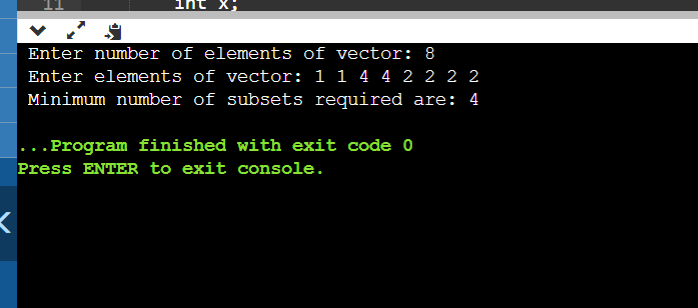
EXPLANATION:

First, we need to take the input for vector size and vector elements as input from the user and also push the elements of the vector into the map, where the count will be stored in the second variable of every map element.

The above lines of code will take the input of vector size and elements of a vector; while taking the input, we will also store the values in the map. If the element is not present in the map, a new one will be added. The frequency of the element will be increased.

Now, we need to find the maximum frequency of all the elements of the map, so to find it, we need to traverse along the map and do it by using a for loop.

The above part of the code will find the maximum frequency of any occurring element.

If the frequency or ans is 1, it indicates that all the elements are distinct, so there is no need to make the subsets.

The above part of the code will print the minimum number of subsets required to be done. If there is no need to make subsets, the condition is satisfied, and the below statement is printed; otherwise, the statement under else will be printed.

Let us discuss the time and space complexity of the code:

Time complexity: If we ignore the time taken to take the input, then we traverse along the map to find the maximum count value, and the maximum possible length of the map can be N so that the time complexity will be O(N)

Space complexity: Here, we used the map to store the elements of the vector, and in the worst-case map, we also took N space to store the elements of the vector, so space complexity is O(N).

Tabular representation of approaches: